ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
R. Rajeswari 1, G. Gunasekaran 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
Tumor is an abnormal mass of tissue which may be solid or fluid. Tumor is a collection of cells forming a lump or mass. The tumor is of different types and they have different characteristics and different treatment. This tumor, when turns in to cancer become life-threatening. So medical imaging, it is necessary to detect the exact location of tumor and its type. For locating tumor in magnetic resonance image (MRI) segmentation of MRI plays an important role.MRI is the preferred technology which enables the diagnosis and evaluation of brain tumor. The current work presents a Watershed method for tumor segmentation and hierarchical clustering algorithm that is employed to cluster brain tumor. Comparing to the other clustering techniques the performance of hierarchical clustering plays a major role. The patient's stage is determined by this process, whether it can be cured with medicine or not
KEYWORDS |
| Tumor, MRI Scan, Watershed, Clustering, Hierarchical Clustering. |
I. INTRODUCTION |
| A tumor may be primary or secondary. If it is the origin, then it is known as primary. If the part of the tumor spreads to another place and grows on its own, then it is known as secondary. The brain tumor affects CSF (Cerebral Spinal Fluid) and causes strokes. The physician gives the treatment for the strokes rather than the treatment for tumors. So the detection of the tumor is important for that treatment. The life expectancy of the person affected by the brain tumor will increase if it is detected at an earlier stage. Normally tumor cells are of two types Mass and Malignant. The detection of the malignant tumor is somewhat difficult to mass tumor. For the accurate recognition of the malignant a 3-D representation of brain and 3-D analyzer tool is required. This paper focuses on the detection of mass tumor. The development platform for the detection is mat lab because it is easy to develop and execute. At the end, we are providing systems that detect the tumor and its shape [1]. |
a) Types of Tumor |
| Brain tumors are classified based on the type of tissue involved, the location of the tumor, whether it is benign or malignant. |
ïÃâ÷ Benign brain tumor |
| This type of tumor generally do not consist cancer cells and can be removed. Benign brain tumors usually have an obvious border or edge. They don’t spread to other parts of the body. However, benign tumors can cause serious health problems. |
ïÃâ÷ Malignant brain tumor |
| This consists of cancer cells and hence also called as brain cancer. They are likely to grow rapidly and can affect nearby healthy brain tissues. This type of tumor can be a threat for life. Now, depending on what is type of cell of tumor, doctor group brain tumors by grades. There are four grades as grade I to grade IV. Cells from low-grade tumors (grades I and II) look more normal and generally grow more slowly than cells from high-grade tumors (grades III and IV). Over time, a low-grade tumor may become a high grade tumor. |
b) Segmentation Techniques |
| Segmentation is the process which partitions an image into its constituent regions or objects. Image segmentation is the first step in image analysis. The goal of image segmentation is to represent the image in the form which is meaningful and easier to analyze. Image segmentation divides an image into multiple parts and is typically used to identify objects or other relevant information in digital images. The most basic and important technique in image processing is image segmentation and it is necessary in pattern recognition. The basic idea behind segmentation is to segment an image into several clusters. The results of segmentation will be such that, it is possible to identify regions of interest and objects in the original image. Image segmentation is used in variety of applications including pattern recognition, object identification, feature extraction and medical imaging [4]. |
| There are number of segmentation techniques available in image processing. These techniques are explained in short below as in fig-1: |
| 1) Fuzzy C-Means Clustering |
| 2) K-Means Clustering |
| 3) Hierarchical clustering |
Stages of tumor detection |
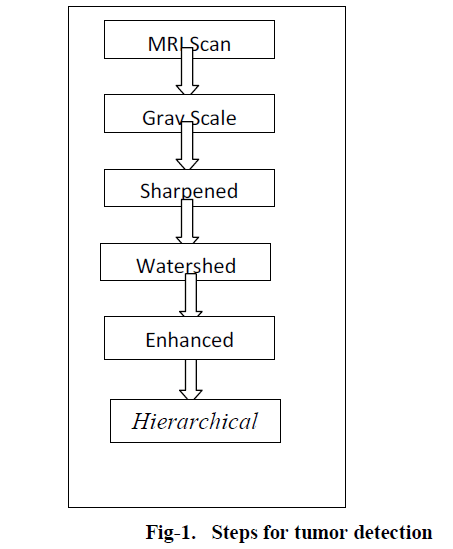 |
c) Magnetic Resonance Imaging (MRI) |
| MRI is basically used in the biomedical to detect and visualize finer details in the internal structure of the body. This technique is basically used to detect the differences in the tissues which have a far better technique as compared to computed tomography. So this makes this technique a very special one for the brain tumor detection and cancer imaging [2][3]. |
| This paper consist of, MRI image processing method which scans the tumor portion of brain. Compare to other method like CT (Computerized Tomography) and MRI (Magnetic Resonance Imaging) is the best method to view the tumor regions. Watershed algorithm is used to detect the tumor region from MRI scan report. In which these images are detected in the form of pixels, this method segments the tumor region. There are many different types of clustering algorithms have used to cluster the tumor region such as K-means clustering, Fuzzy C-means algorithm, Ant-Colony Optimization, where as Hierarchical clustering algorithm is signified in this paper to group the tumor regions in a single cluster. |
II. EXISTING METHODOLOGY |
| Clustering is the methodology which aims to group objects into subsets in such a fashion that similar objects are grouped together, while different objects belong to different groups. Clustering approach is widely used in biomedical applications particularly for brain tumor detection in abnormal magnetic resonance (MR) images. In the segmentation of medical images, the objective is to identify different regions, organs and anatomical structures from data acquired via MRI or other medical imaging technique. The following information is on existing clustering techniques used for tumor clusters. |
a) K-means Clustering |
| A cluster is a collection of objects which are similar between them and are dissimilar to the objects belonging to other clusters. Clustering is an unsupervised learning method which deals with finding a structure in a collection of unlabelled data. |
| The process of organizing objects into groups whose members are similar in some way. |
| K-means clustering is an algorithm to group objects based on attributes/features into k number of groups where k is a positive integer. The grouping (clustering) is done by minimizing the Euclidean distance between the data and the corresponding cluster centroid. Thus the function of k-means clustering is to cluster the data [5]. |
b) Fuzzy C-means Algorithm |
| The minimization of the c-means functional represents a nonlinear optimization problem that can be solved by using a variety of methods, including iterative minimization, simulated annealing or genetic algorithms. The most popular method is a simple Picard iteration through the first-order conditions for Stationary points, known as the fuzzy c-means (FCM) algorithm. The Stationary points of the objective function can be found by adjoining the constraint to J by means of Lagrange multipliers: |
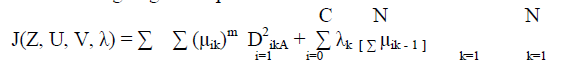 |
| The convergence of the FCM algorithm is proven in (Bezdek, 1980). Note that (4.8b) gives vi as the weighted mean of the data items that belong to a cluster, where the weights are the membership degrees. That is why the algorithm is called “c-means”. The fuzzy logic is a way of processing the data by giving the partial membership value to each pixel in the image. The membership value of the fuzzy set is ranges from 0 to 1. Fuzzy clustering is basically a multi valued logic that allows intermediate values member of one fuzzy set can also be members of other fuzzy sets in the same image. There is no abrupt transition between full membership and non-membership. The membership function defines the fuzziness of an image and also to define the information contained in the image. These are three main basic features involved in characterizing by membership function. They are supported Boundary. The core is a full member of the fuzzy set. The support is a non-membership value of the set and boundary is the intermediate or partial membership with value between 0 and 1 [6][7]. |
III. PROPOSED METHODOLOGY |
a) Watershed Segmentation |
| It is one of the best methods to group pixels of an image on the basis of their intensities. Pixels falling under similar intensities are grouped together. It is a good segmentation technique for dividing an image to separate a tumor from the image. Watershed is a mathematical morphological operating tool. Watershed is normally used for checking output rather than using as an input segmentation technique because it usually suffers from over segmentation and under segmentation. The watershed and thresholding algorithm techniques are useful for segmentation of brain tumor. Image segmentation is based on the division of the image into regions. Division is done on the basis of similar attributes. |
| Similarities are separated out into groups. Basic purpose of segmentation is the extraction of important features from the image, from which information can easily be perceived. The basic principle of watershed segmentation is to transform the gradient of a grey level image in a topographic surface, where the values of f (m, n) are interpreted as heights and each local minima embedded in an image is referred as catchments basins as shown in fig-2. |
| The Marker based Watershed Segmentation method possesses several important properties that makes it highly usable for various kinds of image segmentation problems. In the present method, the internal markers are produced from the gray scale image and then external markers are found by finding pixels that are exactly midway between the internal markers. |
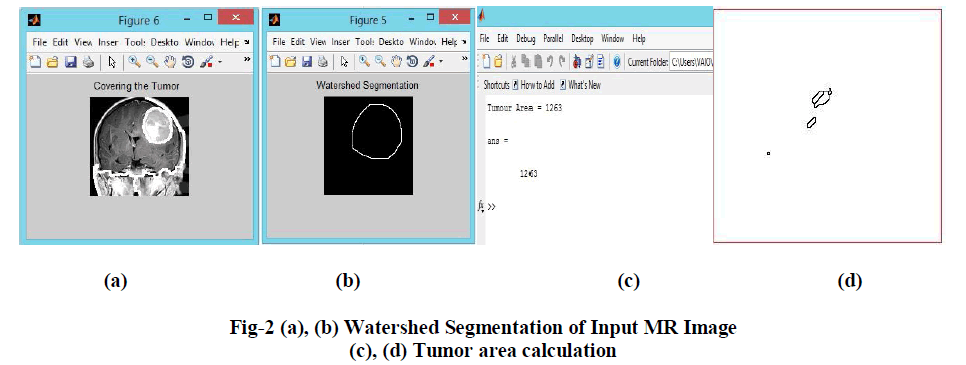 |
| This is done by computing the watershed transform of the distance transformed image. The gradient image is then modified by imposing regional minima at the location of both the internal and external markers. The next step involves the computation of the watershed transformation of the Marker modified gradient image to produce watershed ridge lines. Finally resulting watershed ridge lines are superimposed on the original image and produce the final segmentation of tumor region from MRI image process. |
b) Hierarchical Clustering Method |
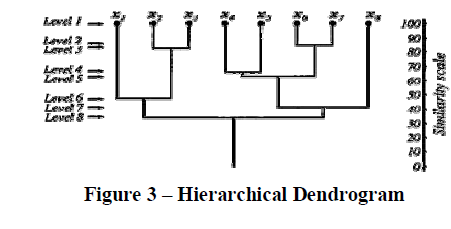
| There are many times when clusters have sub-classes within them, and which in turn have sub-classes of their own. Examples of such occurrences can be found in biological taxonomy when we have a species in the 'animal' kingdom, with a 'chordate' phylum, a sub-phylum of 'vertebrata, and so on. Such classifications are hierarchical and proper partitions can be found by the following classification methods. More formally, a sequence is said to be a hierarchical clustering if there exists 2 samples, c1 and c2, which belong in the same cluster at some level k and remain clustered together at all higher levels > k. One example of a hierarchical clustering is a correspondence tree, or a dendrogram (shown in Figure 3), which shows how samples are grouped together. The first level shows all samples xi as singleton clusters. As we increase levels, more and more samples are clustered together in a hierarchical manner. |
 |
| The hierarchical clustering procedures can be divided into two different approaches: agglomerative and divisive. The agglomerative approach to cluster analysis, used by the nearest and farthest Neighbour algorithms, is a bottom-up clumping approach where we begin with n singleton clusters and successively merge clusters to produce the other ones. The minimal spanning tree, on the other hand, uses the divisive approach which is a top-down approach where we start with one cluster and successively split clusters to produce others. |
| In general, all agglomerative algorithms usually yield the same results if the clusters are compact and well separated. However, if the clusters are close to one another or if their shapes are not hyper spherical, different results can be expected. The space and time complexities are O(n2) and O(cn2d2) respectively, where c is the number of clusters and d is the distance between them. |
 |
 |
| As a result, the nearest-neighbour algorithm can effectively detect elongated clusters but is not as effective when clusters are compact and of equal size. Therefore we look to the farthest-neighbour algorithm to detect such clusters. |
Algorithm: Farthest-Neighbour |
| The following is the farthest-neighbour clustering algorithm: |
| 1. begin |
| 2. initialize c; c' = n; Di = {xi}; i = 1,...,n |
| 3. do |
| 4. c' = c' - 1 |
| 5. Find nearest clusters Di and Dj |
| 6. Merge Di and Dj |
| 7. until c = c' |
| 8. return c clusters |
| 9. end |
| To find the nearest clusters in step 5, the following clustering criterion function is used: |
| dmax(Di, Dj) = max || x - x' ||, where x e Di and x' e Dj |
| Possible compromises between the two agglomerative approaches suggested above are to use the following criterion to find the nearest clusters: |
| davg(Di, Dj) = ( 1 / (ninj) ) S S || x - x' ||, where x e Di and x' e Dj |
| dmean(Di, Dj) = || mi - mj || |
Algorithm: Minimal Spanning Tree |
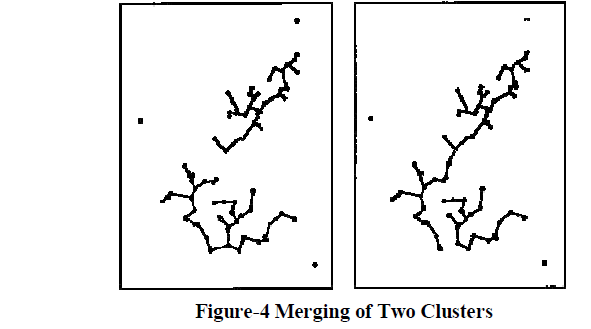
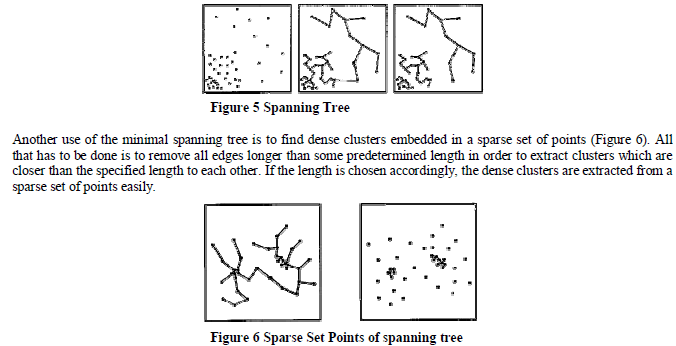
| The minimal spanning tree algorithm is a divisive approach because we are given the minimal spanning tree of all the nodes thus providing us with only one cluster to work with initially. There exists numerous ways to divide the clusters successively. One way is to simply remove the longest edge and create 2 clusters and then recursively removing the longest edge until the desired number of clusters is obtained. Another method in selecting which edge to remove is to compare the length of the edges to the lengths of the edges incident upon its nodes. As a result, we can consider an edge to be inconsistent if its length l is significantly larger than l', where l' is the average length of all other edges incident on its nodes (Figure 5). This method has the advantage of determining clusters which have different distances separating one another. |
 |
IV. EXPERIMENTAL RESULTS |
| In order to provide a more solid assessment for the proposed technique, this section discusses segmentation results obtained. The figures show the various stages obtained as a result of applying Hierarchical Multiple Markov Chain Model and TFR Segmentation Algorithm. |
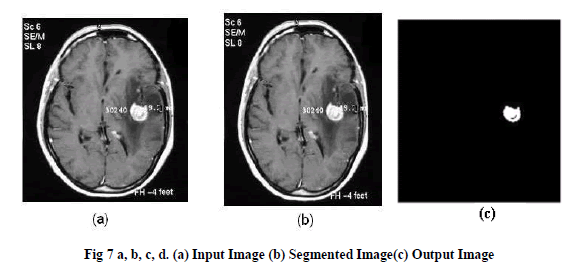 |
| Here, Hierarchical algorithm is applied as, a part of tumor region is cluster in single cluster and remaining similar objects or other similar clusters are grouped together to form a single cluster from the whole MR image as in fig-7. |
| Here, Hierarchical algorithm is applied as, a part of tumor region is cluster in single cluster and remaining similar objects or other similar clusters are grouped together to form a single cluster from the whole MR image as in fig-7. |
V. CONCLUSION |
| There are many simple greedy schemes for constructing hierarchical clustering’s the whole enterprise of hierarchical clustering could use some more justification. There always exists a hierarchical clustering which is close to optimal at every level of granularity, simultaneously. The k-clustering problem, minimize cost of the clustering. Our algorithm returns a hierarchical clustering such that for every k, the induced k-clustering is guaranteed to be within a factor eight of optimal. The standard heuristics for hierarchical clustering are greedy and work bottom-up |
| Single-linkage, average-linkage, complete-linkage, our algorithm is similar in efficiency and simplicity, but works topdown. In this paper tumor cell is grouped in to a single cluster and these single cluster is combined together to form another new cluster or these single cluster is sub divided in to multiple cluster based on the distance between the objects. |
| This paper describes Brain tumor detection using MRI image processing method, Segmentation by Using Watershed algorithm and the tumor cells are clustered using hierarchical clustering. Achieved results are shown in upper section which shows the efficient tumor detection by using hierarchical clustering algorithm. Shape and Size of tumor is described. |
References |
|