ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
| Edward E. Ogheneovo Lecturer I, Dept of Computer Science, University of Port Harcourt, Port Harcourt Nigeria. |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
Turing machines are the most powerful computational machines and are the theoretical basis for modern computers. Universal Turing machine works for all classes of languages including regular languages (Res), Context-free languages (CFLs), as well as recursively enumerable languages (RELs). In this paper, we discuss the concept of Universal Turing machine as a computing device that can be used for solving any problem that a computer or a human can solve. We show how the machine works in solving computational problems and design some algorithms showing to show the operational procedure of input symbols such as moving left, right, or stationary depending on the input symbol. Finally, we argue that the Universal Turing machine is a generalpurpose machine that can be used to compute any computable problem.
Keywords |
| Turing machines, Universal Turing machines, computation, computational model |
INTRODUCTION |
| Computation has been around for a very long time. Alan Turing and others (Alonzo Church, Markov, Emil Post, Stephen Kleene, etc.,) independently considered the problem of specifying a system in which computation could be defined and studied. Turing focused on human computation and thought about the way humans compute things by hand. With this examination of human computation, he designed a system in which computation could be expressed and carried out. According to him, any trivial computation requires the following: |
| ïÃâ÷ A simple sequence of computing instructions |
| ïÃâ÷ Scrath paper |
| ïÃâ÷ A device for writing and erasing |
| ïÃâ÷ A reading device |
| ïÃâ÷ The ability to remember which instruction is being carried out |
| Turing then developed a mathematical description of a device processing comprising all these attributes. This device is called Turing machine, which is today referred as a special purpose computer. Turing machines are simple abstract computational devices intended to help investigate the extent and limitations of what can be computed. Turing machines are the most powerful computational machines and are the theoretical basis for modern computers [13], [15]. They possess an infinite memory in the form of a tape, and a head which can read and change the tape, and move in either direction along the tape or remain stationary. Universal Turing Machine (UTM) works for all classes of languages including regular languages, Context Free Languages (CFLs) as well as Recursively Enumerable Languages (RELs) [2], [7], [9]. That is, these languages are all acceptable by Turing machines. |
| The key property of Turing machines and all other equivalent models of computations is universality: there exists a Turing machine, Tu, capable of simulating any other Turing machine. This machine is referred to as Universal Turing machines Tu. Thus a Universal Turing Machine, Tu can be thought of as a Turing machine interpreter, written in the language of Turing machines. This capability of self-referencing is the source of the versatility of Turing machines and other models of computation. Thus Tu can simulate an arbitrary Turing machine on arbitrary input. The universal machine achieves this by reading both the description of the machine to be simulated and the input from its own tape. This universality of Turing machine makes it possible for it to solve or compute any problem that a computer can also compute [18]. Hence, the name universal Turing machine. Alan Turing introduced this machine in 1937. |
| Turing machines are equivalent to algorithms, and are the theoretical basis for modern computers. Yet it is often very difficult to create and maintain Turing machines for all problems. Doing this will consume a large amount of memory space. Moreso, the creation of TMS for multiple tasks is very complex. This is the simple reason why a Universal Turing Machine (UTM) was designed. This Universal Turing machine is a machine that is able to simulate any other Turing machine, thus providing a single model and solution for all the computational problems [17]. A UTM is the abstract model for all computational models. A UTM (Tu) is an automation that, given as input the description of any Turing machine Tm, and a string, ïÿýïÿý, can simulate the computation of Tm on ïÿýïÿý. It reduces the memory usage when compared to using multiple TMs. |
| The transition function is the core part of a Universal Turing Machine. The UTM (Tu) works on the basis of the rules defined in it. The transition function ïÃÂó for a Tu with single tape is defined as: |
 |
| A UTM can solve any problem that can be solved using a FSA, PDA or even a Standard Turing Machine ( ). |
II. RELATED WORK |
| Jarvis and Lucas [10] implemented a Universal Turing Machine for the JFLAP platform. JFLAP is most successful and widely used tool for visualizing and simulating automata such as finite state machines, pushdown automata, and Turing Machines. They used JFLAP to simulate the Universal Turing Machine. Using their system, a user can get a direct and interactive experience of how this Turing Machine is capable of emulating other Turing Machines. This Universal Turing machine does not alter the portion of its memory that contains the list-of-final states of Tm and the list-of-transitions. Sumitha and Geddam [18] describes the implementation of Recursively Enumerable Languages (RELs) [8] using the Universal Turing machine for JFLAP platform. JFLAP is the most successful and widely used tool for visualizing and simulating all types of automata. They used the JFLAP to simulate many Turing machines and provide a single model and solution for all the computational problems. |
| Maheshwari and Dorairangaswamy [14] implement context-free languages in Universal Turing machines (UTMs) using JFLAP tool. They use JFLAP to simulate Turing machines to function as a UTM that acts as a single model and solution for all computational problems. Eberbach [6] proposed an evolutionary computation machine using a formal model of evolutionary computation. It investigated the convergence and convergence rate and provided sufficient conditions needed for the completeness and optimality of evolutionary search with particular reference to total optimality as an instance of the multi-objective optimization of the Universal Evolutionary Turing machine. The model was able to solve non-algorithmically the halting problem. |
III. COMPUTATIONAL PROBLEMS |
| Computation is often defined formally using the mathematical concept of a Turing machine, a kind of computation whose operation is simple enough to be described with great precision. Such a machine needs to be powerful enough to perform any computation that a computer can, and Turing machines are known to be able to carry out any computation that current computers are capable of. Computation is any process that can be carried out by a computer [4]. It must be noted that computation as used here does not mean mathematical calculation such as the computation of the product of two numbers or the logarithm of a number. Computation as used here simply means includes all kinds of computer operations, including data manipulation, information storage and retrieval, etc [1]. It involves machine readability. That is, for a language to be machine readable, it must have a simple structure to allow for effective translation. First, there must be an algorithm to translate a language, that is, a step-by-step process that is unambiguous and finite. Secondly, the algorithm must not be too complexity [12]. |
| Computable functions are functions that can be calculated using a mechanical calculation device given infinite amounts of time and storage space [3]. As stated earlier, Turing machines are very powerful. They can be used to compute any problem that is computable. That is, they can compute any problems that have effective procedure or algorithm that physical machine such as a computer can compute. Therefore, for a very large number of computational problems, it is possible to build a Turing machine that will be able to perform that computation. Turing’s original paper is on computable numbers. According to him, a number is Turing-computable if there exist a |
| Turing machine which starting from a blank tape computes an arbitrarily precise approximation to that number [17]. Thus Turing machines can do more than just writing-down numbers. They can therefore also be used for computing numeric functions and any other computable functions. |
| According to Church-Turing thesis, any function which has an algorithm is computable [19]. The concept of algorithm as used here signifies a step-by-step solution to a problem such as a function as demonstrated in algorithm 1 and algorithm 2. There are many models of computation that have been proposed for solving functions that are computable. These computational models are, however, equivalent in terms of their power to compute functions. These computation models are: |
| ïÃâ÷ Turing machines proposed by Alan Turing in 1936. |
| ïÃâ÷ Lambda (ïÃÂì) calculus proposed by Alonzo Church in 1936 |
| ïÃâ÷ Post machine proposed by Emil Post in 1952 |
| ïÃâ÷ Recursive function proposed by Stephen Kleene in 1952 |
| ïÃâ÷ Markov Model proposed by A. Markov in 1943 |
| ïÃâ÷ Register machines |
| Although these models use different representations for the functions, their inputs, outputs, and translations exist between any two models. Each computable function takes a fixed number of natural numbers as arguments. A function can be partial or total. A partial function is a function that is not defined for every possible choice of input [10, [16]. Thus a partial function is a function defined for a certain input and the resultant output is a single natural number. However, the output can be of interpreted as a list of numbers using functions that are paired. |
| It is possible to associate a partial function with each Turing machine. In this case, the input to the Turing machine is represented as an n-triple (e.g. X1, …, Xn). The integer represented by the maximal binary is separated by blank. This way, the Turing machine signs some bits or 0 if a blank is scanned when the machine halts. This is referred to as the output of the computation. This way, each Turing machine defines a partial function from n-tuples of integers onto the integers, n > 1. This type of function is said to be partial computable. However, for total computable functions, such functions are defined for all possible arguments. Thus, if the Turing machine halts for all inputs, then the function computed is defined for all arguments. |
| A function with the range (0, 1) is referred to as a predicate function. One major feature of a predicate function is that the predicate function has value TRUE or FALSE. The value is TRUE if the corresponding function has value 1 for some n-tuple of values for its arguments and is FALSE or undefined otherwise. For example, it is possible to design a Turing machine which when started on a tape representing a number terminates with TRUE on the tape if and only if the argument is a 1. Thus a Turing computable functions are recursive functions. |
| Consider X as a binary string. Thus for functions |X|, it is possible to see. |
 |
IV. FUNCTION THAT CAN BE COMPUTED |
| In the previous section, we showed that some functions are computable. Apart from functions, there are other problems that can be computed by Turing machines. In this section, we further discuss these problems, Turing machines can be used to compute arithmetic on natural numbers, encoding Turing machines. According to Alan Turing, a number is Turing computable if there exists a Turing machine which starting from a blank tape computes an arbitrarily precise approximation to that number. Computable numbers are the real numbers that can be computed to any desired precision by a finite, terminating algorithm. Turing defines computable numbers as sequences of digits interpreted as decimal fractions between 0 and 1. In a similar fashion, Minsky [15] defines a computable number as a number for which there is a Turing machine which, given a on its initial tape, terminates with the nth digit of that number. |
| A closer look at Minsky’s definition shows that three important notions are worth noting: (1) that some n is specified at the start of the computation, (2) for any n the computation only takes a finite number of steps, after which the machine produces the desired result and then finally halt, and (3) that by using Turing machine, a finite definition in the form of machines table – is being used to define, what is potentially-infinite string of decimal digits. |
| Formally, we define a computable number as a real number a such that if it can be approximated by some function given any integer n, the function produces an integer are such there: |
 |
| Therefore, a real number is computable if and only if there is a computable Dedekind cut D converging to it. The function D is unique for each irrational computable number. Finally, a complex number is said to be computable if its real and imaginary parts are computable. |
V. CHARACTERISTICS OF COMPUTABLE FUNCTIONS |
| As stated earlier, every computable function must have an algorithm showing the step-by-step procedure of how a function can be computed. However, as seen earlier, many models of computation have been developed ranging from Turing machines ïÿýïÿý–recursive functions, Lambda calculus, and a host of others. However, one interesting thing about these models is that even though they differ in their properties, they all give equivalent classes of computable functions in that they are all capable of solving the same problems. Thus every procedure or algorithm for computing a computable function has the following characteristics according to [5], [20]. |
| i. There must be instructions (i.e. a program) finite in length, for the algorithm. The implication is that every computable function must have an algorithm that completely describes how the function is to be computed. |
| ii. If the algorithm is given a k-tuple x in the domain (i.e. set of all inputs for which the function is defined) of f, then after a finite number of discrete steps the procedure must terminate and produce f(x). |
| iii. If the procedure is given a k-tuple x which is not in the domain of f, then the procedure might go on forever, never halting; or it might get stuck at some point, but it must not pretend to produce a value for f at x. Thus if a value for f (x) is ever found, it must be the correct value. |
VI. THE UNIVERSAL TURING MACHINE |
| The UTM has a tape infinite in both ends to hold the input and perform the computation. It also has a read/write head to position the input symbol an infinite memory [9], [11]. There are two other tapes also that are used for the processing. The first tape holds the description of the original Turing machine Tm, and the other tape holds the internal state of Tm. |
| The input to the UTM, Tu, is given in the form <Tm, ω> where Tm is the Turing machine that is to be manipulated and ïÿýïÿý is an input string for Tm. The execution of the Turing machine is specified by transition rules or delta rules. Each transition is of the form: |
| ïÃÂä (qi, a) = (qj, b, R) |
| where qi = the initial state |
| a = the current read symbol |
| qj = the next state final state |
| b = the write symbol |
| R = the direction to which the tape head has to move (i.e., left or right) |
| The tape head of the Turing machine and that of the UTM can move in either direct, move left specified by L or move right specified by R. The tape head can also decide to stay in its current position, this is specified by S. The encoded input is given to the UTM. The tape head scans the contents of the tape and reads the current input symbol and the current internal state. It checks the transition rules stored in the description tape and performs the operation as specified in the transition rule of the original Tm. When all the input symbols have been scanned, the Tu enters the final state, check section and performs the same as Tm. The internal structure of universal Turing machine is shown in the figure 1. |
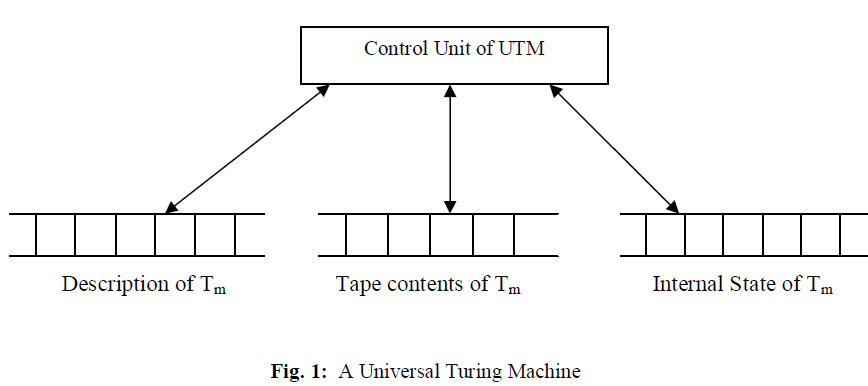 |
VII. UNIVERSAL TURING MACHINE’S ALGORITHM |
| Algorithm 1 shows the initialization of universal Turing machine. The algorithm is designed using the structured programming approach such as in Pascal programming language using the while , for and repeat until loops as the control structures. |
 |
| The next algorithm, algorithm 2 is used for the main loop of the universal Turing machine as defined in the initialization algorithm 1. The algorithm shows the operation of Turing machine in terms of moving the input symbol left, right, or stay positional until the last input symbol is reached. |
| Algorithm2: Universal Turing machine, main loop. |
 |
 |
| Algorithm 2 is used for the main loop of the universal Turing machine as defined in the initialization algorithm 1. The algorithm shows the operation of Turing machine in terms of moving the input symbol left, right, or stay positional until the last input symbol is reached. The algorithm describes the iterative simulation of universal Turing machine, Tu. The Tu starts reading the input symbol from the leftmost position of the of the tape content from a nonblank position. The tape header checks if there is any input symbol. If there is none, the machine halts. However, if the input symbol matches, the iteration process is repeated and the machine moves the tape header to the right until the end of the file and finally halts. The process is repeated two more times but this time around using the “yes” or “no” options in place of “halts”. The tape header the moves back to the left edge of the description tape and the state tape. This process is repeated until there are not more input symbols left and until reaching âÃÅ Ãâ on description tape. |
VIII. CONCLUSION |
| In this paper, we have discussed the concept of Universal Turing machine and how it can be used to solve any problem that a computer can solve or any problem that is computable. Computable functions are functions that can be calculated using a mechanical calculation device given infinite amounts of time and storage space. As stated earlier, Turing machines are very powerful. They can be used to compute any problem that is computable. That is, they can compute any problems that have effective procedure or algorithm that physical machine such as a computer can compute. Therefore, for a very large number of computational problems, it is possible to build a Turing machine that will be able to perform that computation. Turing’s original paper is on computable numbers. Thus Turing machines can do more than just writing-down numbers. They can therefore also be used for computing numeric functions and any other computable function. The key property of Turing machines and all other equivalent models of computations is universality: there exists a Turing machine, Tu, capable of simulating any other Turing machine. This machine is referred to as Universal Turing machines Tu. Thus a Universal Turing Machine, Tu can be thought of as a Turing machine interpreter, written in the language of Turing machines. This capability of self-referencing is the source of the versatility of Turing machines and other models of computation. Thus Tu can simulate an arbitrary Turing machine on arbitrary input. The universal machine achieves this by reading both the description of the machine to be simulated and the input from its own tape. This universality of Turing machine makes it possible for it to solve or compute any problem that a computer can also compute. |
References |
|