ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
| Mr.K.ANANDAN1 and Mr.N.S.YOGAANANTH2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
FIR digital filters are used in Digital Signal Processing (DSP) by the virtue of its, linear phase, fewer finite precision error, stability and efficient implementation. This paper presents an architectural approach to the design of High speed reconfigurable finite impulse response (FIR) filter. In this paper new reconfigurable low power FIR filter architecture using Multiplier Control Decision Window(MCSD) is proposed. The approach is well suited when the filter order is fixed and not changed for particular applications, and efficient trade-off between power savings and filter performance can be made using the proposed architecture. Thus the proposed architecture offers 20% power efficiency and 40% delay reduction compared to the best existing reconfigurable FIR filter. This has been implemented and tested on Spartan-3 xc3s200- 5pq208 field-programmable gate array (FPGA).
Keywords |
| FIR filter architecture, Multiplier Control Decision Window(MCSD), Reconfigurability |
I. INTRODUCTION |
| The explosive growth in mobile computing and portable multimedia applications has increased the demand for low power digital signal processing (DSP) systems. One of the most widely used operations performed in DSP is finite impulse response (FIR) filtering. The input-output relationship of the linear time invariant (LTI) FIR filter can be expressed as the following equation(1): |
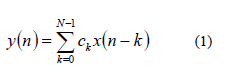 |
| Where N represents the length of FIR filter, ck the coefficient, and the x(n-k) input data at time instant. In many applications, in order to achieve high spectral containment and/or noise attenuation, FIR filters with fairly large number of taps are necessary. Many previous efforts for reducing power consumption of FIR filter generally focus on the optimization of the filter coefficients while maintaining a fixed filter order. In those approaches, FIR filter structures are simplified to add and shift operations, and minimizing the number of additions/subtractions is one of the main goals of the research. However, one of the drawbacks encountered in those approaches is that once the filter architecture is decided, the coefficients cannot be changed; therefore, those techniques are not applicable to the FIR filter with programmable coefficients |
II. TRANSPOSED DIRECT FORM OF AN FIR FILTER |
| As shown in Fig. 1[1], FIR filtering operation performs the weighted summations of input sequences, called as convolution sum, which are frequently used to implement the frequency selective low-pass, high-pass, or band-pass filters .Generally, since the amount of computation and the corresponding power consumption of FIR filter are directly proportional to the filter order, if we can dynamically change the filter order by turning off some of multipliers, significant power savings can be achieved. However, performance degradation should be carefully considered when we change the filter order. |
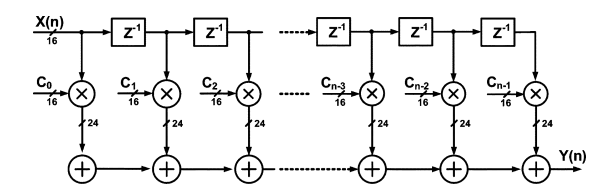 |
| Fig 1: Transposed direct form of an FIR filter |
| In the fixed point arithmetic of FIR filter, full operand bit-widths of the multiplier outputs is not generally used. In otherwords, as shown in Fig. 1, when the bit-widths of data inputs and coefficients are 16, the multiplier generates 32-bit outputs .However, considering the circuit area of the following adders, the LSBs of multipliers outputs are usually truncated or rounded off, (e.g., 24 bits are used in Fig. 1) which incurs quantization errors. When we turn off the multiplier in the FIR filter, if we can carefully select the input and coefficient amplitudes such that the multiplication of those two numbers is as small as the quantization error, filter performance degradation can be made negligible . By threshold, we mean that when the filter input and coefficient are smaller than and , respectively, the multiplication is canceled in the filtering operation. When we determine the trade-off between filter performance and power savings should be carefully considered. |
III. ARCHITECTURE OF PROPOSED RECONFIGURABLE FIR FILTER |
| In this section[1], we present a direct form (DF) architecture of the reconfigurable FIR filter, which is shown in Fig. 2(a). In order to monitor the amplitudes of input samples and cancel the right multiplication operations, amplitude detector (AD) in Fig. 2(b) is used. When the absolute value of x(n) is smaller than the threshold , the output of AD is set to “1”. The design of AD is dependent on the input threshold, where the fan-in’s of AND and OR gate are decided by a simple comparator. In the proposed reconfigurable filter, if we turn off the multiplier by considering each of the input amplitude only, then if the amplitude of input abruptly changes for every cycle, the multiplier will be turned on and off continuously, which incurs considerable switching activities. Multiplier control signal decision window (MCSD) in Fig. 2(a) is used to solve the switching problem. Using ctrl signal generator inside MCSD, the number of input samples consecutively smaller than threshold are counted and the multipliers are turned off only when consecutive input samples are smaller than threshold. As an input smaller than threshold comes in and AD output is set to “1”, the counter is counting up. When the counter reaches, the ctrl signal in the figure changes to “1”, which indicates that consecutive small inputs are monitored and the multipliers are ready to turn off. One additional bit, in Fig. 2(a), is added and it is controlled by ctrl. The accompanies with input data all the way in the following flip-flops to indicate that the input sample is smaller than threshold and the multiplication can be canceled when the coefficient of the corresponding multiplier is also smaller than threshold. Once the signal is set inside MCSD, the signal does not change outside MCSD and holds the amplitude information of the input. A delay component is added in front of the first tap for the synchronization between and in Fig. 2(a) since one clock pulse is needed due to the counter in MCSD. In case of adaptive filters, additional ADs for monitoring the coefficient amplitudes are required as shown in Fig. 2(a). However, in the FIR filter with fixed or programmable coefficients, since we know the amplitude of coefficients ahead, extra AD modules for coefficient monitoring are not needed. When the amplitudes of input and coefficient are smaller than threshold, the multiplier is turned off by setting signal [Fig. 2(a)] to “1”. The area overheads of the proposed reconfigurable filter are flip-flops for signals, AD and ctrl signal generator in-side MCSD and the modified gates for turning off multipliers. Those overheads can be implemented using simple logic gates, and a single AD is needed for input monitoring as specified in Fig. 2(a). Consequently, the overall circuit overhead for implementing reconfigurable filter is as small as a single multiplier. In the proposed architecture, go for Vedic multiplier from normal multiplier shown in fig.3 for getting better power and speed |
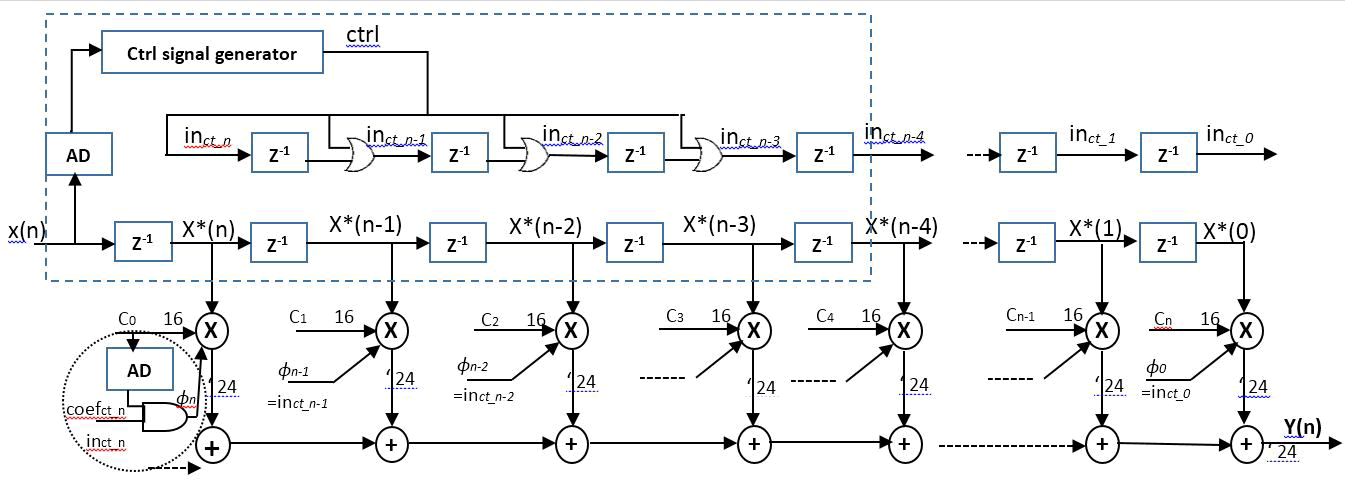 |
| (a) |
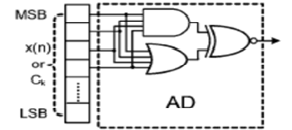 |
| (b) |
| Fig.2. (a)Proposed Reconfigurable fir filter (b)Amplitude Detection Logic(AD). |
| By using the high speed multipliers, Such as booth’s multiplier and vedic multiplier the performance of the reconfigurable FIR filter is increased without any degradation |
IV. VEDIC MULTIPLIER |
| The 16X16 bit multiplier structured using 8X8 bits blocks as shown in Figure 3. In this Figure.3 the 16 bit multiplicand A can be decomposed into pair of 8 bits AH-AL. Similarly multiplicand B can be decomposed into BH-BL. The outputs of 8X8 bit multipliers are added accordingly to obtain the 32 bits final product. |
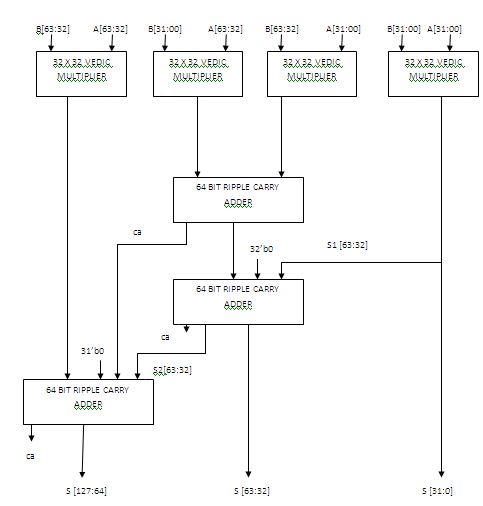 |
| Fig.3.Vedic Multiplier |
V. SIMULATION RESULTS |
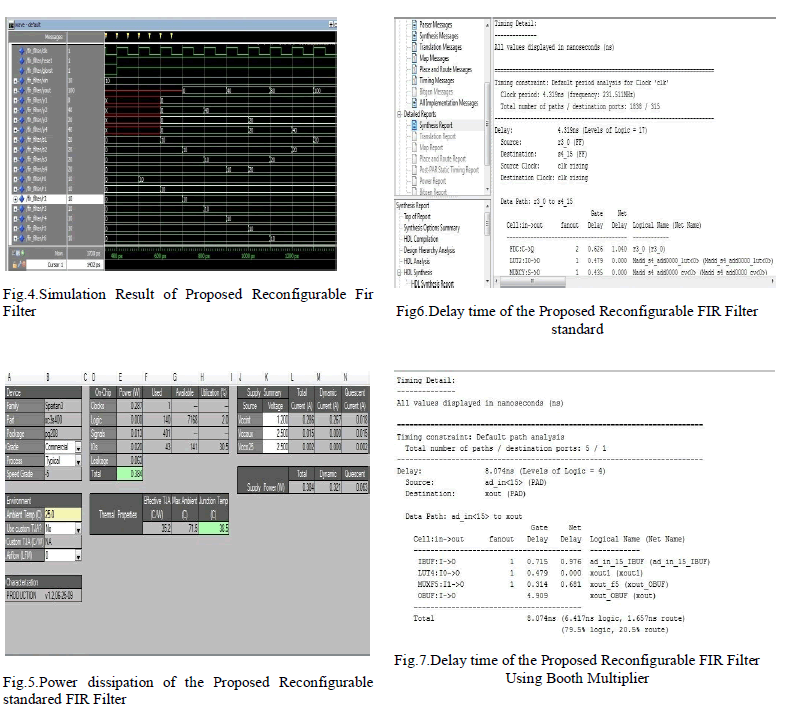
| The results presented establish a clear area advantage of Proposed FIR architecture over prior architecture for typical filter parameters with comparable maximum clock rates. MSCD architecture achieved high clock frequency compared to direct form architecture, Due to logic depth high in direct form it will less speed, but in our proposed architecture gives high speed and low power . We validated our techniques on Spartan-III devices where we observed significant area and power reductions over traditional Distributed Arithmetic based techniques and multiplierless technique. |
 |
 |
VI. CONCLUSION |
| The proposed new approaches namely, MSCD for implementing reconfigurable higher order filters for low power. A low power reconfigurable FIR filter architecture is designed to allow efficient trade-off between the filter performance and computation energy. The MSCD architecture results in high speed filters and low power filter implementations. The MSCD provides the flexibility of changing the filter coefficient word lengths dynamically. We have implemented the architectures on Spartan-III XC3S200-5PQ-208 FPGA and synthesized. |
| The proposed reconfigurable architectures achieve High speed and low power. |
References |
|