Research & Reviews: Journal of Engineering and Technology
MenuISSN: 2319-9873
ISSN: 2319-9873
+44 7456 035580 National Polytechnic School of Oran Maurice Audin, Oran, Algeria
Received Date: 25/11/2017; Accepted Date: 28/01/2018; Published Date: 28/02/2018
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
This paper presents an improved five-level direct torque control (DTC) with 36 sectors of induction motor (IM) based on fuzzy logic. This intelligent technique was used to replace, on the one hand the hysteresis comparators in order to reduce THD (Total Harmonic Distortion) of stator current, torque ripple and stator flux ripple, on other hand and the classic integral proportional (PI) in order to increase the response time period of the system, to optimize the performances of the closed loop control, and to adjust the parameters of the regulator to changes in the reference level. The validity of the proposed methods is confirmed by the simulation results.
Direct torque control, Induction motor, Fuzzy logic, Hysteresis comparators, PI, Total harmonic distortion
The induction motors have been widely used in many industrial and daily life applications such as pumps, fans and compressor due to its low cost, low maintenance, high robustness, simple construction and high efficiency. Nowadays, the induction motor drives have been able to be used in variable speed applications with the rapid development of power electronics [1].
A control literature review shows that a variety of solutions has been proposed for the control of induction motor systems. In the linear case, one has to mention the scalar control which is the first scheme proposed for this task. It is easy to implement but it does not provide good performance. The second well-known scheme is the vector control technique called also field oriented control (FOC) proposed by Blaschke. The main disadvantage of this later control technique is the inherent coupling of the speed sensor on the motor rotor shaft reduces its robustness [2]. The direct torque control (DTC) method has emerged as an alternative to Field Oriented Control (FOC) method for high performance AC drives since it was firstly proposed in the mid-1980 [3]. The main advantages of direct torque control are absence of coordinate transformation and current regulator. In this method, stator voltage vectors are selected according to the differences between the reference and actual torque and stator flux linkage [4]. The basic idea of this method is to use non-linear estimators of the torque and flux, making it possible to eliminate the controllers of the stator currents [5]. However, the main limit of conventional DTC scheme is high torque ripple, variable switching frequency, and the mean torque output, which does not match the torque demond. A variety of techniques have been proposed to overcome some of the drawbacks present in DTC. Some solution proposed are: DTC with space vector modulation (SVPWM), the use of a duty-ration controller to introduce a modulation between active vectors chosen from the look-up table and the zero vectors, use of artificial intelligence techniques. However the complexity of the control is considerably increased [6]. In the other hand, the utilization of multilevel inverter topology in the DTC system has gained popularity for the medium and high voltage applications. Typically, there are three types of multilevel inverters topologies. Those types are the neutral point clamped (NPC), flying capacitor (FC) and cascade H-bridge multilevel inverters (CHMI) [7]. In the other hand, multilevel inverters have the advantages of overcoming voltage limit capability of semiconductor switches, and improving, 2 harmonic profiles of output waveforms. The output voltage waveform approaches a sine wave, thus having practically no common-mode voltage and no voltage surge to the motor windings. Furthermore, the reduction in dv/dt can prevent motor windings and bearings from failure [8]. In this paper, a 5-level neutral point clamped multilevel inverter is used with look up table based DTC drive.
Common disadvantages of conventional DTC are high torque ripple, it also needs flux and torque estimators and therefore, accurate machine parameters are required. For that reason the application of artificial neural network and fuzzy logic control attracts the attention of many scientists from all over the world [9]. This paper is devoted to fuzzy logic direct torque control of sensorless IM fed by five-level diode clamped inverter.
In this paper two different DTC scheme will be compared with each other. These two schemes are conventional DTC with five-level NPC inverter, and five-level DTC with fuzzy logic controllers (fuzzy speed controller and fuzzy hysteresis comparators). The proposed scheme is described clearly and simulation results are reported to demonstrate its effectiveness. The proposed control scheme is implemented with Matlab.
The very first topology has switches at its neutral point to control the voltage levels. In 1980, Nabae and his friends modified this topology such that the neutral point voltage application to the output and neutral point voltage balance have been accomplished by diode pairs [10]. Figure 1 shows the circuit of a five-level diode clamped inverter and the switching states of each leg of the inverter. Each leg is composed of two upper and lower switches with anti-parallel diodes. It is composed by 24 pair’s transistor-diode. Every leg of this inverter includes eight pairs. Four series DC-link capacitors split the DC-bus voltage in half, and 18 clamping diodes confine the voltage across the switches within the voltage of the capacitors, each leg of the inverter can have five possible switching states; 4, 3, 2, 1, or 0.
Figure 1: Schematic diagram of a five-level inverter.
A five-level inverter can achieve 60 separate positions in the phase corresponding to the 61 sequences of the voltage inverter. The representation of the space voltage vectors of a five-level NPC inverter for all switching states is given by Figure 2.
Figure 2: Space vector diagram of five-level inverter.
Configuration of the basic DTC with five-level inverter is illustrated in Figure 3. In these control uses two hysteresis controllers for stator flux and developed torque, respectively. As the DTC control strategy is not based on mathematical analysis, it is not easy to give an apparent boundary to the division of torque error [11]. The reference frame related to the stator, makes possible to estimate flux and torque on the one hand and the position of flux stator on the other hand. The aim of the switches control is to give the vector representing the stator flux the direction determined by the reference value [12].
Figure 3: Conventional DTC control of IM drives.
The stator flux can be evaluated by integrating from the stator voltage equation:
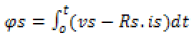(1)
The magnitude of the stator flux can be estimated by:
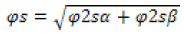(2)
The stator flux sector is determined by the components 
and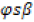 
. The angle between the referential and 
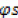is equal to:
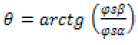(3)
Torque can be calculated using the components of the estimated flux and measured currents:
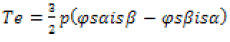(4)
The selection of the appropriate voltage vector is based on the switching table given in Table 1. The input quantities are the sector (N) and the digitized output variables Ccpl (torque hysteresis comparator) and Cflx (flux hysteresis comparator). Thus, the selection table generates pulses Sa, Sb, Sc to control the power switches in the five-level NPC inverter.
Table 1. Switching table for five-level DTC with 36 sectors.
| Cflx | ||||||
|---|---|---|---|---|---|---|
| 1 | 0 | |||||
| N | Ccpl | |||||
| 1 | 0 | -1 | 1 | 0 | -1 | |
| 1 | 14 | 2 | 54 | 24 | 32 | 44 |
| 2 | 15 | 2 | 55 | 25 | 32 | 45 |
| 3 | 18 | 2 | 58 | 28 | 32 | 48 |
| 4 | 18 | 7 | 58 | 28 | 37 | 48 |
| 5 | 20 | 7 | 60 | 30 | 37 | 50 |
| 6 | 24 | 7 | 4 | 34 | 37 | 54 |
| 7 | 24 | 12 | 4 | 34 | 42 | 54 |
| 8 | 25 | 12 | 5 | 35 | 42 | 55 |
| 9 | 28 | 12 | 8 | 38 | 42 | 58 |
| 10 | 28 | 17 | 8 | 38 | 47 | 58 |
| 11 | 30 | 17 | 10 | 40 | 47 | 60 |
| 12 | 34 | 17 | 14 | 44 | 47 | 4 |
| 13 | 34 | 22 | 14 | 44 | 52 | 4 |
| 14 | 35 | 22 | 15 | 45 | 52 | 5 |
| 15 | 38 | 22 | 18 | 48 | 52 | 8 |
| 16 | 38 | 27 | 18 | 48 | 57 | 8 |
| 17 | 40 | 27 | 20 | 50 | 57 | 10 |
| 18 | 44 | 27 | 24 | 54 | 57 | 14 |
| 19 | 44 | 32 | 24 | 54 | 2 | 14 |
| 20 | 45 | 32 | 25 | 55 | 2 | 15 |
| 21 | 48 | 32 | 28 | 58 | 2 | 18 |
| 22 | 48 | 37 | 28 | 58 | 7 | 18 |
| 23 | 50 | 37 | 30 | 60 | 7 | 20 |
| 24 | 54 | 37 | 34 | 4 | 7 | 24 |
| 25 | 54 | 42 | 34 | 4 | 12 | 24 |
| 26 | 55 | 42 | 35 | 5 | 12 | 25 |
| 27 | 58 | 42 | 38 | 8 | 12 | 28 |
| 28 | 58 | 47 | 38 | 8 | 17 | 28 |
| 29 | 60 | 47 | 40 | 10 | 17 | 30 |
| 30 | 4 | 47 | 44 | 14 | 17 | 34 |
| 31 | 4 | 52 | 44 | 14 | 22 | 34 |
| 32 | 5 | 52 | 45 | 15 | 22 | 35 |
| 33 | 8 | 52 | 48 | 18 | 22 | 38 |
| 34 | 8 | 57 | 48 | 18 | 27 | 38 |
| 35 | 10 | 57 | 50 | 20 | 27 | 40 |
| 36 | 14 | 57 | 54 | 24 | 27 | 44 |
Two-level stator flux and three-level torque hysteresis controllers are used according to the outputs of the torque and flux controllers Figure 4.
Figure 4: Hysteresis comparators.
The principle of five-level DTC with fuzzy controllers is similar to conventional DTC with five-level NPC inverter. The difference is using a fuzzy controller to replace the hysteresis comparators, and PI speed controller. As shown in Figure 5. The main objective of this study is the reduction of the THD value of stator current, electromagnetic torque ripples and stator flux ripples.
Figure 5: DTC control with fuzzy controllers.
In the objective to control the static error and to reduce the time response while preserving the system stability, the proportional integral corrector PI used is replaced with a fuzzy logic controller [13]. The fuzzy control is basically nonlinear and adaptive in nature, giving robust performance under parameter variation and load disturbance effet [14]. Fuzzy logic speed controller design is designed based on the human expert knowledge rule base. It does not require any mathematical model of the plant [15]. The fuzzy controller design is based on intuition and simulation. These values compose a training set which is used to obtain the table rules [11]. The block diagram of the fuzzy logic speed controller is shown in Figure 6. On possible initial rule base, that can be used in drive systems for a fuzzy logic controller, consist of 49 linguistic rules, as shown in Table 2 [16,17], and gives the change of the output of fuzzy logic controller in term of two input: the error (e=wref – w) and change of error (Δe).
Table 2. Fuzzy rules of speed.
| e | NL | NM | NP | EZ | PS | PM | PL |
|---|---|---|---|---|---|---|---|
| Δe | |||||||
| NL | NL | NL | NL | NL | NM | NP | EZ |
| NM | NL | NL | NL | NM | NP | EZ | PS |
| NP | NL | NL | NM | NP | EZ | PS | PM |
| EZ | NL | NM | NP | EZ | PS | PM | PL |
| PS | NM | NP | EZ | PSPM | PM | PL | PL |
| PM | NP | EZ | PS | PM | PL | PL | PL |
| PL | EZ | PS | PM | PL | PL | PL | PL |
Figure 6: Fuzzy logic speed controller.
Figures 7 and 8 show the membership functions of error and the change variables respectively.
Figure 7: Membership functions for error in speed.
Figure 8: Membership functions for change in error.
The Principe of the proposed fuzzy hysteresis comparators is to replace the two hysteresis comparators of torque and flux by the fuzzy logic. The block diagram for fuzzy based torque and stator flux hysteresis comparators is shown in Figures 9 and 10. The fuzzy controller design is based on intuition and simulation [18]. The fuzzy rules for the proposed hysteresis comparators are given in Table 2.
Figure 9: Fuzzy logic control of speed regulation.
Figure 10: Fuzzy logic control of speed regulation.
The induction motor used for the simulations has the following parameters: A 3-phase, 3 poles, Pn=1 MW; fs=60 Hz; Rs=0.228Ω; Rr=0.332Ω; Ls=0.0084H; Lr=0.0082H; Lm=0.0078H; J=20 kg.m2. To compare with conventional five-level DTC and five-level DTC with fuzzy controllers for IM drive are simulated. All Figs are the responses to step change load torque command from 0 to 6500 N.m. The results of simulation of conventional five-level DTC and five-level DTC with fuzzy logic controllers are shown in Figures 11 and 12 respectively.
Figure 11: Performances of five-level DTC for IM.
Figure 12: Performances of five-level DTC with fuzzy controllers for IM.
From the simulation results presented in Figures 11 and 12 it is apparent that the THD value of stator current for the fivelevel DTC with intelligent controllers (fuzzy speed controller and fuzzy hysteresis comparators) is considerably reduced. Table 3 shows the comparative analysis of THD value for stator current.
Table 3. Comparative analysis of THD value.
| Conventional DTC with five-level inverter | Five-level DTC with fuzzy controllers |
|---|---|
| 4.67% | 3.98% |
In the other hand, the dynamics of the components of the stator flux are not affected by the application of these load guidelines. Torque response comparing curves are shown in Figure 13. The torque ripple is significantly reduced when the fuzzy controllers is in use (Figure 13).
Figure 13: Zoom in the torque.
Figure 14 shows the flux responses of both the five-level DTC control and the five-level DTC with fuzzy controllers. It is found that the proposed variable band torque hysteresis and PI controller based DTC scheme exhibits smooth response and lesser ripple in flux as compared to the conventional five-level DTC scheme.
Figure 14: Zoom in the flux.
This paper presents a five-level DTC with 36 sectors for the IM with fuzzy controllers. This controllers determinates the desired amplitude of hysteresis comparators band and classical PI controller of speed. The proposed scheme was simulated and compared with conventional five-level DTC with 36 sectors using Matlab/Simulink. The five-level DTC with fuzzy controllers decreases considerably the torque ripples, stator flux ripples and THD value of stator current.