Index Terms
|
| Electric vehicle (EV), Ferrari’s method, interior permanent magnet synchronous motor (IPMSM), maximum torque per ampere (MTPA), torque control, voltage limit. |
INTRODUCTION
|
| AN interior permanent magnet synchronous motor (IPMSM) is known to be a superior solution in terms of efficiency, power density, and wide speed operating range. Because the reluctance torque can be utilized in the field-weakening region, the speed range of an IPMSM can be ex-tended while maintaining a constant power. This wide constant-power speed range gives the virtue of high power density. In an IPMSM, the torque is determined using not only the q-axis cur-rent iq , but also the d-axis current id . Therefore, there has been a question of optimality in combining the two current components. The solution is to produce the desired torque while minimizing the current magnitude. The maximum torque per ampere (MTPA), developed by Morimoto et al., is the cur-rent minimizing solution that is used under the base speed. Above the base speed, the MTPA is not feasible because of the limit in the dc-link voltage. In general, the optimal combination is found at the intersection of the torque and voltage limit curves. There are two problems that hinder pursuing the optimality in a practical situation: finding the intersection of the two curves is a highly nonlinear problem and the inductances change along with the current as a result of core saturation. Even crosscoupling phenomena cannot be neglected in some specific applications. |
| Thus, lookup table methods are widely used in the IPMSM torque control. They calculate the optimal current commands a priori, put them into a table, and then draw current commands from this table on the basis of the required torque and speed. |
| Nalepa and Kowalska effectively demonstrated the difficulty in finding the optimal solution owing to magnetic saturation and temperature variations. They proposed the use of a 3-D table in generating a feedforward compensation term for the d-axis current command based on the dc-link voltage, q-axis current, and speed. It should be noted that the field strength of a permanent magnet, for example a neodymium magnet, depends on the temperature, and its change cannot be neglected in electric vehicle (EV) applications because the ambient temperature is in the range of −40–150°C. Monajemy and Krishnan derived a fourth-order polynomial that resulted from torque and voltage limit equations and proposed the use of solution lookup tables based on flux linkage and torque commands. |
| Instead of using the lookup table, analytic approaches based on the mathematical model were attempted. However, those approaches were limited in practical use, because no explicit current set was obtainable from a given desired torque. Jeong et al. formulated current cost functions with torque and voltage constraints, and proposed the use of Newton’s method online to find the minimizing solutions. However, the convergence and computational burden would be problematic in real-time applications. Lee et al. Separated the cases on the basis of whether or not the solution was within the voltage limit and derived fourth-order polynomials in both cases. They found solutions by using a technique of approximating the fourth-order polynomial by a secondorder one. Bolognani proposed a local MTPA search method involving the injection of an additional pulsating current. Based on the magnitude of torque ripple, they constructed an MTPA-tracking loop. The torque ripple was measured indirectly via speed variation in the experiment |
| Direct torque control (DTC) for IPMSM drives has been investigated since the 1990s. DTC does not require an accurate motor model and parameters, except for the armature resistance. The torque and stator flux linkage are directly controlled using both a hysteresis comparator and a switching table [14], [15]. However, there are problems, such as an unfixed switching frequency and a large torque ripple. To solve these problems, space vector modulation was used, along with a reference flux vector calculator (RFVC) [16]. Relevant DTC methods that considered the voltage and current limits were followed. |
| For a surface-mounted permanent magnet synchronous mo-tor (SPMSM), selecting the optimal current set is simpler than for an IPMSM. Chen et al. [19] proposed a current controller for an SPMSM that adjusted the d-axis current on the basis of the voltage saturation. Because the current set was found on the voltage boundary, it was claimed to be optimal in the sense of minimizing the copper loss. Liu et al. [20] proposed an im-proved method of tracking the maximum torque per voltage line in an SPMSM by including the stator resistance and inverter nonlinearities. |
| In this paper, an online torque control method based on analytic solutions is proposed that covers the entire speed region. Fourth-order polynomials are derived from the optimality conditions. Two optimality conditions are considered: within the base speed region and in the fieldweakening region where the voltage limits is active. A discriminant is used to discern these two cases. Ferrari’s method is used to find the solution of quartic equations. |
| Through repeating the computations, variations in the d- and q -axes inductances are considered. This paper is organized as follows. Section II provides preliminaries on the IPMSM model, inductance saturation effect, and motor losses. In Section III, current minimizing conditions are derived with and without the voltage limit. Then, Ferrari’s method is used to solve quartic polynomials in Section IV, and a current minimizing algorithm is proposed in Section V. The entire torque control algorithm is constructed in Section VI. Finally, a simulation and some experiments are shown in Sections VII and VIII. |
PRELIMINARIES
|
| A. IPMSM Model and Voltage/Current Limits |
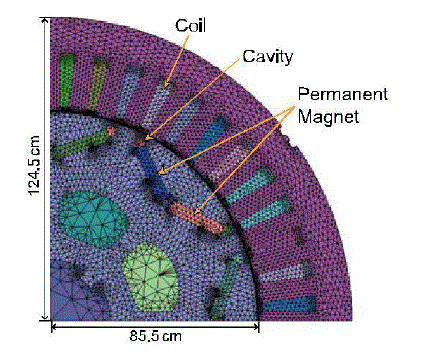
| Fig. 1 shows a 2-D FEM model of an IPMSM used in this experiment. The motor was developed as a propulsion motor for C-class passenger EVs. The outer diameters of stator and rotor are 249 and 171 mm, respectively. The stack length is 120 mm and the air-gap height is 0.8 mm. It has eight poles and two permanent magnets are arranged in a v-shape in each pole. Cavities were designed around the edges of permanent magnets to reduce the leakage flux. |
| Considering core saturation effects, the stator flux linkage of the IPMSM in the synchronous reference frame is described by |
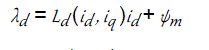 (1) (1) |
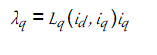 (2) (2) |
| where id and iq are the d- and q-axes currents; Ld and Lq are the d- and q-axes inductances; and ψm is the rotor flux linkage due to the permanent magnets. |
| The stator voltage equations of the IPMSM in the synchronous frame are |
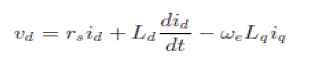 (3) (3) |
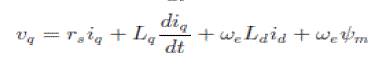 (4) (4) |
| where vd and vq are the d- and q-axes voltages; ωe is the electrical angular frequency; and rs is the stator resistance. The electromagnetic torque equation of the IPMSM is given by |
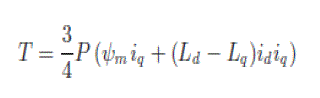 (5) (5) |
| (5) where P is the pole number. |
| Neglecting the ohmic drop across the stator resistance, the current and voltage limits are described by |
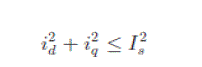 (6) (6) |
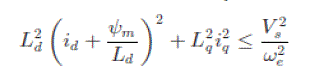 (7) (7) |
| where Is is the peak value of the maximum stator current and Vs is the peak value of the maximum phase voltage. |
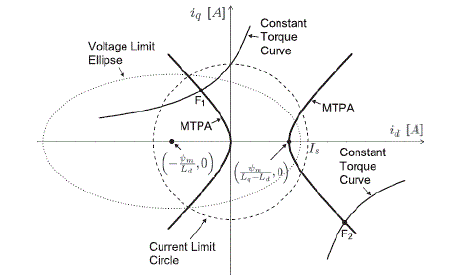
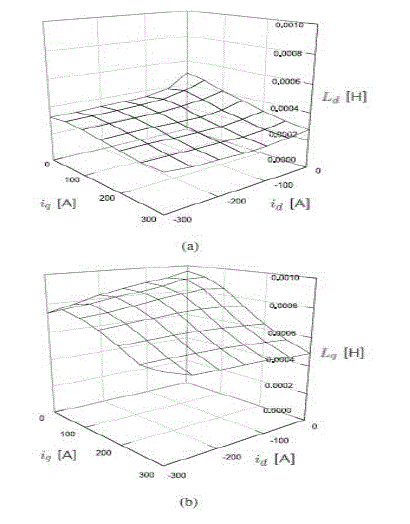
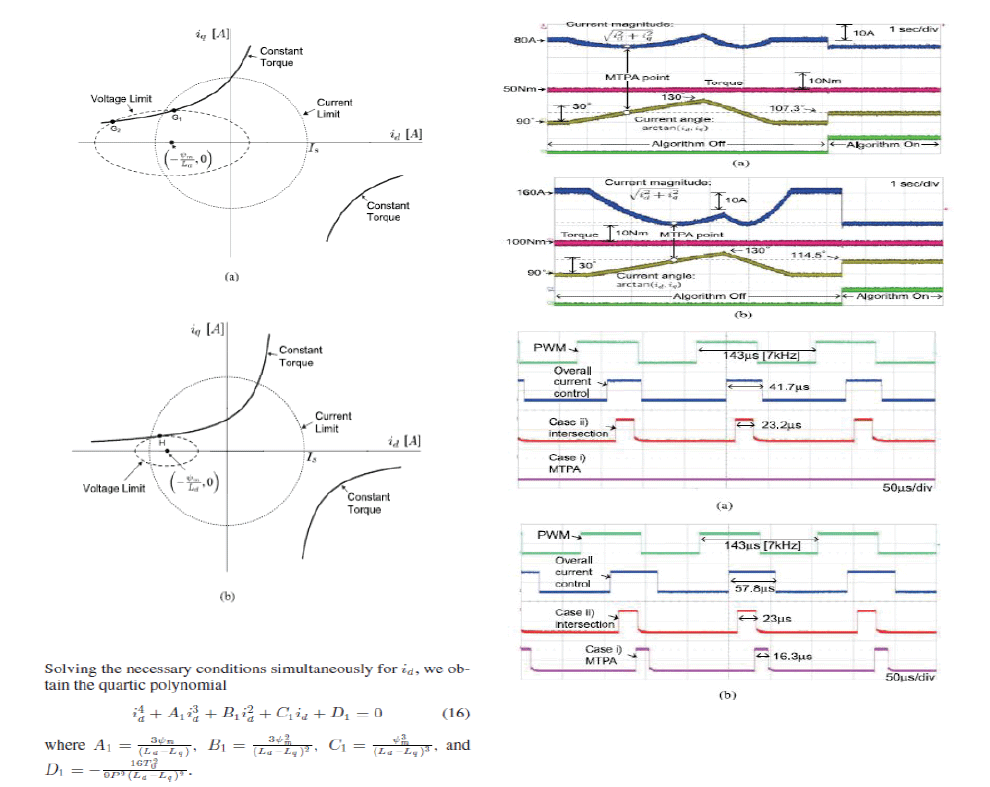
| As shown in Fig. 2, the current limit is the dashed circle centered at the origin with radius Is . The voltage limit appear as the dotted ellipse centered at (−ψ m , 0), and the major and minor radii are Vs /(Ld ωe ) and Vs /(Lq ωe ), respectively. Therefore, the voltage limit ellipse shrinks as ωe increases. |
| B. Inductance Change Due to the Core Saturation |
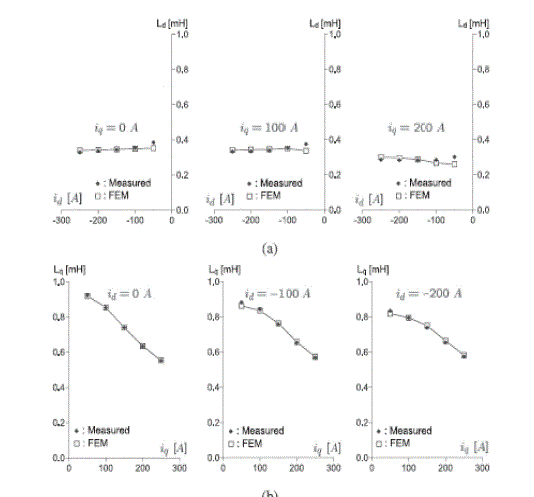
| In most torque control applications, torque sensors are not used directly. Instead, torque estimates based on the stator cur-rent measurements are used for feedback. Therefore, accurate inductance information is indispensable for a better torque precision and for an optimal current command selection. However, due to the core saturation, the inductances vary nonlinearly depending on the load condition and current |
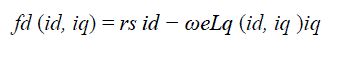 (8) (8) |
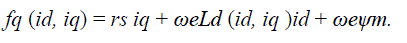 (9) (9) |
| Specifically, we measure the d- and q-axes voltages two times in the steady state, altering the polarity of the q-axis current, we measure fd (id, iq ), fd (id ,−iq ) and fq (id, iq ), fq (id ,−iq) under regulated current conditions, and estimate inductances in, |
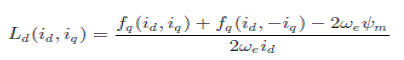 (10) (10) |
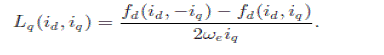 (11) (11) |
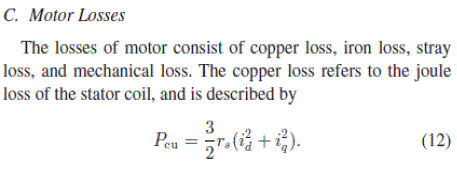 |
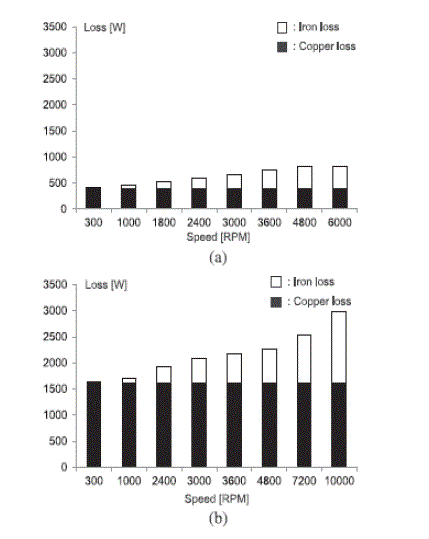
| In the extreme high speed range, the iron loss grows significantly. However, it is still smaller than the copper loss. |
| The mechanical and stray losses are small compared with the copper and iron losses. Fig. 5 shows copper and iron loss of the IPMSM used in this experiment To estimate inductances, we use voltage measurements To estimate inductances, we use voltage measurements The iron loss means the loss of the iron core for a timevarying field. It consists of two parts: hysteresis loss and eddy current loss. Since the loop area of a B–H curve signifies an energy per volume, the hysteresis loss is proportional to the frequency and the loop area. The loop area does not grow linearly with the maximum field Bm. Experimentally, it is estimated by khfBαm where kh = 40– 55 is a constant depending on the silicon contents in the steel, f is a frequency of the field, and α is in the range of 1.8–2.2 [22]. The latter is often called Joule loss, since it is caused by induced current in the conductive magnetic material. It is predicted analytically by kef2B2m , where ke is a constant which depends on the thickness of the steel lamination and the silicon percentage. Putting together, the iron loss under sinusoidal excitation is model |
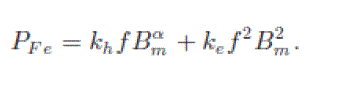 (13) (13) |
| The iron losses were calculated over a wide speed range under various current conditions using a commercial FEM tool, JMAG . The results state that copper loss is most dominant especially in the low-speed area. |
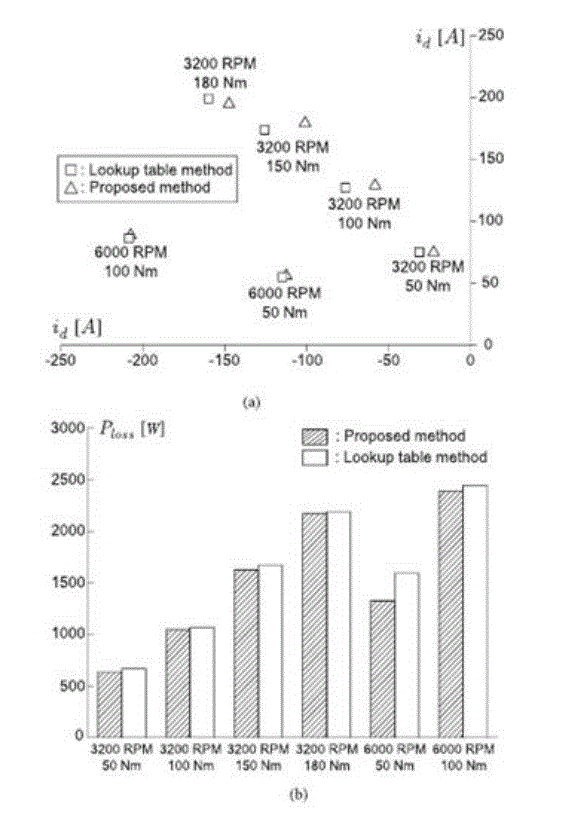
| Numerous research works were performed regarding the total loss minimization of an IPMSM. Morimoto et al. established a loss minimizing control based on an equivalent circuit which contained an iron loss model as well as a copper loss model. Utilizing a derivative of the loss function, a loss-minimizing d−axis current was determined. Cavallaro et al. developed an online loss minimizing algorithm based on the loss model of Morimoto. Lee et al. proposed a method of finding the loss minimizing solution using an approximation technique. |
| The total loss minimization is not an easy task because a target cost function itself is a high-order polynomial if an iron loss model is included. Furthermore, the coefficients vary depending on current and frequency [25]. Thereby, an explicit form of analytical solutions is hardly obtainable. Furthermore, the computational load should not be high for practical applications. In this study, we narrow down the focus to the copper loss minimization like the MTPA. But we consider voltage and current limits, while accepting inductance variations. |
ANALYTIC SOLUTION FOR CURRENT MINIMIZATION
|
| In order to establish a torque control loop, it is necessary to find the current command values, (i* d, i*q ). There are numerous (id, iq ) choices for a given torque, as shown in Fig. 2. However, each choice needs to be evaluated from the perspective of loss minimization. It should be noted that the winding copper loss is the dominant one among many loss components. Thus, a simple optimization method is to focus on just reducing the stator current, and the MTPA is such a current minimizing solution. |
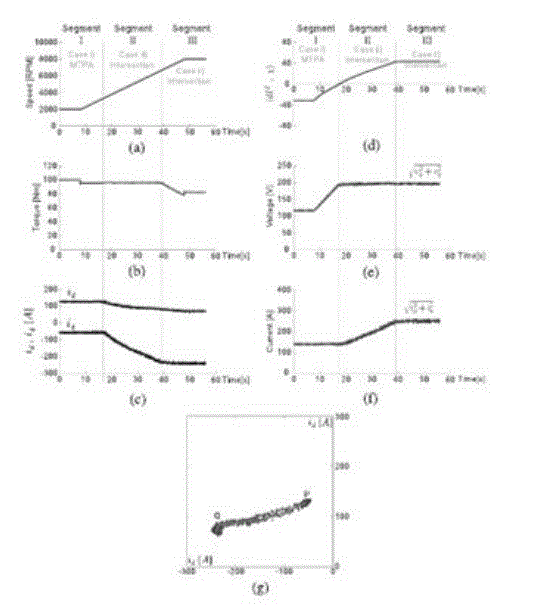
| If a torque curve intersects the MTPA line within the voltage and current limits, then the intersection point will be a desired current command. However, the MTPA solution may be located outside the voltage limit, as shown in Fig. 6. In such cases, a suboptimal solution is found at the intersection between the torque curve and the voltage limit ellipse. |
FERRARI’S SOLUTION TO QUARTIC EQUATIONS
|
| In the above, two quartic polynomials are derived: from either the MTPA or the voltage limit. It is known that a general solution always exists for quartic polynomials. Lodovico Ferrari invented a systematic procedure to solve all quartics. In this section, analytic solutions are obtained utilizing Ferrari’s method |
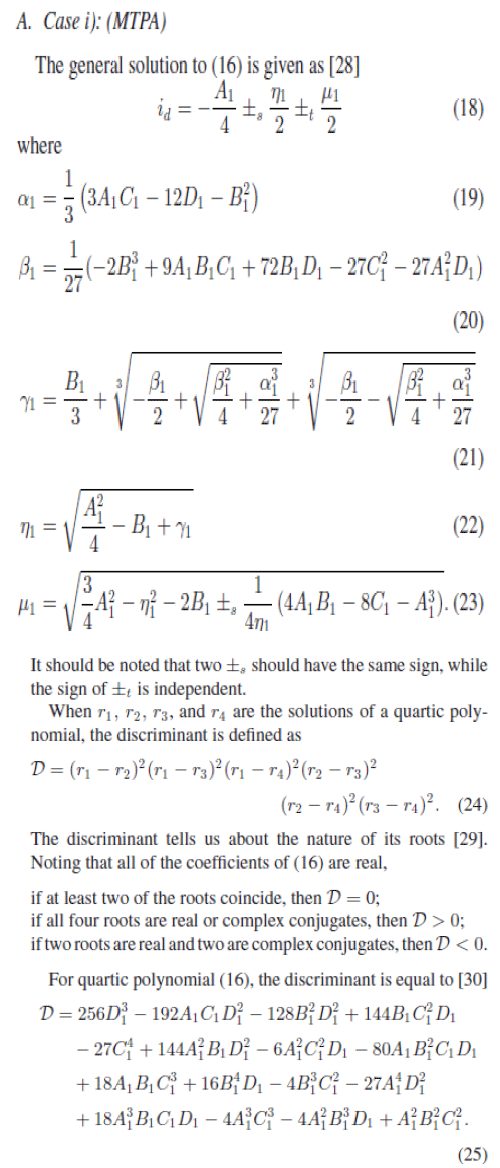 |
CONCLUSION FROM MTPA
|
| The current minimizing solution is found on the intersection with the MTPA or a voltage limit, depending on the speed and torque. Thus, before calculating the solution, it is necessary to classify the cases. A method suggested here is to find a solution candidate from Case ii), and check whether it is the (sub) optimal solution or not. Specifically, for a given T0 , determine the intersection with the voltage limit. Then, find the location of the MTPA solution. If the MTPA solution is within the voltage limit, we need to use the MTPA solution. Otherwise, the pre calculated solution (Case ii)) is determined to be the desired one. Because testing is conducted before finding the MTPA solution, unnecessary calculation effort can be avoided. This a priori determining method is based on the local geometric analysis at the intersection N(idβ, iqβ ). |
CONCLUDING REMARKS
|
| The current minimizing torque control method was considered for an IPMSM. In producing a desired torque, the current minimizing solution was sought. If the voltage limit was not active, it was possible to use the MTPA solution. Otherwise, it was necessary to use the intersection value between the voltage limit and torque curves. In both cases, quartic polynomials were induced, and Ferrari’s method was used to obtain general solutions for all of the quartic polynomials. |
| |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
| |
 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
Figure 8 |
|
| |
References
|
- S.Morimoto, M. Sanada, andY. Takeda, “Wide-speed operation of interior permanent magnet synchronous motors with high-performance current regulator,” IEEE Trans. Ind. Appl., vol. 30, no. 4, pp. 920–926, Jul./Aug. 1994.
- S. Morimoto, M. Sanada, and Y. Takeda, “Effects and compensation of magnetic saturation in flux-weakening controlled permanent magnet synchronous motor drives,” IEEE Trans. Ind. Appl., vol. 30, no. 6, pp. 1632– 1637, Nov./Dec. 1994.
- G. H. Kang et al., “Improved parameter modeling of interior permanent magnet synchronous motor based on finite element analysis,” IEEE Trans. Magn., vol. 36, no. 4, pp. 1867–1870, Jul. 2000
- B. Stumberger et al., “Evaluation of saturation and crossmagnetization effects in interior permanent-magnet synchronous motor,” IEEE Trans. Ind. Appl., vol. 39, no. 5, pp. 1264–1271, Sep. 2003.
- K. J. Meessen et al., “Inductance calculations of permanent-magnet synchronous machines including flux change and self- and crosssaturations,” IEEE Trans. Magn., vol. 44, no. 10, pp. 2324–2331, Oct. 2008.
- R. Nalepa and T. Orlowska-Kowalska, “Optimum trajectory control of the current vector of a nonsalient-pole PMSM in the field-weakening region,” IEEE Trans. Ind. Elec., vol. 59, no. 7, pp. 2867–2876, Jul. 2012.
- G. Kang et al., “A MTPA control scheme for an IPM synchronous motor considering magnet flux variation caused by temperature,” in Proc. IEEE APEC, Feb. 2004, pp. 1617–1621.
- R.Monajemy and R. Krishnan, “Implementation strategies for concurrent fluxweakening and torque control of thePMsynchronous motor,” in Proc. IEEE Ind. Appl. Society, Oct. 1995, pp. 238–245.
- Y. Jeong et al., “Online minimum-copper-loss control of an interior permanent-magnet synchronous machine for automotive applications,” IEEE Trans. Ind. Appl., vol. 42, no. 5, pp. 1222–1229, Sep./Oct. 2006.
- J. Lee et al., “Loss-minimizing control of PMSM with the use of polynomial approximations,” IEEE Trans. Power Elec., vol. 24, no. 4, pp. 1071– 1082, Apr. 2009.
|