Accurate, robust and automatic image registration is critical task in many applications. To perform image registration/alignment, required steps are: Feature detection, Feature matching, derivation of transformation function based on corresponding features in images and reconstruction of images based on derived transformation function. Accuracy of registered image depends on accurate feature detection and matching. So these two intermediate steps are very important in many image applications: image registration, computer vision, image mosaic etc. This paper presents two different methods for scale and rotation invariant interest point/feature detector and descriptor: Scale Invariant Feature Transform (SIFT) and Speed Up Robust Features (SURF). It also presents a way to extract distinctive invariant features from images that can be used to perform reliable matching between different views of an object/scene.
Keywords |
| Feature detection, Feature matching, SIFT, SURF, NCC |
INTRODUCTION |
| Lowe (2004) presented SIFT for extracting distinctive invariant features from images that can be invariant to image
scale and rotation. Then it was widely used in image mosaic, recognition, retrieval and etc [3]. Bay and Tuytelaars
(2006) speeded up robust features and used integral images for image convolutions and Fast-Hessian detector. Their
experiments turned out that it was faster and it works well [4]. |
| Image matching task to finding correspondences between two images of the same scene/object is part of many
computer vision applications. Image registration, camera calibration and object recognize just few. This paper describes
distinctive features from images is divided into two main phases. First, “key points” are extracted from distinctive
locations from the images such as edges, blobs, corner etc. Key point detectors should be highly repeatable. Next,
neighbourhood regions are picked around every key point and distinctive feature descriptors are computed from each
region [1]. |
| For image matching, extraction features in images which can provide reliable matching between different viewpoints of
the same image. During process, Feature descriptors are extracted from sample images and stored. This descriptor has
to be distinctive and, at the same time, robust to noise, detection errors. Finally, the feature descriptors are matched
between different images. Feature descriptor matching can be based on distances such as Euclidean. |
| This paper discusses the overview of the methods in Section 2, in section 3 we can see the experimental results while
Section 4 tells the conclusions of the paper. |
OVERVIEW OF METHODS |
| SIFT ALGORITHM OVERVIEW |
| SIFT (Scale Invariant Feature Transform) algorithm proposed by Lowe in 2004 [6] to solve the image rotation, scaling,
and affine deformation, viewpoint change, noise, illumination changes, also has strong robustness. |
| The SIFT algorithm has four main steps: (1) Scale Space Extrema Detection, (2) Key point Localization, (3)
Orientation Assignment and (4) Description Generation. |
| The first stage is to identify location and scales of key points using scale space extrema in the DoG (Difference-of-
Gaussian) functions with different values of σ, the DoG function is convolved of image in scale space separated by a
constant factor k as in the following equation. |
| D(x, y,σ) = (G(x, y, kσ) – G(x, y,σ) × I(x, y) …. (1) |
| Where, G is the Gaussian function and I is the image. |
| Now the Gaussian images are subtracted to produce a DoG, after that the Gaussian image subsample by factor 2 and
produce DoG for sampled image. A pixel compared of 3×3 neighborhood to detect the local maxima and minima of
D(x, y, σ). |
| In the key point localization step, key point candidates are localized and refined by eliminating the key points where
they rejected the low contrast points. In the orientation assignment step, the orientation of key point is obtained based
on local image gradient. In description generation stage is to compute the local image descriptor for each key point
based on image gradient magnitude and orientation at each image sample point in a region centered at key point [2]; these samples building 3D histogram of gradient location and orientation; with 4×4 array location grid and 8 orientation
bins in each sample. That is 128-element dimension of key point descriptor. |
| Construction Of SIFT Descriptor |
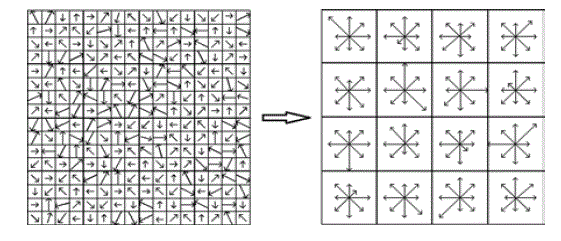
| Figure 1 illustrates the computation of the key point descriptor. First the image gradient magnitudes and orientations
are sampled around the key point location, using the scale of the key point to select the level of Gaussian blur for the
image [6]. In order to achieve orientation invariance, the coordinates of the descriptor, then the gradient orientations are
rotated relative to the key point orientation. Figure 1 illustrated with small arrows at each sample location on the left
side. |
| The key point descriptor is shown on the right side of Figure 1. It allows for significant shift in gradient positions by
creating orientation histograms over 4x4 sample regions. The figure shows 8 directions for each orientation histogram
[6], with the length of each arrow corresponding to the magnitude of that histogram entry. A gradient sample on the left
can shift up to 4 sample positions while still contributing to the same histogram on the right. So, 4×4 array location grid
and 8 orientation bins in each sample. That is 128-element dimension of key point descriptor. |
| SURF Algorithm Overview |
| SURF (Speed Up Robust Features) algorithm, is base on multi-scale space theory and the feature detector is base on
Hessian matrix. Since Hessian matrix has good performance and accuracy. In image I, x = (x, y) is the given point, the
Hessian matrix H(x, σ) in x at scale σ, it can be define as |
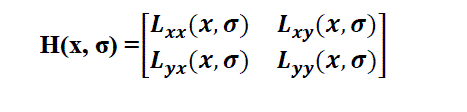 (2) (2) |
Where Lxx (x, σ) is the convolution result of the second order derivative of Gaussian filter 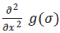 with the image I
in point x, and similarly for Lxy (x, σ) and Lyy (x, σ). with the image I
in point x, and similarly for Lxy (x, σ) and Lyy (x, σ). |
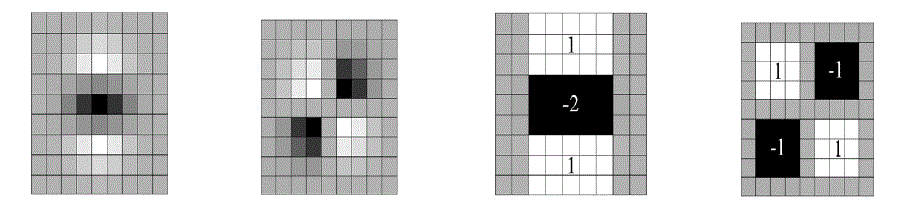
| SURF creates a “stack” without 2:1 down sampling for higher levels in the pyramid resulting in images of the same
resolution. Due to the use of integral images, SURF filters the stack using a box filter approximation of second-order
Gaussian partial derivatives [3]. Since integral images allow the computation of rectangular box filters in near constant
time. In Figure 2 Show the Gaussian second orders partial derivatives in y-direction and xy-direction. |
| In descriptors, SIFT is good performance compare to other descriptors. The proposed SURF descriptor is based on
similar properties. The first step consists of fixing a reproducible orientation based on information from a circular
region around the interest point. And second construct a square region aligned to the selected orientation, and extract
the SURF descriptor from it. In order to be invariant to rotation, it calculate the Haar-wavelet responses in x and y
direction shown in figure 3. |
EXPERIMENTAL RESULTS |
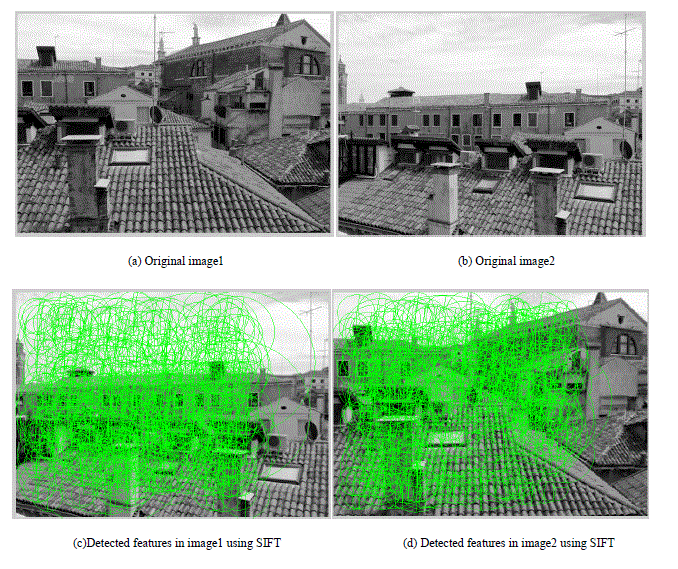
| To verify the effectiveness of the algorithm two images are taken as the experimental data as shown in figure 1 (a)
image1: 640×478, 153 KB and (b) image2: 640×478, 127 KB. The experiments are performed on Intel Core i-3 3210,
2.3 GHz processor and 4 GB RAM with windows 7 as an operating system. Features are detected in both images using
SIFT and SURF algorithm. Figure 4 (c) and (d) shows the detected features using SIFT in image1 and image2
respectively. It is observed that 892 features are detected in image1 and 934 features are detected in image2. |
| Figure 4 (f) and (g) shows the detected features using SURF algorithm from the original image1 & image2
respectively. It is observed that 281 features are detected in image1 and 245 features in image2. |
 |
 |
| The features matching is shown in Figure 4(e) are 41 and Figure 4(h) shows 28 matched points. Normalised Cross
Correlation technique is used here for feature matching. The experimental results are summarised in Table 1. |
CONCLUSIONS |
| This paper has evaluated two feature detection methods for image registration. Based on the experimental results, it is
found that the SIFT has detected more number of features compared to SURF but it is suffered with speed. The SURF
is fast and has good performance as the same as SIFT. Our future scope is to make these algorithms work for the video
registration. |
ACKNOWLEDGMENT |
| Authors of this paper are thankful, to David Lowe for extending help in developing SIFT code and helpful advice on
this topic, also to Bay and Tuytelaars for providing help in generating SURF code and helpful advice on this topic. |
Tables at a glance |
 |
| Table 1 |
|
Figures at a glance |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
References |
- Nabeel Younus Khan, Brendan McCane, and Geoff Wyvill, “SIFT and SURF Performance Evaluation against Various Image Deformations on Benchmark Dataset”, International Conference on Digital Image Computing: Techniques and Applications, pp.501-506, 2011.
- ViniVidyadharan, and SubuSurendran, “Automatic Image Registration using SIFT-NCC”, Special Issue of International Journal of Computer Applications (0975 – 8887) , pp.29-32, June 2012.
- Luo Juan, and Oubong Gwun, “A Comparison of SIFT, PCA-SIFT and SURF”, International Journal of Image Processing (IJIP), Vol. 3, Issue 4, pp. 143-152.
- Herbert Bay, Tinne Tuytelaars, and Luc Van Gool, “SURF: Speeded Up Robust Features”, pp. 1-14.
- Seok-Wun Ha, Yong-Ho Moon, “Multiple Object Tracking Using SIFT Features and Location Matching” ,International Journal of Smart Home Vol. 5, No. 4,pp. 17-26, October 2011.
- D. Lowe. “Distinctive Image Features from Scale-Invariant Keypoints”, Accepted for publication in the International Journal of Computer Vision, pp. 1-28, 2004.
- Hongbo Li, Ming Qi And Yu Wu, “A Real-Time Registration Method Of Augmented Reality Based On Surf And Optical Flow”, Journal Of Theoretical And Applied Information Technology, Vol. 42, No.2, pp. 281-286, August 2012.
|