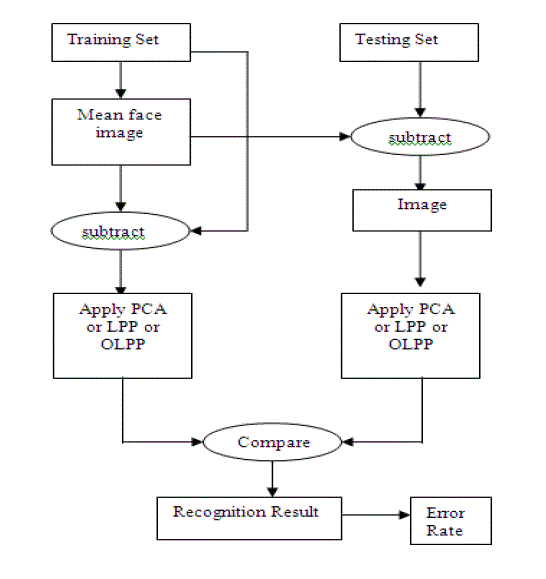
Facial analysis and recognition is one of the most popular information processing tasks. Face recognition requires some form of dimensionality reduction in the face dataset. There are numerous face representation and recognition techniques which vary in their complexity and efficiency. In this study, we have done a comparative analysis of Eigenfaces based on Principal Component Analysis (PCA), Laplacianfaces based on Locality Preserving Projection (LPP) and Orthogonal Laplacianfaces based on Orthogonal LPP (OLPP), on a standard face database- YALE. PCA is an eigenvector method which aims to preserve the global Euclidean structure of the face space. Its goal is to find a set of mutually orthogonal basis functions that capture the directions of maximum variance in the data. LPP method finds an embedding that preserves local information and obtains a face space that explicitly considers the manifold structure. LPP algorithm aims at finding a linear approximation to the eigen functions of the Laplace Beltrami operator on the face manifold which reflects the intrinsic face manifold structure. OLPP algorithm is based on the LPP algorithm. However, LPP is non-orthogonal and this makes it difficult to reconstruct the data. The OLPP method produces orthogonal basis functions and can have more locality preserving power than LPP. Nearest neighbor classification using OLPP are used to obtain the error rate.
Keywords |
| Face Recognition, Principal Component Analysis, Locality Preserving Projections, Orthogonal locality
preserving projection, Face Manifold, Subspace Learning |
INTRODUCTION |
| Face recognitions an emerging concept in the field of research in Computer science and technology[1]. There are
numerous face recognition techniques developed in past few decades. The face recognition techniques can be grouped
into: appearance based technique, feature based technique, model based technique [1][6]. One of the most successful
and well studied techniques is the appearance based methods[6]. In this method, we consider an image of size m by n
pixels as a vector drawn in a mn dimensional space. However, this ‘mn’ dimensional space is too large to allow
efficient and quick computation and also results in a training set that is too big to work on. Hence, some form of
dimensionality reduction is required to work with such methods [3][4][5][6]. The classical but popular form of linear
technique is method of Principal Component Analysis (PCA) [6][13][17]which is an eigenvector method designed to
model linear variations in a high-dimensional data. |
| PCA approach was developed by Turk and Pentland [6] to describe face images in term of set of basic functions or
“Eigenfaces”. PCA performs dimensionality reduction by projecting the high dimensional data onto a lower
dimension[16] subspace that is formed by taking “principal” eigenvectors of the covariance matrix of data. PCA
effectively view the overall global or Euclidean structure of the face images and do not take into account the nonlinear
structure of the face manifold hidden in image space. The Laplacianface method [4] is proposed by Xiao fei He, to
model the local manifold structure. The Laplacianfaces are the linear approximations to the eigen functions of the
Laplace Beltrami operator on the face manifold[16]. A face subspace is obtained by Locality Preserving Projections
(LPP) [4][9][3]. Each face image in the image space is mapped to a low dimensional face subspace, which is
characterized by a set of feature images, called Laplacianfaces. The face subspace preserves local structure, seems to
have more discriminating power than the PCA approach for classification purpose However, the basic functions
obtained by the Laplacianface method are non-orthogonal. This makes it difficult to reconstruct the data. |
| An appearance based approach called orthogonal laplacianfaces proposed by Deng caiet al.[3]. O-Laplacianface is
fundamentally based on the Laplacianface method. It builds an adjacency graph which can best reflect the geometry of
the face manifold and the class relationship between the sample points. The projections are then obtained by preserving
such a graph structure. It shares the same locality preserving character as Laplacianface, but it also requires the basis
functions to be orthogonal. Orthogonal basis functions preserve the metric structure of the face space. |
| In fact, if we use all the vectors obtained by O-Laplacianface, the projection subspace is a rotation map which does not
distort the metric structure. As it is given that the locality preserving power is directly related to the discriminating
power [11], theO-Laplacianface is expected to have more discriminating power than Laplacianface. In this study, we
have done a comparative analysis of Eigenfaces based on Principal Component Analysis (PCA), Laplacianfaces based
on Locality Preserving Projection (LPP) and Orthogonal Laplacianfaces based on Orthogonal LPP (OLPP), on a
standard face database- YALE. The general flow diagram of above approaches is shown below: |
LITERATURE SURVEY |
| In LPP, the face images are mapped into a face subspace for analysis[4][8]. Different from Principal Component
Analysis (PCA) which effectively see only the Euclidean structure of face space [6][9].LPP finds an embedding that
preserve local information, and obtains a face subspace that best detects the essential face manifold structure[4]. |
| It was the first devoted work on face representation and recognition which explicitly considers the manifold structure.
The manifold structure is approximated by the adjacency graph computed from the data points. Using the notion of the
Laplacian of the graph, a transformation matrix was computed which maps the face images into a face subspace. |
| OLPP is based on the LPP algorithm, which aims at finding a linear approximation to the eigenfunctions of the Laplace
Beltrami operator on the face manifold[3]. However, LPP is non- orthogonal and this makes it difficult to reconstruct
the data.The OLPP method produces basis functions and can have more locality preserving power than LPP. Since the locality preserving power is potentially related to the discriminating power, the OLPP is expected to have more
discriminating power too. |
EIGENFACES APPROACH |
| Proposed in 1991 by Turk and Pentland [6], this was the first genuinely successful system for automatic recognition of
human faces. It was a breakaway from contemporary research trend on face recognition which focused on detecting
individual features such as eyes, nose, mouth, and head outline, and defining a face model based on position and size of
these features, as well as geometrical relationship between them. Despite being economical representations of a face,
these methods are quite sensitive to the feature extraction and measurement process [18]. Lack of existing techniques for
effective extraction and measurement of facial features presents a drawback for such methods [19]. |
| The task of facial recognition is discriminating input signals (image data) into several classes (persons). The input
signals are highly noisy (e.g. the noise is caused by differing lighting conditions, pose etc.), yet the input images are not
completely random and in spite of their differences there are patterns which occur in any input signal. Such patterns,
which can be observed in all signals could be - in the domain of facial recognition - the presence of some objects (eyes,
nose, mouth) in any face as well as relative distances between these objects. These characteristic features are called
eigenfaces in the facial recognition field (or principal components generally). They can be extracted out of original
image data by means of a mathematical tool known as PCA. These components span a subspace within the image
space where each different face in the training set has a unique position. The Eigenfaces emphasize significant
discriminatory “features” that causes large variations between the faces used for training, which subsequently allows
them to be differentiated. It should be noted that these features may not necessarily correspond to facial features
mentioned earlier. Recognition is then performed by projecting the test image into the subspace spanned by the
Eigenfaces and classified based on the distance of the projection from positions of known faces. |
| By means of PCA one can transform each original image of the training set into a corresponding eigenface. An
important feature of PCA is that one can reconstruct any original image from the training set by combining the
eigenfaces. Remember that eigenfaces are nothing less than characteristic features of the faces. Therefore one could say
that the original face image can be reconstructed from eigenfaces if one adds up all the eigenfaces (features) in the right
proportion. |
Principal Component Analysis |
| Given an s-dimensional vector representation of each face in a training set of M images, PCA [6][22][9] tends to find a
t-dimensional subspace whose basis vectors correspond to the maximum variance direction in the original image space.
This new subspace is normally lower dimensional (t <<s). New basis vectors define a subspace of face images called
face space. All images of known faces are projected onto the face space to find a set of weights that describes the
contribution of each vector. To identify an unknown image, that image is projected onto the face space to obtain its set
of weights. By comparing a set of weights for the unknown face to sets of weights of known faces, the face can be
identified. If the image elements are considered as random variables, the PCA basis vectors are defined as eigen vectors
of the scatter matrix ST defined as: |
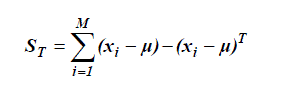 |
| where μ is the mean of all images in the training set (the mean face) and xi is the i-th image with its columns
concatenated in a vector. The projection matrix WPCA is composed of teigenvectors corresponding to t largest
eigenvalues, thus creating a t-dimensional face space. We implemented PCA procedure as described in [6]. |
LAPLACIANFACES APPROACH |
| In this section, we describe LPP [8][4], an algorithm for learning a locality preserving subspace. Each face image in the
image space is mapped to a low dimensional face subspace which is obtained by LPP, which is characterized by a set of
feature images, called Laplacianfaces. It builds a graph incorporating neighborhood information of the data set. Using
the notion of the Laplacian of the graph[11], we then compute a transformation matrix which maps the data points to a
subspace. This linear transformation optimally preserves local neighborhood information in a certain sense. The
representation map generated by the algorithm may be viewed as a linear discrete approximation to a continuous map
that naturally arises from the geometry of the manifold [1][2][12]. The LPP algorithm is interesting from a number of
perspectives [8]. 1) The maps are designed to minimize a different objective criterion from the classical linear
techniques. 2) The locality preserving quality of LPP is likely to be of particular use in information retrieval
applications. If one wishes to retrieve audio, video, text documents under a vector space model, then one will ultimately
need to do a nearest neighbor search in the low dimensional space. Since LPP is designed for preserving local structure,
it is likely that a nearest neighbor search in the low dimensional space will yield similar results to that in the high
dimensional space. This makes for an indexing scheme that would allow quick retrieval. 3) LPP is linear. This makes it
fast and suitable for practical application. While a number of non linear techniques have properties (1) and (2) above, we
know of no other linear projective technique that has such a property. 4) LPP is defined everywhere. Recall that
nonlinear dimensionality reduction[7] techniques like ISOMAP[6], LLE[5], Laplacian eigenmaps[2] are defined only on
the training data points and it is unclear how to evaluate the map for new test points. In contrast, the Locality Preserving
Projection may be simply applied to any new data point to locate it in the reduced representation space. |
| As a result of all these features, we expect the LPP based techniques[4][3] to be a natural alternative to PCA based
techniques in exploratory data analysis, information retrieval, and pattern classification applications. The complete
derivation and theoretical justifications of LPP can be traced back to [8]. LPP seeks to preserve the intrinsic geometry of
the data and local structure. Given a set of face images {x1 , x2 .........., xn } ⊂
Rm , let X= {x , x .........., x } 1 2 n . Let S be a
similarity matrix defined on the data points. Laplacianface can be obtained by solving the following minimization
problem |
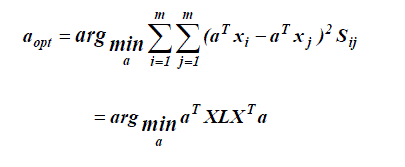 |
| with constraint aT XDX T a = 1where L=D-S is the graph Laplacian[4] and ii ii j ij D ij = ΣjSij .Dii measures the local
density around xi |
| A. Calculation of Laplacianfaces with LPP |
| The algorithmic procedure of LPP is given below: |
| 1) PCA projection. |
| We project the image set into the PCA subspace by throwing away the smallest principal components. x to denote
the images in the PCA subspace in the following steps. We denote by WPCA the transformation matrix of PCA. |
| 2) Constructing the nearest-neighbor graph. |
| Let G denote a graph with n nodes. The ith node corresponds to the face image xi. We put an edge between nodes i
and j if xi and xi are “close,” i.e., xi is among k nearest neighbors of xi, or xi is among k nearest neighbors of xj. The
constructed nearest neighbor graph is an approximation of the local manifold structure. |
| 3) Choosing the weights. |
| If node i and j are connected, put |
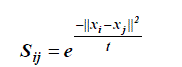 |
| where t is a suitable constant. Otherwise, put Sij = 0.The weight matrix S of graph G models the face manifold structure
by preserving local structure. |
| 4) Eigenmap |
| Compute the eigenvectors and eigenvalues for the generalized eigenvector problem |
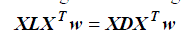 (1) (1) |
| where D is a diagonal matrix whose entries are column (or row, since S is symmetric) sums of S, Dii = ΣjSji. L =D - S is
the Laplacian matrix. The ith row of matrix X is xi. |
| Let w0, w1, …,wk-1be the solutions of equation (1), ordered according to their Eigenvalues,0≤λ0≤λ1…≤λk-1.These
Eigenvalues are equal to or greater than zero because the matrices XLXT and XDXT are both symmetric and positive
semi definite. Thus, the embedding is as follows: |
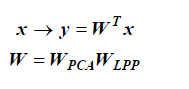 |
| where, |
| WLPP=[w0;w1; . . . ;wk-1 ] ; |
| WPCA=Transformation matrix of PCA; |
| W=Transformation matrix of Laplacianface. |
| This linear mapping best preserves the manifold’s estimated intrinsic geometry in a linear sense. The column vectors of
W are the so-called Laplacianfaces. XDXT is non-singular after some pre-processing steps on X in Laplacianface, thus,
the basic functions of Laplacianface can also be regarded as the eigenvectors of the matrix (XDXT)-1 XLXT associated
with the smallest eigenvalues. Since (XDXT)-1 XLXT is not symmetric in general, the basic functions of Laplacianface
are non-orthogonal. |
ORTHOGONAL LAPLACIANFACES APPROACH |
| Orthogonal Laplacianfaces is based on Orthogonal LPP. OLPP is a novel subspace learning algorithm presented by Den
cai et al.[3].This algorithm is built on the base of the LPP method[5] and primarily devised to solve the problem of face
recognition. Actually, OLPP is an effective dimensionality reduction method falling into category of manifold
learning[15].In appearance-based face analysis one is often confronted with the fact that the dimension ofthe face image
vector (m) is much larger than the number of face images (n). Thus, the m × m matrix XDXT is singular. To overcome
this problem, we can first apply PCA to project the facesinto a subspace without losing any information and the matrix
XDXT becomes non-singular. |
| The algorithmic procedure of OLPP is stated below |
| 1) PCA projection |
| Projecting the high dimensionality points xi into the PCA subspace by throwing away the components
corresponding to zero eigenvalue. The transformation matrix of PCA is WPCA . |
| 2) Constructing the nearest-neighbor graph |
| Let G denote a graph with n nodes. The ith node corresponds to the face image xi. We put an edge between nodes i
and j if xi and xj
are “close,” i.e., xj is among k nearest neighbors of xi, or xi is among k nearest neighbors of xj. The
constructed nearest neighbor graph is an approximation of the local manifold structure. Note that here we do not use
the neighborhood to construct the graph. This is simply because it is often difficult to choose the optimal “in the
real-world applications, while k nearest-neighbor graph can be constructed more stably. The disadvantage is that the k nearest-neighbor search will increase the computational complexity of algorithm. When the computational
complexity is a major concern, one can switch to the ε -neighborhood. |
| 3) Choosing the weights |
| If node i and j are connected, put |
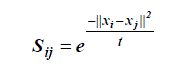 |
| Where t is a suitable constant. Otherwise, put Sij = 0.The weight matrix S of graph G models the face manifold structure
by preserving local structure. |
| 4) Computing the Orthogonal Basis Function |
| Let w1 ,w2 ,.......,wk be orthogonal basis vectors, defining |
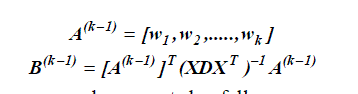 |
| The orthogonal basis vectors w1 ,w2 ,.......,wk can be computed as follow. |
| • Compute w1 as the eigenvector of (XDXT)-1 XLXT associated with the smallest eigenvalue. |
| • Compute wk as the eigenvector of |
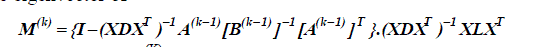 |
| associated with the smallest eigenvalue of M(K). |
| 5) OLPP Embedding |
| Let WOLPP = [w1,w2,.........,wl ] , the embedding is as follows. |
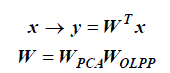 |
| Where y is a l -dimensional representation of the face image x, and W is the transformation matrix. |
| In this paper, utilizing the orthogonality of the base functions, we reduce the dimensionality of face space and then
reconstruct the data. |
EXPERIMENTAL RESULTS |
| A face image can be represented as a point in image space. However, due to the unwanted variations resulting from
changes in lighting, facial expression, and pose, the image space might not be an optimal space for visual representation.
We can display the eigenvectors as images. The recognition process has three steps. First, we calculate the face subspace
from the training samples; then the new face image to be identified is projected into d-dimensional subspace by using
our algorithm; finally, the new face image is identified by a nearest neighbor classifier[3][4]All recognition algorithms
and all image preprocessing[2] steps were implemented in MATLAB 7.8.0.347 |
Recognition Analysis |
| In this sub-section, we compare the three approaches for face representation, i.e., Eigenface, Laplacianface and OLaplacianface.
For each of them, the basis vectors can be thought of as the basis images and any other image is a linear
combination of these basis images. The Yale face database was constructed at the Yale Center for Computational
Vision and Control [20]. It contains 165 grayscale images of 15 individuals. The database contains 165 GIF images of
15 subjects There are 11 images per subject, one for each of the following facial expressions or configurations: centerlight,
w/glasses, happy, left-light, w/no glasses, normal, right-light, sad, sleepy, surprised, and wink. Images are of GIF format and size is 320x240.By varying images from 1 to 10 per subject, the training set has been created. The rest was
taken for testing. The testing samples were then projected into the low-dimensional Representation. Recognition was
performed using a nearest-neighborclassifier. |
| In general, the performance of the Eigenfaces method, the Laplacianfaces method and O-Laplacianfaces method varies
with the number of images used for training. We show the best results obtained by Eigenfaces, Laplacianfaces and OLaplacainfaces.
The performance comparison between Laplacianfaces, PCA and O-Laplacianfaces on 2,4,5 training
images per subject with different value of subDim given in bracket are shown in Table 1. It is found that the OLaplacianfaces
method significantly outperforms Eigenfaces method and Laplacianfacs method. Note: subDim here
indicates number of principal components chosen for an image. Graph has been plotted for the 2,4,5 training images per
subject with varying subDim shown in Fig. 2.Table 1 shows the best results obtain by above three method with different
training images for particular subDim. Table 2 presents percentage error rate reduction for LPP and OLPP on 2,4,5
training images per subject. |
CONCLUSION |
| A comparative study of the error rate between PCA approach, Laplacianfaces approach and O-Laplacianfaces has
been done. We have found that O-Laplacianfaces consistently perform better than Eigenfaces and Laplacianfaces for 2,
4 and 5 training images per subject. The algorithms applied takes advantage of more training samples, which is
important to the real world face recognition systems. Comparing to the Eigenfaces method and Laplacianfaces method,
the O-Laplacianfaces method encodes more discriminating information by preserving local structure. By discovering the
face manifold structure, Laplacianfaces can identify the person with different expressions, poses and lighting conditions.
Experimental results show the effectiveness of the O-Laplacianface method, Laplacianfaces method and Eigenfaces
method. Thus we can conclude that local manifold learning techniques prove to be better than the traditional global
manifold based techniques, which consider only the Euclidean structure and do not take into account the local features.
Also, considering the Fig 2 we can conclude which method out of the three is better on what range of sub dimensions
taken. |
| |
Tables at a glance |
 |
 |
| Table 1 |
Table 2 |
|
| |
Figures at a glance |
 |
 |
| Figure 1 |
Figure 2 |
|
| |
References |
- Li S.Z. and Jain A.K.. Handbook of Face recognition, Springer Science+Business Media, Inc.,ch-1,2,3,7,and 9,pp.1-51,141-154,193-210,2005
- Gonzalez R.C. and Woods R.E. Digital Image Processing, Prentice hall, Ch-1and 2,pp. 1-70,second edition.
- Cai D., He X. and Zhang J.H.H, “Orthogonal Laplacianfaces for Face Recognition”IEEE Transactions on Image Processing, VOL. 15, NO. 11,pp.3608-3614, NOVEMBER 2006.
- He X., Yan S., Hu Y., Niyogi P. and Zhang H., “Face Recognition Using Laplacianfaces”, IEEE Transactions on Pattern Analysis and MachineIntelligence, Vol.27 No.3, pp.328-340, March 2005.
- Belhumeur P.N., Hespanha J.P., and Kriegman D.J., “Eigenfaces vs. Fisherfaces: Recognition Using Class Specific Linear Projection”, IEEETransactions On Pattern Analysis and Machine Intelligence, Vol. 19, No. 7, pp.711-720, July 1997.
- Turk M. and Pentland A., “Eigenfaces for Recognition,” J. Cognitive Neuroscience, vol. 3, no. 1,pp. 585-591, 1991.
- Roweis S.T. and Saul L.K., “Nonlinear Dimensionality Reduction by Locally Linear Embedding”, Science, vol 290, 22 December 2000.
- He X. and Niyogi P., “Locality Preserving Projections”, Advances in Neural Information Processing Systems, Vancouver, Canada, 2003.
- Vishwakarma V.P., Pandey S. and Gupta M.N., Face Recognition”, IACSIT International Journal of Engineering and Technology Vol. 2, No.1,February, 2010 ISSN: 1793-8236,pp 117-123. “Fuzzy based Pixel wise Information Extraction for
- Klir G.J. and Yuan B., “Fuzzy Sets and Fuzzy Logic: Theory and Application,” Prentice Hall, New Jersey,1995.
- BelkinM.andNiyogi P., “LaplacianEigenmaps and Spectral Techniques for Embedding and Clustering”, Advances in Neural Information Processing System 15, Vancouver, British Columbia, Canada, 2001.
- Hu Y.C.C and Turk M., “Manifold of Facial Expression”, Proc. IEEE International Workshop on Analysis and Modeling of Faces andGestures, Nice, France, Oct 2003.
- Martinez A.M. and Kak A.C., “PCA versus LDA”, IEEE Trans. on Pattern Analysis and Machine Intelligence, 23(2):228-233, 2001
- Duchene J. and Leclercq S. An optimal transformation for discriminant and principal component analysis. IEEE Trans. on PAMI, 10(6):978–983, 1988.
- Seung H.S. and Lee D.D , “The Manifold Ways of Perception”, Science, vol 290, 22 December 2000.
- Sirovitch L. and Kirby M., “Low-Dimensional Procedure for the Characterization of Human Faces,” J. Optical Soc. of Am. A, vol. 2, pp. 519-524, 1987.
- Chellappa W.Z.R., Krishnaswamy A., "Discriminant Analysis of Principal Components for Face Recognition", Proc. of the 3rd IEEEInternational Conference on Automatic Face and Gesture Recognition, 14-16 April 1998, Nara, Japan, pp. 336-341
- Georghiades, A.S.,Belhumeur P.N., and Kriegman D.J., From Few to Many: Illumination Cone Models for Face Recognition under VariableLighting and Pose. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001. 23(6): p. 643-660.
- Cox, I., Ghosn J., and YianilosP.. Feature-based Face Recognition Using Mixture Distance. inProceedings IEEE Conference on ComputerVision and Pattern Recognition. 1996.
- Yale Univ. Face Database, http://cvc.yale.edu/projects/yalefaces/yalefaces.html, 2002
|