A Fast Fault Classification Technique for
Power Systems

H. Nouri; C. Wang

A Fast Fault Classification Technique for Power Systems

H. Nouri and C. Wang
Power Systems, Electronics and Control Research Laboratory, UWE Bristol, UK

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper proposes a fast fault classification technique using three phase current signals for power systems. Digital Fourier Transform, the ‘Least Square’ method or the Kalman Filtering technique are used to extract fundamental frequency components of three phase fault currents. Fast fault classification can be achieved using the fault probability of three phases. Results from simulation work on EMTP have validated the proposed fault classification technique. The response time of the fault classification technique using the ‘Least Squares’ method is 1.875ms (3 samples) for single-phase-to-earth fault, two-phase-to-earth fault, two-phase-fault and three-phase fault.

Keywords

Fault classification, Fourier transforms, least squares method, Kalman filter

INTRODUCTION

Fault classification is an important function for power systems protection and fault locators. A modular methodology [1] is used for fast fault classification. Girgis [2-3] uses an adaptive Kalman filters technique and a probabilistic technique for fault classification. One Kalman filter assumes the features of the faulted phase while the other has features of an un-faulted phase. The condition of the phase, faulted or non-faulted, is then decided from the computed probabilities. Barros and Drake [4] implement 8-bit microprocessors for fault classification based on Kalman filters. The response time is less than 20 ms for all possible types of ground fault. Artificial intelligent techniques are also used for fault classification, such as the neuro-fuzzy approach [5], probabilistic neural networks [6], neural networks [7] and combined unsupervised/supervised neural networks [8]. Zhao [9] applies a wavelet transform based scheme for fault classification.

This paper proposes a fast fault classification technique for fault locators. Digital Fourier Transform (DFT), or the Least Squares Method (LSM), or Kalman Filtering Technique (KFT) is used to extract fundamental frequency components of three phase currents. Fault classification of three phases can be made by using of the fault probability method. Results from EMTP/ATP simulations are presented. The fault classification technique using the ‘Least Squares’ method can operate correctly within 3 samples (1.875ms) for single line-to-ground (SLG) faults, double lineto- ground (2LG) faults, line-to-line (LL) faults and three-phase (3φ) faults.

FAULT CLASSIFICATION

Fault classification is determined by fault probabilities of three phases. Fault probability of phases depends upon the amplitude of the fundamental components of three phase currents, Ia(t), Ib(t) and Ic(t), which are calculated using fundamental frequency component extracting techniques, such as DFT, LSM or KFT.

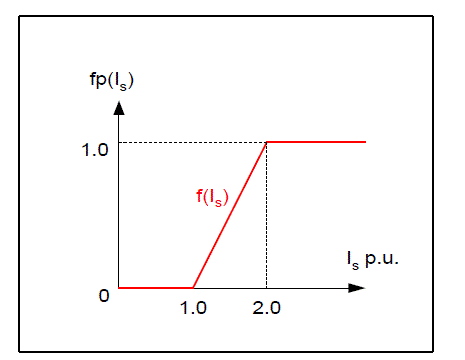
(a) Fault probability function

There is a relation between fault probability and amplitude of fundamental frequency current Is (S = A, B, C). When Isis a load current, its fault probability is low (close to 0) and if Is is a fault current, the fault probability will be high (close to 1.0 i.e.100%). So, it is reasonable to assume that the fault probabilities are as follows (there are also other similar functions):

fp(S) =f(Is)=0 (Is<1.0 p.u.) (S = A, B, C)

=f(Is)=(Is-1.0) (1.0<Is<2.0 p.u.)

=f(Is)=1.0 (Is>2.0 p.u.)

Per unit based on maximum load current is used. The probability function is shown in fig 1.

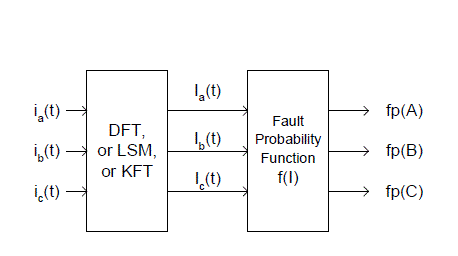
(b) Functional block diagram

A block diagram of fault classification is shown in fig 2. The input signals are three phase current ia(t), ib(t) and ic(t). Amplitudes of fundamental frequency current Ia(t), Ib(t) and Ic(t) are calculated using mathematical algorithm DFT, or LSM, or KFT. Fault probability fp(A), fp(B) and fp(C) can be obtained from fault probability function f(I).

SIMULATION RESULTS

To validate the proposed fault classification technique, a two-source system [4] is used. Parameters of the two-source system are Z_>SA=0+j21.5 ohms; Z_>0SA=0+j24.4 ohms; Z_>SB=0+j25.6 ohms; Z_>0SB=0+j27.8 ohms. Line impedance Z_>L=3.4+j53.4 ohms and Z_>0L=57.0+j241 ohms. The source voltage is E_A=225.17+j0 kV and E_B=169.86-j169.86 kV. A sample rate of 32 samples per cycle (Δt=0.625 ms) is used.

All simple fault types, such as single-phase-to-earth faults (LG), two-phase-to-earth faults (2LG), two-phase-short circuit faults (LL) andthree-phase-short-circuit faults (3φ are taken into account. Fault resistance with zero and 10 ohms are considered at faultpoint. The simulation results are listed in table I and II. In these tables, the minimum sample is counted from faultoccurrence (sample=0) to the sample at which fault probability of the faulty phase hasreached100%, i.e. values with1.0.

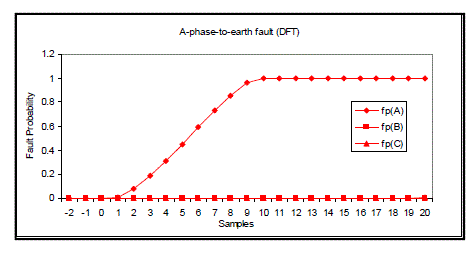
(a) Digital Fourier Transform (DFT)

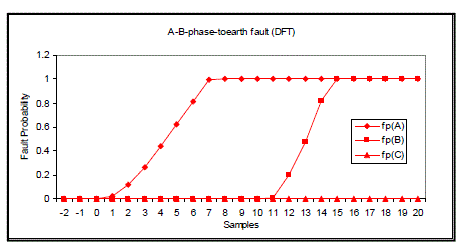
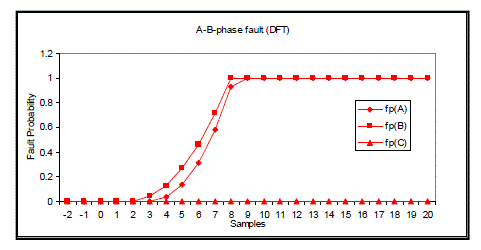
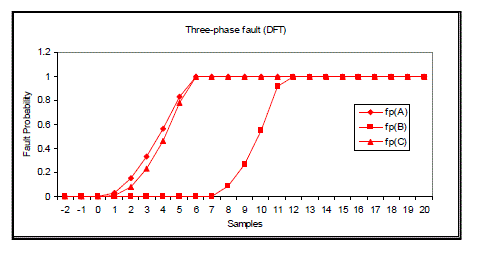
For A-phase-to-earth fault, the fault probability of A phase reaches 1.0 after 10 samples when the fault occurs. The result is shown in fig 4. It is the same for B-phase-to-earth fault (10 samples) and C-phase-to-earth fault (9 samples).Therefore there are 10 samples in table I. In a similar way, fig 5 shows fault classification results for A Bphase- to earth fault, fig 6 for A-B-phase short circuit fault and fig 7 for three-phase fault.

(b) Least Squares Method (LSM)

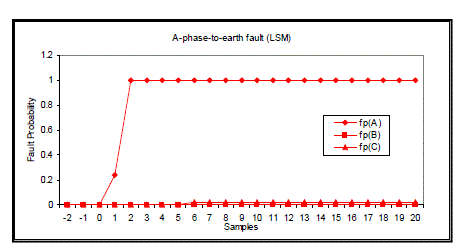
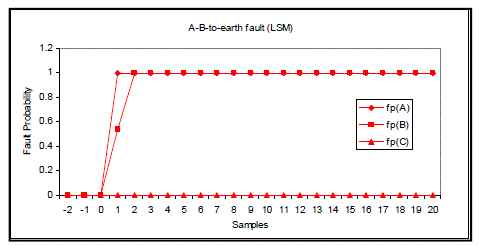
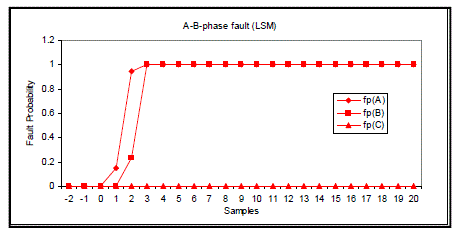
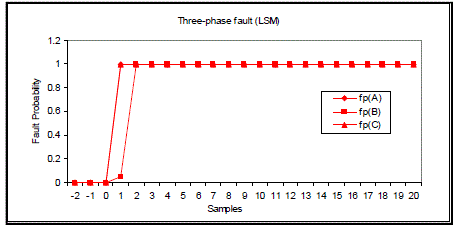
Figs. 8 to 11 show fault classification results using LSM. It is easy to find that 2 samples are needed for correctly classifying A-phase-to-earth fault, 2 samples for A-B-phase-to-earth fault, 3 samples for A-B-phase short circuit and 2 samples for three-phase-short circuit fault.

(c) Kalman Filtering Technique (KFT)

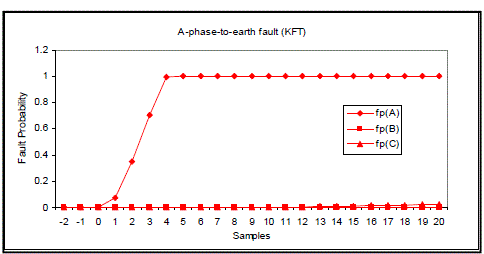
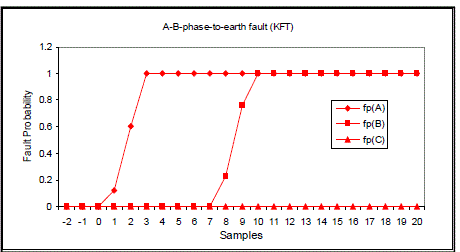
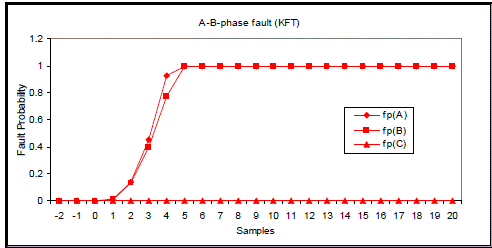
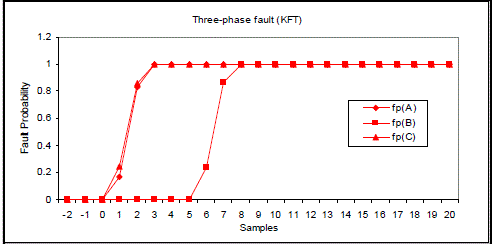
Figs 12 to 15 show fault classification results using KFT. It can be seen that 5 samples are needed for correctly classifying A-phase-to-earth fault, 10 samples for A-B-phase-to-earth fault, 5 samples for A-B-phase short circuit and 8 samples for three-phase-short circuit fault.

COMPARISON

(1) Among the three methods, performance of simulation results using LSM with 6 samples is the most effective. Fault classification using LSM can give correct fault phase detection within 3 samples (1.875ms) for all four types of simple fault. On the other hand, KFT needs 10 samples (6.25 ms) and DFT needs 15 samples (9.375 ms) to represent correct fault types.

(2) There are no significant changes for 0-10 ohms fault resistance at fault point. The reason may be that the fault resistance affects the amplitude of fundamental frequency fault current, but the fault current is much more than the threshold value (2.0 p.u.) for a fault probability of 1.0.

CONCLUSION

This paper proposes a fast fault classification technique using current signals for fault locators in power systems. Digital Fourier Transform, the Least Square Method or the Kalman Filtering Technique are used to extract fundamental frequency components of three phase fault currents. Fault classification can be made using fault probability of the three phases. Results from simulation work on an EMTP are presented. The fault classification technique using the ‘least square’ method can operate correctly within 3 samples (1.875ms) for single line-to-ground faults, double line-to-ground faults, line-to-line faults and three-phase faults.

Tables at a glance


Table 1	Table 2

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4	Figure 5


Figure 6	Figure 7	Figure 8	Figure 9	Figure 10


Figure 11	Figure 12	Figure 13	Figure 14	Figure 15

References

Chowdhury F N and Aravena J L, A modular methodology for fast fault detection and classification in power systems, IEEE Transactions on Control Systems Technology, Vol. 6, No.5, pp.623-634, September 1998.

Girgis A A, et al, Application of adaptive Kalman filtering in fault classification, distance protection and fault location using microprocessor, IEEE transactions on Power Systems, vol. 3, pp.301-309, 1988.

Girgis A A and Brown R G, Adaptive Kalman filtering in computer relaying: Fault classification using voltage model, IEEE Transactions on PAS, Vol. PAS-104, No.5, pp.1168-1177, May 1985.

Barros J and Drake J M, Real time fault detection and classification in power systems using microprocessors, IEE Proceeding on Generation, Transmission and Distribution, Vol.141, No.4, pp.315-322, , July 1994.

Wang H and Keerthipala W, Fuzzy-neuro approach to fault classification for transmission line protection, IEEE Transactions on Power Delivery, Vol.13, No.4, October, pp.1093-1104, 1998.

Mo F and Kinsner W, Probabilistic neural networks for power line fault classification, Proceedings of the 1998 11th Canadian Conference on Electrical and Computer Engineering, CCECE, pp585-588, 1998.

Lai, L, Application of neural networks to fault classification and protection, Proceedings of the 1997 4th International Conference on Advances in Power System Control, Operation and Management, p 172-76, 1998.

Aggarwal R, Xuan Q, Dunn R, Johns A and Bennett A, Novel fault classification technique for double-circuit lines based on a combined unsupervised/supervised neural network, IEEE Transactions on Power Delivery, Vol.4, No.4, October, pp.1250-1256, 1999.

Zhao W, Song Y and Min Y, Wavelet analysis based scheme for fault detection and classification in underground power cable systems, Electric Power System Research, Vol. 53, No. 1, pp23-30, 2000.