Keywords
|
| Gravitational Search Algorithm (GSA), Gravitational constant, Induction Motor, Loss minimization, and Torque maximization. |
INTRODUCTION
|
| Within the past few years, many researchers have tended toward optimization-based approaches [1]–[4] for solving equations. The enhanced bee swarm optimization algorithm and self-adaptive modified firefly algorithm are implemented in [1] and [2], respectively, for solving the complex dynamic economic dispatch problem. One of the newest evolutionary algorithms is gravitational search algorithm (GSA), presented by Rashedi et al. in [5]. GSA is extensively used in different optimization problem due to fast convergence and suitability of handling mixed integer problems. |
| Three phase induction motor is used in industrial, commercial, domestic application for several decades. Particularly squirrel cage induction motor is mostly used for this purpose. Thus it is very essential to design efficient induction motor. To get maximum efficiency, losses should be minimized but at the same time torque must be optimum. Regarding the optimization of motor loss and torque the motor parameters i.e. resistances and inductances of the stator and rotor are taken for optimization [6].Initially the expression of torque of an induction motor is maximized with developed Gravitational Search Algorithm, then the expression of loss of an induction motor is minimized. Finally both the torque and loss expression is optimised considering multi-objective optimization of GSA. |
| Standard non-linear programming method can be used to solve these types of problem. But due to its expensive computational time it is rarely used [7-9]. With loss& torque expression it is possible to calculate the optimum value of resistance and inductance. Thus GSA [10] is applied to calculate the parameters for optimization of losses and torque. |
INDUCTION MOTOR EQUIVALENT CIRCUIT
|
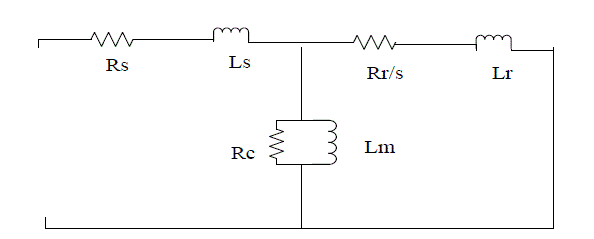
| The equivalent circuit for a three-phase induction motor is shown in Fig.1. Where s represents slip, R_s is the stator resistance, R_r is the rotor resistance, L_s is stator inductance, L_r is rotor inductance. R_c is the core loss resistance which represent core loss of an induction motor & L_m is the mutual inductance. |
PROBLEM DEFINITION AND IMPLEMENTATION USING GSA
|
| The expression of torque and losses are optimized using GSA to get optimum parameter value. Firstly the expression of torque is maximized to get rated torque at a particular voltage. The equation (1) represents the torque equation. |
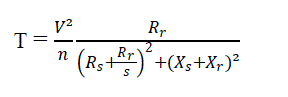 |
| Where Xs = 2πfLs, Xr = 2πfLr, n is synchronous speed. |
| The objective function for torque maximization is given in equation (2) |
| Minimize 1/T (2) |
| Secondly the expression of losses of an induction motor, shown in equation (3) is minimized for a particular voltage. In induction motor stator and rotor copper losses and core loss dominate the overall power losses. Stray, friction and windage losses exist, however they are small enough to be considered negligible. In this case, the total power losses of the motor can be expressed as |
| P_loss= stator copper loss + rotor copper loss + core losses |
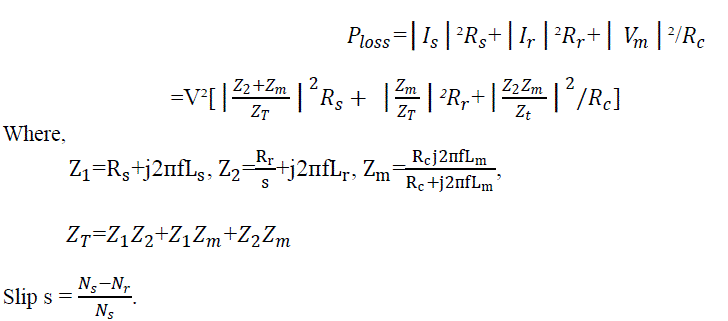 (3) (3) |
| Finally the expression of torque and losses i.e equation (2) and (3) are optimized using proposed algorithm. |
GRAVITATIONAL SEARCH ALGORITHM
|
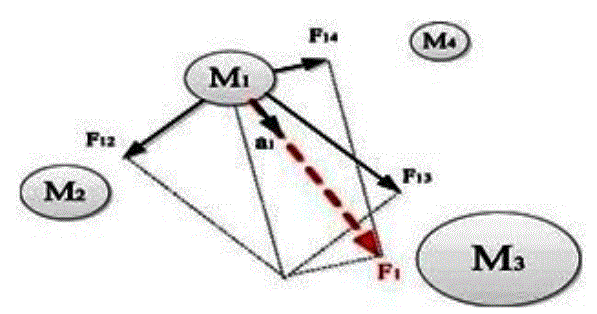
| The Gravitational search algorithm (GSA) is a newly developed stochastic search algorithm based on the law of gravity and mass interactions. In this approach, the search agents are a collection of masses which interact with each other based on the Newtonian gravity and the laws of motion. In the Newton Gravitational Law, each particle attracts other particles with a force known as the Gravitational force [10]. The Fig.2 shows the acceleration vector and force vector of the Newton Gravitational Law, which is used in GSA. In GSA, agents are considered as objects and their performance are measured by their masses. All of the objects attract each other by the gravity force, while this force causes a global movement of all objects towards the objects with heavier masses. The heavy masses correspond to good solutions of the problem. In other words, each mass presents a solution, and the algorithm is navigated by properly adjusting the gravitational and inertia masses. By lapse of time, the masses will be attracted by the heaviest mass which it presents an optimum solution in the search space. The Gravitational search algorithm implementation steps are shown as follows. |
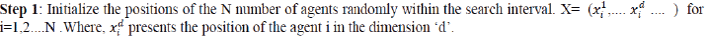 |
 |
 |
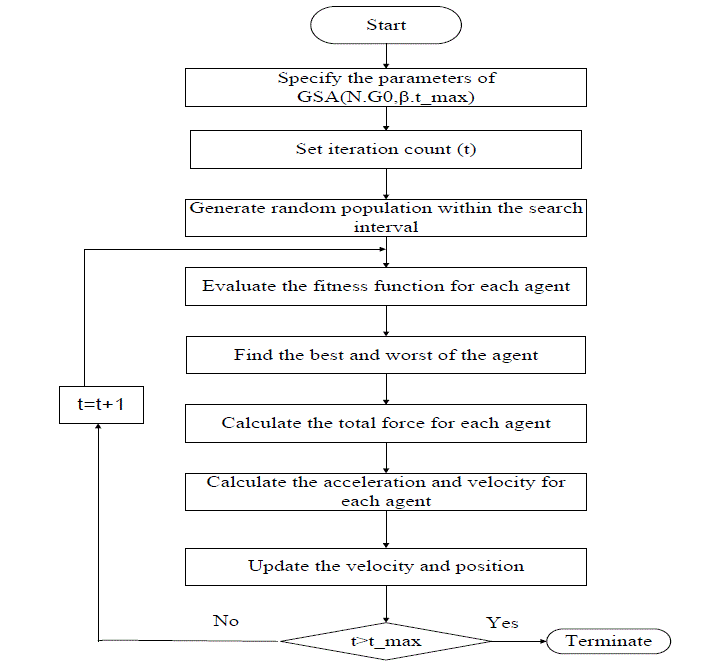
| The flowchart for torque and losses optimisation of three-phase induction motor is shown in Fig. 3. |
SIMULATION RESULTS AND DISCUSSION
|
 |
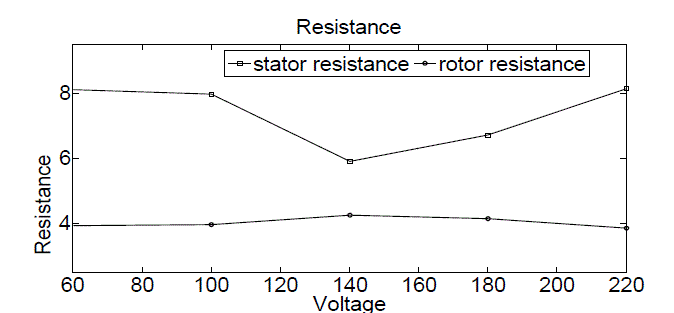
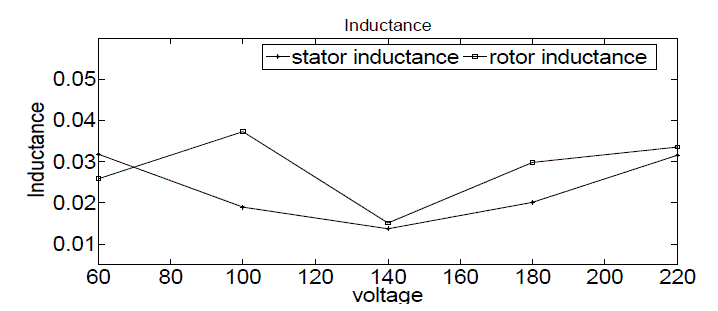
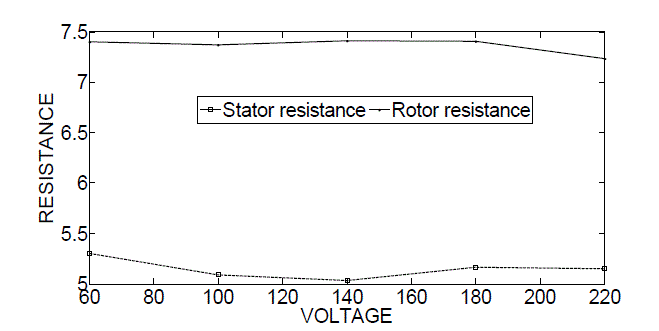
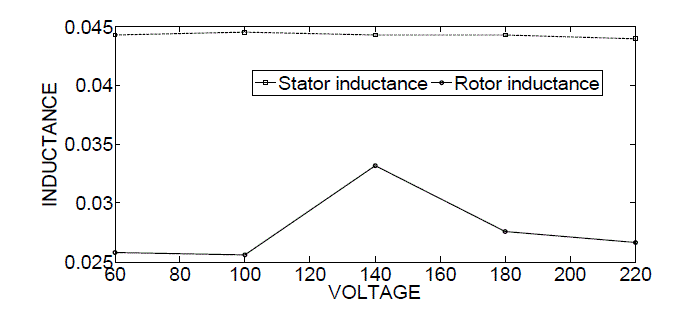
| Fig.4 shows the variation of stator and rotor resistance with varying supply voltage for maximum torque of specified three-phase induction motor. Similarly Fig.5 shows the variation of stator and rotor inductance with varying supply voltage for maximum torque of specified three-phase induction motor. |
| TABLE 3 shows parameters value for minimum losses of specified induction motor using GSA with varying supply voltage. |
| Fig.6 shows the variation of stator and rotor resistance with varying supply voltage for minimum losses of specified three-phase induction motor and Fig.7 shows the variation of stator and rotor inductance with varying supply voltage for minimum losses. |
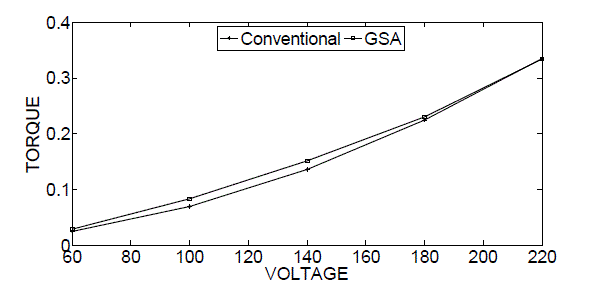
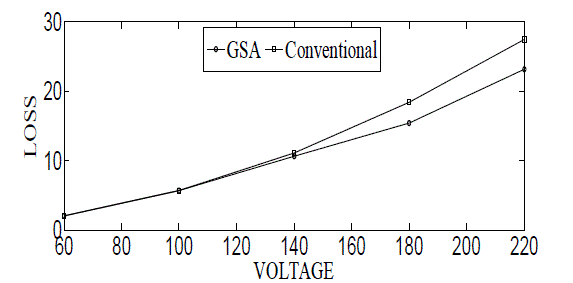
| TABLE 4 shows parameters value for optimum losses and torque of specified induction motor using GSA with varying supply voltage. The torque of a conventional three-phase induction motor is compared with optimal design three-phase induction motor torque and result is shown in Fig.8. Similarly Fig. 9 shows comparative result of losses of a conventional induction motor with optimal design motor. It is no doubt that optimal design motor sows better results than that of a conventional motor. Variation of loss and torque of an optimum design induction motor with supply voltage is shown in Fig. 10. |
CONCLUSION
|
| The torque and losses of an induction motor is optimized using gravitational search algorithm (GSA). The stator resistance, rotor resistance, stator leakage reactance and rotor leakage reactance are calculated using developed GSA. Then torque and loss are calculated using optimum parameters value with varying supply voltage. Torque and loss for optimum values are compared with conventional parameters values. The simulation results shows that torque and loss for optimum values are better than that of conventional values. |
Tables at a glance
|
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
|
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
| |
 |
 |
 |
 |
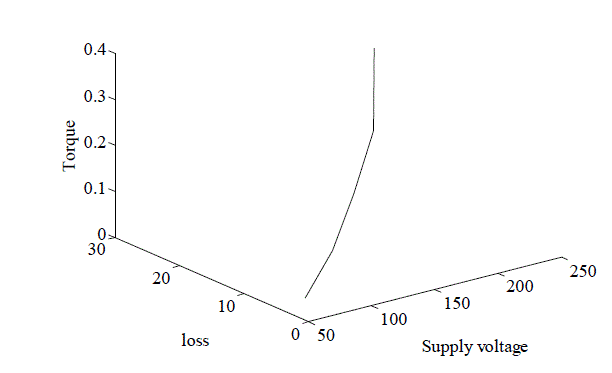 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
Figure 10 |
|
References
|
- T. Niknam and F. Golestaneh, “Enhanced bee swarm optimization algorithm for dynamic economic dispatch,” IEEE Syst. J., doi 10.1109/JSYST.2012.2191831.
- T. Niknam, R. Azizipanah-Abarghooee, and A. Roosta, “Reserve constrained dynamic economic dispatch: A new fast self-adaptive modifiedfirefly algorithm,” IEEE Syst. J., vol. 6, no. 4, pp. 635–646, Dec. 2012.
- Y. Mishra, S. Mishra, and F. Li, “Coordinated tuning of DFIG-based wind turbines and batteries using bacteria foraging technique formaintaining constant grid power output,” IEEE Syst. J., vol. 6, no. 1, pp. 16–26, Mar. 2012.
- F. M. Gonzalez-Longatt, P. Wall, P. Regulski, and V. Terzija, “Optimal electric network design for a large offshore wind farm based on amodified genetic algorithm approach,” IEEE Syst. J., vol. 6, no. 1, pp.164–172, Mar. 2012.
- E. Rashedi, H. Nezamabadi-pour, and S. Saryazdi, “GSA: A gravitational search algorithm,” Info. Sci., vol. 179, no. 13, pp. 2232–2248, 2009.
- S. Sujitjorn and K-L. Areerak, Loss Minimization in an induction Motor Driven by a Voltage –Source Inverter, sin J. Enerjy Environ,Vol 3,Issues 1-2,(2002),pp.53-78.
- Mohammad Khajehzadeh and Mahdiyeh Eslami, Gravitational search algorithm for optimization of retaining structures, Indian Journal ofScience and Technology, vol 5,no 1,Jan 2012.
- Esmat Rashedi, Hossein Nezammabadi, saeid Saryazdi, GSA:A Gravitational Search Algorithm, Information Sciences,179(2009)2232- 2248.
- Mehmet Cunkas, Ramazan Akkaya, Design optimization of induction motor by genetic algorithm and comparison with existing motor. Mathematical and computational applications, Vol 11,No 3,pp.193-203,2006
- M. Eslami, H. Shareef, A. Mohamed, M. Khajehzadeh,” Gravitational search algorithm for coordinated design of PSS and TCSC as damping controller,” Journal of Central South University, vol. 19, no. 4, pp. 923-932, April 2012.
|