A High-Power Propellant-free Electromagnetic Propulsion System Interacting with Local Space-time Curvature

Abstract

This paper proposes a high-power, propellant-free electromagnetic propulsion system grounded in general relativity and nuclear fusion technology. We found that the Riemann cur-nature vanishes and geodesic motion is locally free from gravitational field in a special space-time, demonstrating the feasibility of propellant-free electromagnetic propulsion. To achieve high-power propulsion in a Schwarzschild background, we chose Helmholtz superconducting loop as axis my metric field source and obtain an exact solution to the Einstein-Maxwell field equation using Killing symmetry and Ernst generation technique. An implementation involving a superconductor shield is presented, with Meissner effect calculations implying that the device can be sufficiently free itself from the gravitational field with the aid of existing nuclear fusion engineering.

Keywords

Electromagnetic propulsion; High power; Propellant free; Nuclear fusion

Introduction

The endurance of traditional propellant-consuming aircraft is constrained by the maxi-mum amount of propellant or fuel they can carry. In recent years, various propellant-free propulsion methods such as solar propulsion, antimatter propulsion, and plasma propulsion have been proposed [1, 2]. However, most propulsion mechanics are unclear and are subject to academic controversy and have complex engineering implementations [3].

In 1994, Alcubierre proposed a new type of spaceship drive engine named Alcubierre Drive which is clearly unrealistic as its implementation requires Casimir dark energy [4]. Li Ning et al. observed a weight reduction of 0.5% to 2% in objects floating above a rotating super conducting disk, but they did not provide a rational theoretical explanation [5, 6].

The above studies suggest ideas for new types of propulsion implementation. According to Einstein’s General Relativity, both matter and energy can curve space-time and interact with the background gravitational field [7–9]. In a Schwarzschild background, where the gravitational field is purely generated by matter, introducing powerful electromagnetic energy at some locations necessarily changes the distribution form of the gravitational field. It’s impossible for the effect derived from electromagnetic field curving space-time to happen to eliminate that from pre- existing matter. However, there is a case where, when a free particle is at the point of extreme gravitational potential energy, then its 3-acceleration is zero and the free particle maintains the anti-gravity equilibrium.

This paper will first discuss the phenomenon in which a spacecraft’s geodesic motion is free from gravitational effects and the Riemann curvature vanishes in a special space-time, which demonstrates the feasibility to construct a propellant-free electromagnetic propulsion inter-acting on curvature. Secondly, to achieve high-power propulsion around a Schwarzschild planet like earth, an artificial manifold is introduced in an effective distribution form of static axisymmetric magnetic field, and the requirement to achieve high power is derived from exact solution of Einstein-Maxwell vacuum field equations. Finally, a reasonable implementation is proposed and verified with the aid of the Meissner effect and nuclear fusion engineering techniques.

Materials and Methods

Natural anti-gravity in specific space-time

Reissner-Nordstrom background space time. As summing a spacecraft is placed near the outer surface of the spherically symmetric and uniformly charged planet, at a distance r=r0 from the center. The spacecraft is in the standard Reissner-Nordstrom background space-time, and its line element form is [10].

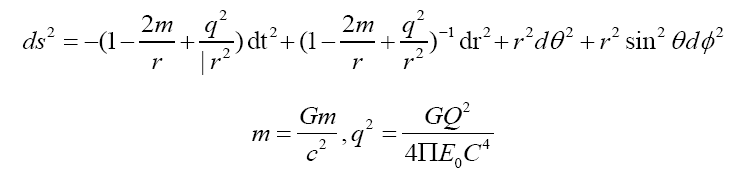
Firstly, approximation of the Newtonian gravitational potential energy with limitation of weak-field and low-velocity has the form as [11].

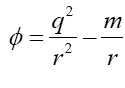
The distribution of the gravitational potential with r corresponding to different charges scalar Q is shown in Figure 1; when Q=0, it degenerates into the Schwarzschild space- time. When Q=0, the gravitational potential has a non-monotonic distribution, and the extreme point of this potential, marked with an asterisk in Figure 1, occurs where r=q2/m. Assume that the low-speed spacecraft is just at the extreme point with zero initial speed, according to the principle of minimum potential energy, 3-space position of the spacecraft should stay the same.

Secondly, assuming that the spacecraft has no charge and its mass is negligible, then its geodesic motion equation is [11].

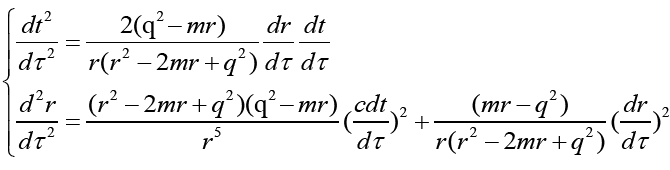
Where symbol c represents the speed of light in vacuum. And the spacecraft starts from the point where r=r0 with a initial velocity of v0=dr/dt=0. When the charge scalar q2=mr0, it is easy to know that its geodesic is a time-like curve and always has.

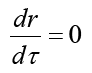
Which implies the spacecraft will keep balance at the point r=r₀, and the gravitational effect of the planet matter will be eliminated by the static electric field.

If given the disturbance to initial velocity, then we can get the evolution law of the spacecraft’s position over coordinate time by numerical simulation in Figure 2. With different initial velocities, the spacecraft vibrates up and down around the balance point r=r0. The amplitude increases as the initial velocity increases.

What’s more, for a given initial velocity, if we assume that the total charge on the planet surface can be controlled artificially according to the position of the spacecraft. Referring to Birkhoff’s theorem and its corollary, the solution is still in form of R-N solution [12]. When the planet’s environment is similar to the Earth, the following control law exists.

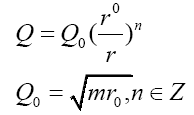
And the larger the n, the stronger the penalty when the spacecraft deviates from the balance point. With a fix initial velocity v0=100 m/s, the spacecraft position varies over coordinate time under the control law given by numerical calculation in Figure 3. It implies that the motion amplitude decreases significantly as the parameter n increase. In general, the initial velocity is much less than 100 m/s, the spacecraft motion under given control law can maintains a good balance at the specified point.

Curvature vanishes locally in special space-time. Static spherically symmetric Weyl solution has a line element as:

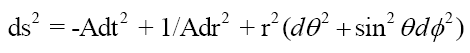
Where A is the function of r with axisymmetric coordinates (t, r, θ, Φ). And all the nonzero components of Riemann curvature tensor are as follows.

It is clear that if there exists r* satisfying following equations.

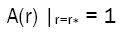
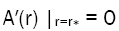
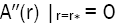
Then all components of Riemann curvature vanish, which means that the space time curvature disappears at this point, and the local space-time becomes Minkowski space-time. In the line element forms given in papers based on the Yukawa effect, A(r) has more than three constant parameters which makes it possible to find a non-singular r' [13–15]. At that point, Riemann curvature tensor vanishes and geodesic motion does get rid of gravitational effect.

In summary, there exists a specific space-time point in the special background space time, where free particles get rid of the gravitational effect or space time degenerates into Minkowski type. Therefore, it is possible to use electro- magnetic field to curve space time and interact on local preexisting gravitational field.

Results

Anti-gravity propulsion in schwarzschild space time

An ordinary planet like earth usually has a spherically symmetric body without electric and magnetic charge. Its outer space-time can be approximately described as a Schwarzschild space-time. In order to realize the anti-gravity effect in this background, it is necessary to generate an energy field which has a more concentrated distribution form than the spherically symmetric R-N field especially in some specific direction.

Field generated by current loop. Neutron stars in the universe possess extremely strong magnetic moments, approximately valued at p~1030G cm³ [16]. Its magnetic field is axisymmetric, and the electromagnetic energy is more concentrated near the polar axis than the spherically symmetric field. Because the magnetic field distribution of a current loop is similar to that of a neutron star, we select the current loop or solenoid as the anti-gravity propulsion source for equipping the spacecraft. Then we will derive the exact metric solution of 4-dimension manifold induced by current loop, some basic assumptions are as follows.

• The initial current strength is near to zero.

• The initial background is the Minkowski space time.

Select the cylindrical coordinates {t, z, ρ, φ}. According to Maxwell equations, components of electromagnetic field are as follows :E_z=E_ρ=E_φ=0,B_φ=0. Nonzero 4-potential vector component: A₃=A_φ.

Now we turn up the current slowly and smoothly, and assume that the current is increased by infinitesimal for each step. The manifold evolves from the Minkowski space time to axisymmetric one. We define the 4-manifold as F (M, g_ab) and metric tensor as g_ab induced by the current loop where the metric satisfies the gauge condition ∇_c g_ab=0. When the current stabilized at a certain level, the curved space-time formed by it is axisymmetric (there is a space-like Killing vector) and static [11]. And the line element can be written in Weyl form [17].

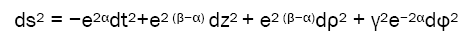
Where α (ρ, z) , β (ρ, z) , γ (ρ, z) are functions of ρ, z. And the Weyl canonical coordinates are noted as {t, z, ρ, φ}. In this paper we use a system of units in which G=c=1, metric signature (−, +, +, +), a spherical coordinate system {t, r, θ, φ}. We also employ an abstract index notation discussed by Penrose, and Latin indices like {a, b, c, d} represent part of notation for tensor itself. Any equation employing Greek indices like {α, β, γ, μ, ν} is a relation between tensor component and specially chosen basis. Weyl canonical coordinates {t, φ} are generated by time-like killing vector ξ a, space-like Killing vector φ^a:

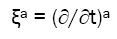
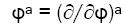
Let K={F_i| i ∈ R} be the homeomorphic set generated during manifold evolution, meanwhile S={Ω_i|i ∈ R} be the space-like hypersurface set induced by orthonormal time-like Killing vector, studies imply that initial constraints is valid to the system throughout the whole evolution, the same is to tensor fields [18, 19]. So we still have A = A3 (ρ, z).

Solution of Maxwell equations: Source-less Maxwell equations in covariant form

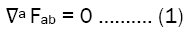
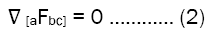
According to study equation (2) is satisfied already with Weyl’s metric form [11]. Eq.1 can be simplified as.

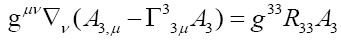
Further simplified: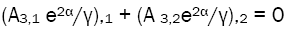

Solutions of Einstein Maxwell equations. Corresponding components of field equation.

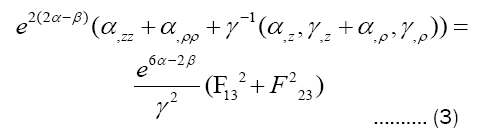
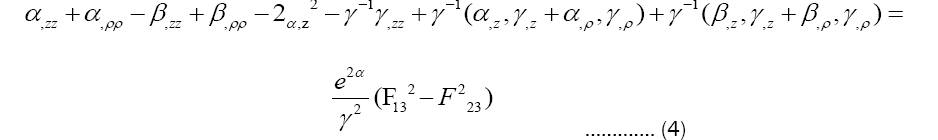
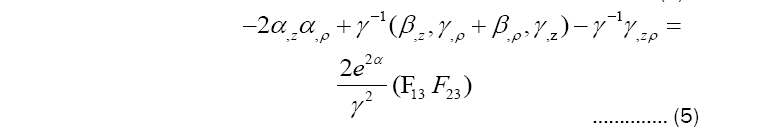
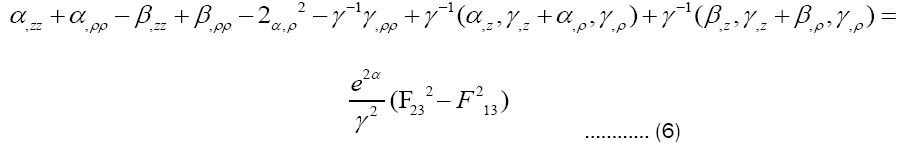
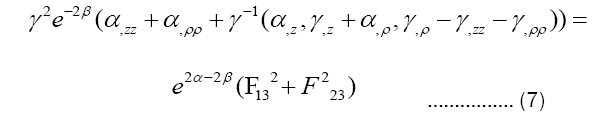
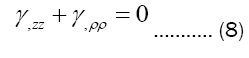
γ is harmonic function of (ρ, z), so it’s reasonable to assume that γ=ρ [19]. (4)+(6) and substitute γ with ρ:

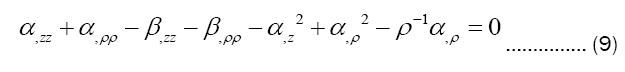
Use eq.9 to simplify (3)-(5):

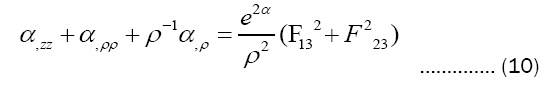
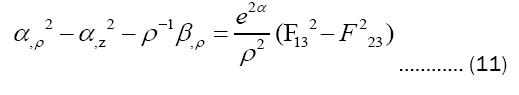
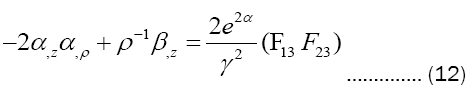
According to equations (11) (12), take substitutions:

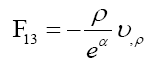
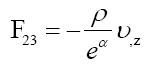
Into Maxwell Equations and use eq.9 to eliminate variable β in equations (10)-(12) (To be convenient commas are omitted in following subscripts):

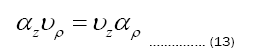
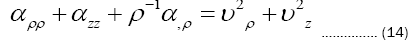
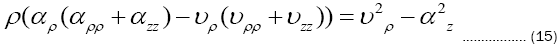
Use equations (13)-(14) to simplify eq.15 [20].

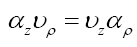
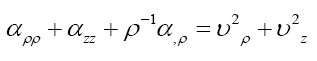
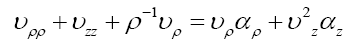
Two class of solutions can be obtained easily:

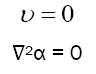
We take the Laplace’s solution in prolate spheroidal coordinate system and have result as follows [21].

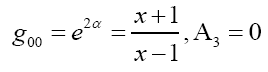
It is the schwarzschild exterior solution.

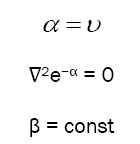
With aid of Ernst generation technique, make substitutions as follows [22].

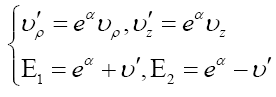
Then field equations have the same form as Ernst equations:

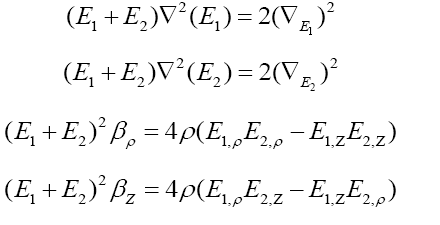
Adopting Ehlers transformation and get solution as [23]

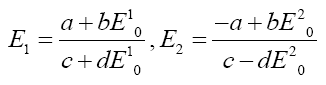
Where a,b,c,d are arbitrary constants. Taking solution (2) as a seed that is:

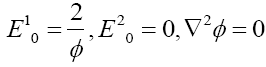
New solutions derived as follows:

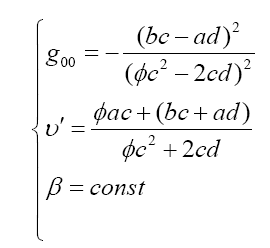
To get the solution matching current loop boundary conditions we take into account the magnetic flux density observed by the ZAMO:

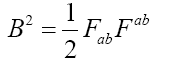
Spatial 3-magnetic components described by the ortho normal tetrad.

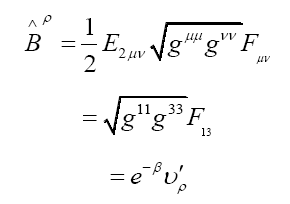
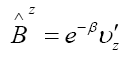
Boundary conditions derived from current loop field in Minkowski space time

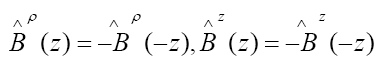
Let β = 0

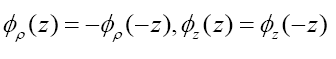
Magnetic flux density’s module:

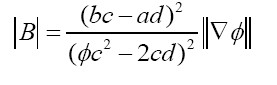
It is convenient to transform coordinates to Weyl spherical coordinate system:

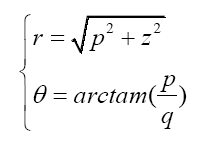
Corresponding line element:

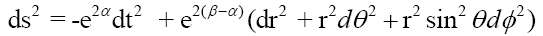
Laplace solution in spherical coordinates:

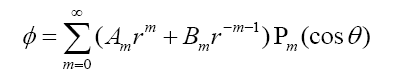
Where Pm represents Legendre’s polynomials, m is a positive integer. Components in different coordinate systems have transformation as follows (left side represents axisymmetric one, while right side represents spherical one):

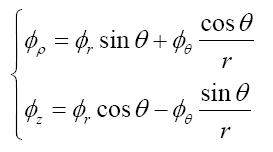
Together with boundary conditions in axisymmetric coordinates, solution has following general form:

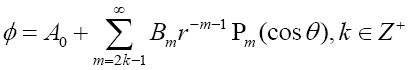
To solve constant parameters, let’s look back to Minkowski space time and magnetic field near to current loop polar axis which has flux density as following form [24].

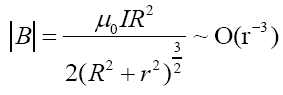
By appending following approximation as conditions:

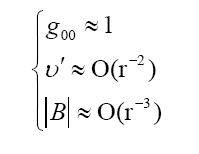
We can derive ϕ and further g₀₀ as follows:

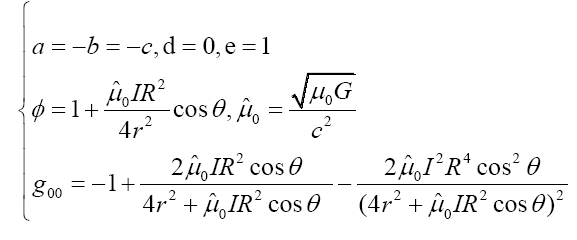
The space time degenerates to Minkowski form as radius goes to infinity.

Current loop in Schwarzschild background: Assume that the current loop is placed around the planet exterior surface, where space time can be described in form of Schwarzschild metric in spherical coordinates {t,r',θ, ϕ}:

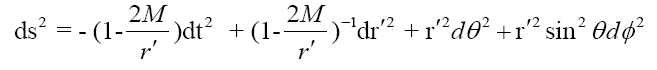
Where r' describes the radius and its origin point is located in the center of planet. The corresponding metric components:

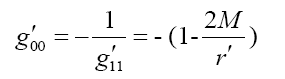
The current loop is placed where r'=R₀ and its polar axis coincides with coordinate axis θ = 0:

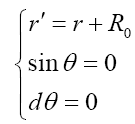
The metric of current loop background space time can be simplified locally as:

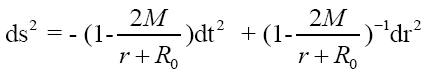
It is clear that symmetry constraints in previous section are not valid anymore except for g₀₀ ≈ g'₀₀ at infinity. Omitting high order terms, the Ernst complex potential solution can be rewritten as:

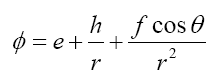
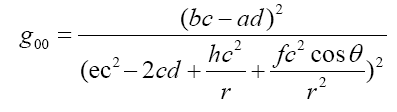
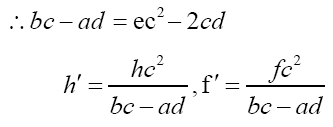
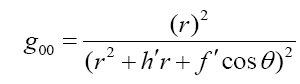
Referring to studies in, the transformation from Weyl axisymmetric coordinate system through pro late spheroidal one to spherical one can be written as [25–27].

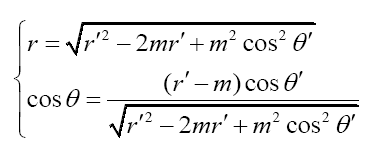
It is clear that θ = 0 around current loop also means θ'= 0:

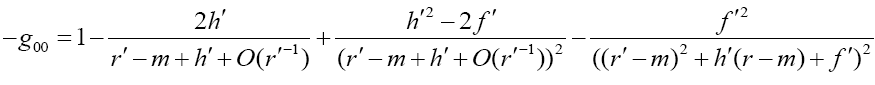
With high order terms omitted, constant parameters are solved as:

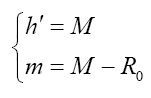
By locally adopting following coordinate’s approximation:

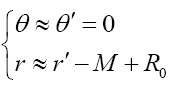
We finally obtain the line element describing the composite gravitational field:

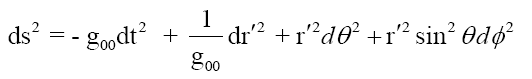
Where:

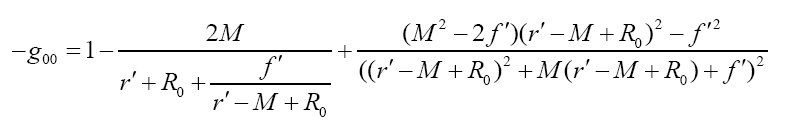
To solve f',let M = 0 and compare magnetic components in different coordinates with notice to the fact that r' −M + R0 ≫ r'. So f' is approximate to:

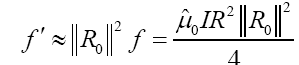
When M ̸= 0 and f'→ 0, curved space time degenerates to Schwarzschild type.

Required source strength for anti-gravity propulsion. Free particle’s geodesic around current loop:

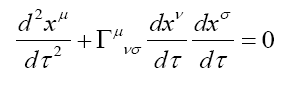
For motion much slower than the speed of light, the proper time may be approximated to the coordinate time as:

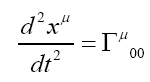
Where

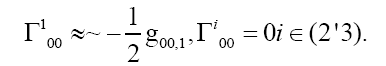
Let

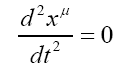
We obtain source strength I where free particle is located at radius r = δ:

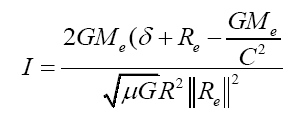
Where μ0 = 1.257 × 10⁻⁶N · A⁻²,G = 6.67 × 10⁻¹¹N · m²/kg², c = 3×10⁸m/s, M_e= 5.965×10²⁴kg, R_e= 6.371× 10⁶m. Let loop radius R and particle position radius δ be unit length, then the result of source strength is:

I = 1.364 × 10¹⁶A

However, it’s still unfeasible to realize such strong current, even with a superconductor limited to critical current density. So following work will be searching a feasible implementation based on superconductor mechanism.

Implementation of high power anti-gravity propulsion.

Discussion

Implementation of high power anti-gravity propulsion

Static magnetic field modulation: Let’s reconsider the form of Laplace’s solution from section 3.3:

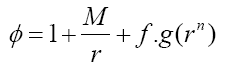
The difference is the third term which represents limitations to some specific boundary conditions. And if we substitute it into geodesic function, the corresponding current can be solved as:

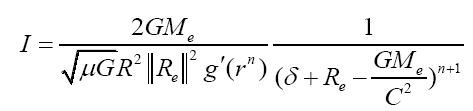
When n = −2, I_c = I₀ = 1.364 × 10¹⁶A. When n =−1, I_c = 2.141 × 10⁹A. Corresponding complex potential vector is:

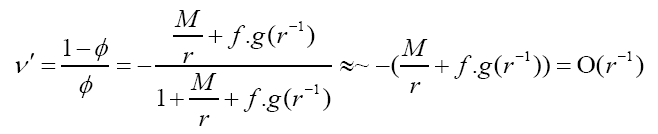
Therefore, it can be concluded that if the magnetic potential vector field can be modulated to vary more slowly with radius, the required current strength can be significantly reduced.

Taking into account the Meissner effect of superconductors, an implement is shown in Figure 4 [28].

Qualitatively, according to the Meissner effect, total magnetic flux in the central region surrounded by A-A’ and B-B’ does not change over the z-coordinate:

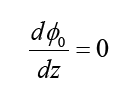
Assume that the curve shape of s1-s2 is described by: ρ=f (z) The average magnetic flux density over z is:

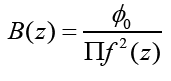
It is clear that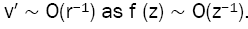 Quantitatively, consider the magnetic flux density of the Helmholtz coil in the ρ − z coordinate system:

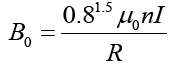
Take a slice of B-B’ at position z=0 to study as shown in figure. Inside the body of superconductor B-B’, according to London equations and Maxwell equations we can obtain the compound magnetic flux density where ρ=0, z =δ → 0 assumed that boundary field maintains continuity [29].

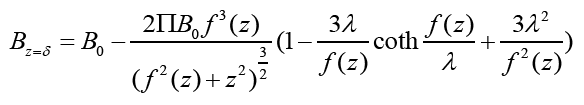
Because f (z) >> λ:

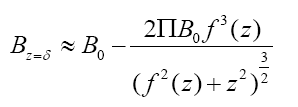
If given f (z)=z^2/3, then B_z=δ=O(z⁻¹). So the magnetic field can be modulated by adjusting the shape of the curve. Therefore the current intensity required to counteract the background gravity is significantly reduced. In fact, if the central region of Helmholtz coil is filled with dielectric but magnetically conductive material, then its relative permeability will be about10⁴~10⁵ and current could be reduced to 2.141 × (10⁶~10⁷)A. According to study the single Toroidal Field Coil of CFETR (nuclear fusion tokamak device) can bear about1.47 × 10⁷A. Therefore the proposed implement and method is feasible [30].

Conclusion

This paper discusses the limitations of conventional electromagnetic propulsion and proposes a high-power, propellant-free propulsion system that locally interacts with the background space-time curvature. To achieve effective propulsion, a prototype consisting of a Helmholtz superconducting coil and superconductor shield is proposed. Computation demonstrated the feasibility of effective interaction on the gravitational field. Detail control techniques need to be processed in further work.

References

1. Meyer M, et al. National Aeronautics and Space Administration. 2023.

   [Google scholar]

2. Frisbee R H. Advanced space propulsion for the 21st century. J. Propuls. Power. 2023;19:1129-1154.

   [Crossref][Google scholar]

3. Millis M. Assessing potential propulsion breakthroughs. Ann. N. Y. Acad. Sci. 2005;1065: 441–461.

   [Crossref][Google scholar][Pubmed]

4. Alcubierre M. The warp drive: hyper-fast travel within general relativity. ISO4. 1994;11: L73–L77.

   [Crossref][Google scholar]

5. LI N, et al. Static test for a gravitational force coupled to type II YBCO superconductors. Phys. C: Supercond. Appl. 1997;281:260-267.

   [Crossref][Google scholar]

6. Koczor R, et al. Fabrication of large bulk ceramic superconductor disks for gravity modification experiments and performance of YBCO disks under EM field excitation. ARC. 1999.

   [Crossref][Google scholar]

7. Reissner H. Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie . Ann. Phys. 1916;355:106-120.

   [Crossref][Google scholar]

8. Newman E, ET AL. Metric of a rotating, charged mass . J. Math. Phys. 1965;6: 918-919.

   [Crossref][Google scholar]

9. Tsagas C. Magnetic fields in conformally flat spacetimes. J. Phys. Conf. Ser. 2007;68:12-51.

   [Crossref][Google scholar]

10. Nordstrom G., Proceedings series b physical sciences. Proc. Jpn. Acad., Ser. B, Phys. 1918:1201–1208.

    [Google scholar]

11. Canbin L, ET AL. Introduction to differential geometry and general relativity. Springer Sci. Rev. Science Press, Beijing. 2006;1:78-230.

    [Google scholar]

12. Carmeli M. Classical fields: general relativity and gauge theory. John Wiley Sons, New York. 1982;70-669.

    [Google scholar]

13. Stephenson G. A static spherically symmetric solution of the Einstein—Maxwell—Yukawa field equations. Math. Proc. Camb. Philos. Soc. 1962;58: 521-526.

    [Crossref][Google scholar]

14. Kruglov S. I. Corrections to Reissner-Nordström black hole solution due to exponential nonlinear electrodynamics.EPL. 2016;115:60006.

    [Crossref][Google scholar]

15. Mazharimousavi S. H, et al. Einstein-nonlinear Maxwell–Yukawa black holeInt. J. Mod. Phys. D. 2019;28:1950120.

    [Crossref][Google scholar]

16. Popov S. Evolution of isolated neutron stars. Springer Sci. Rev. 2001;44:101-110.

    [Crossref][Google scholar]

17. Weyl H., Zur Gravitations theorie .ADP. 1917;359:117-145.

    [Crossref][Google scholar]

18. Canbin L, ET AL. Introduction to differential geometry and general relativity. Springer Sci. Rev. Science Press, Beijing. 2006;1:78-230.

    [Google scholar]

19. Wald R., General Relativity(University of Chicago Press,Chicago). 1984: 252-254.
20. Turimov B, et al. General relativistic effects in neutron star electrodynamics. Phys. Rev.D. 2021;103: 124039.

    [Crossref][Google scholar]

21. Gutsunave T, et al. On the gravitational field of a mass possessing a multipole moment. Springer Sci. Rev. 1985;17:1025-1027.

    [Crossref][Google scholar]

22. Ernst F J. New formulation of the axially symmetric gravitational field problem. Phys. Rev. E. 1968;167:1175.

    [Crossref][Google scholar]

23. Banerjee A, et al. Ehlers transformations as EM duality in the double copy. Phys. Rev.D, 2020;102:126017.

    [Crossref][Google scholar]

24. Jackson D. Classical Electrodynamics. Wiley,New York. 1999.

    [Google scholar]

25. Gutsunave T I, et al. On the gravitational field of a mass possessing a magnetic dipole moment. A isPhys. Let. 1987;123: 215-216.

    [Crossref][Google scholar]

26. Gutsunaev T I, et al. On a family of solutions of the Einstein-Maxwell equations. Springer Sci. Rev. 1988;20:327-335.

    [Crossref][Google scholar]

27. Gutsunave T I, et al. New stationary electrovacuum generalizations of the Schwarzschild solution. Phys. Rev. D. 1989;40:2140.

    [Crossref][Google scholar]

28. Meissner W,et al., Ein neuer Effekt bei Eintritt der Supraleitfähigkeit. Springer Sci. Rev. 1933;21:787–788.

    [Crossref][Google scholar]

29. Yuheng Z., Superconducting Physics (University of Sci- ence and Technology of China Press,Hefei) 2009; 54-56.
30. LIU X G, et al. Nuclear Fusion, 2020; 60:046032.