INTRODUCTION
|
| The voltage-power characteristic of a photovoltaic (PV) array is nonlinear and time varying because of the changes caused by the atmospheric conditions. The task of a maximum power point (MPP) tracking (MPPT) in a PV power system is to continuously tune the system so that it draws maximum power from the PV array.In recent years, the grid connected PV systems have become more popular because they do not need battery backups to ensure MPPT. The two typical configurations of a grid-connected PV system are single or two stages. In two stages, the first is used to boost the PV array voltage and track the maximum power; the second allows the conversion of this power into high-quality ac voltage. |
| The presence of several power stages undermines the overall efficiency, reliability, and compactness of the system besides increasing the cost. The single stage has numerous advantages, such as simple topology, high efficiency, etc. Nevertheless, the control strategy (FZZY Logic) has to be designed in order to extract the maximum available power and to properly transfer it from the PV array to the grid simultaneously. In this case, an important consideration in the controller design is needed. |
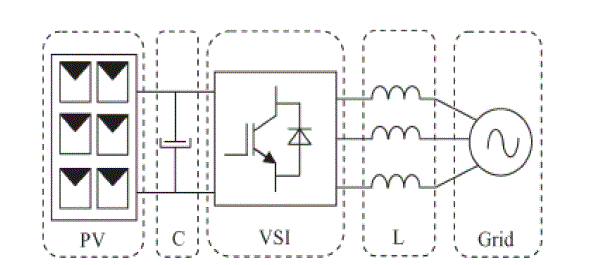
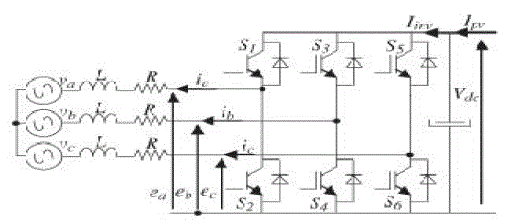
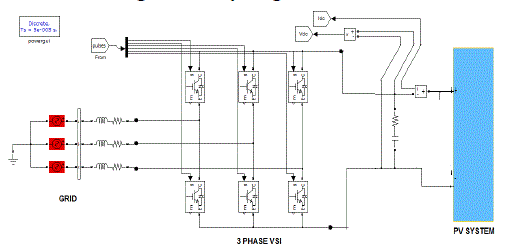
| In this paper, the main component of the single-stage grid connected PV system is the three-phase voltage source inverter (VSI). Typically, simple inductors L are used as a filter interfacing inverter and mains, as shown in Fig. 1. LCL filter provides advantages in costs and dynamics since smaller inductors can be used. However, in a grid-connected system, an LCL filter may cause resonance, which is a disaster for the system’s stability. Hence, control systems involving LCL filters are inevitably more complicated. The voltage-oriented control (VOC) method used for VSI employs an outer dc link voltage control loop and an inner current control loop to achieve fast dynamic response. The performance of the power flow depends largely on the quality of the applied current control strategy. In this paper, the current control has been implemented in a rotating synchronous reference frame d, q because the controller can eliminate a steady-state error and has fast transient response by decoupling control. |
| Many algorithms have been developed for the MPPT of a PV array. Among the MPPT techniques, the perturbation and observation (P&O) method is the most popular because of the simplicity of its control structure. Yet, in the presence of rapidly changing atmospheric conditions, the P&O MPPT algorithm can be confused due to the fact that it is not able to distinguish the variations of the output power caused by the tracker perturbation from those caused by the irradiance variation. Recently, improved P&O MPPT algorithms for rapidly changing environmental conditions have been proposed by Sera et al. In this paper, in order to generate the correct MPP reference voltage under rapidly changing irradiation, a robust MPPT controller has been proposed. In this algorithm, the d-axis grid current component reflecting the power grid side and the signal error of a FUZZY Logic controller instead of PI controller outer voltage regulator is designed to reflect the change in power caused by the irradiation variation. Hence, with this information, the proposed algorithm can greatly reduce the power losses caused by the dynamic tracking errors under rapid weather changing conditions. The superiority of the newly proposed method is supported by simulation and experimental results. |
SYSTEM DESCRIPTION AND MODELING
|
| Fig. 1 shows the basic structure of a single-stage three-phase grid-connected PV system studied in this paper. This system consists of a PV array, an input filter capacitor C, a three-phase VSI, an output filter inductor L, and grid. The PV modules are connected in a series–parallel configuration to match the required dc voltage and power rating. The input capacitor supports the solar array voltage for the VSI. The three-phase pulse width-modulated inverter with a filter inductor converts a dc input voltage into an ac sinusoidal voltage by means of appropriate switch signals to make the output current in phase with the utility voltage and obtain a unity power factor. |
A. Solar Cell and PV Array Model
|
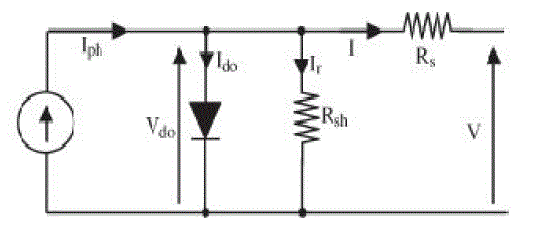
| A PV generator is a combination of solar cells, connections, protective parts, supports, etc. In the present modeling, the focus is only on cells. Solar cells consist of a p-n junction; various modeling’s of solar cells have been proposed in the literature. Thus, the simplest equivalent circuit of a solar cell is a current source in parallel with a diode. The output of the current source is directly proportional to the light falling on the cell (photocurrent). During darkness, the solar cell is not an active device; it works as a diode, i.e., a p-n junction. It produces neither a current nor a voltage. Thus, the diode determines the I–V characteristics of the cell. For this paper, the electrical equivalent circuit of a solar cell is shown in Fig. 2 The output current I and the output voltage of a solar cell are given by |
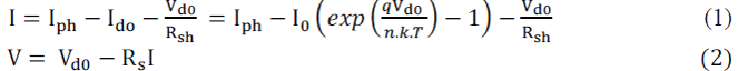 |
| Here, Iph is the photocurrent, I0 is the reverse saturation current, Ido is the average current through the diode, n is the diode factor, q is the electron charge (q = 1.6*10-19), k is VSI. |
| the Boltzmann’s constant (k = 1.38*10−23), and T is the solar array panel temperature. Rs is the intrinsic series resistance of the solar cell; this value is normally very small. Rsh is the equivalent shunt resistance of the solar array, and its value is very large. In general, the output current of a solar cell is expressed by |
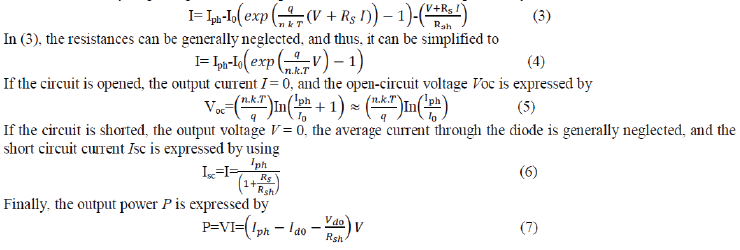 |
VSI MODEL
|
| The VSI connected to the grid through an L filter is shown in Fig. 3. In this section, a dynamic analytical model of the VSI is developed in its original three-phase abc frame. Then, this model is transformed into a synchronous reference frame. Before analyzing the three-phase VSI, some assumptions are proposed. The three-phase voltages are sinusoidal and symmetrical, and their representations are depicted in (8).The switches operate at constant frequency. The switching frequency is much higher than the line frequency. The inductors L are linear and balanced. Saturation is not a concern. |
| 1) The whole conduction losses are represented by three symmetrical resistors R, as shown in Fig. 3.The absence of the zero sequence in the currents into a three wire system. |
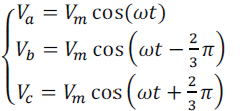 (8) (8) |
| Based on the aforementioned assumptions, the model of the VSI in the stationary abc frame is established as |
 |
| For pulse width modulation (PWM) inputs, the aforementioned model can be separated into low- and high-frequency components using the Fourier analysis. The high-frequency model is concerned with the switching behavior of the inverter and is almost neglected. The low-frequency model, which has the same expression as (12), with the switching functions d* being replaced by continuous duty ratios dk(k = 1, 3, 5) ∈ [0, 1], is much more considered |
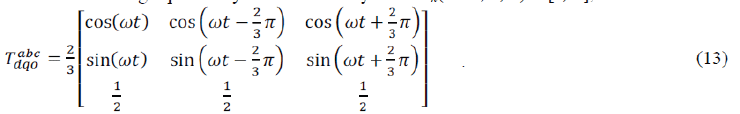 |
| It is noted that the model (12) is time varying and nonlinear. In order to facilitate the control, the model can be transformed into a synchronous orthogonal frame rotating at the angular frequency of the utility ω. With this timevarying transformation, given by (13), the positive sequence components at the fundamental frequency become constant.Finally, the whole dynamic model (14) in the dq frame is obtained from (12) and (13) |
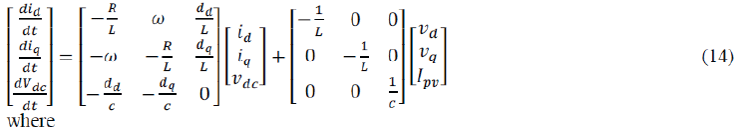 |
| id, iq d- and q-axis grid currents, respectively; νd, νq d- and q-axis grid voltages, respectively; dd, dq d- and qaxis duty ratios. |
3.1 Current And Voltage Controllers
|
| According to [19], VOC strategy guarantees fast transient response and high static performance via internal current control loops. |
A. Current Control
|
| It can be seen from (14) that there is cross-coupling between the d and q components. However, cross-coupling can affect the dynamic performance of the regulator. Therefore, it is very important to decouple the two axes for better performance. This effect can be accomplished with the feed forward decoupling control method. Assuming that |
| vrd = -vd+ddvdc+ωLiq |
 |
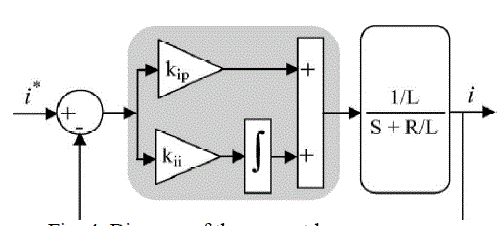
| The cross-coupling variables are eliminated in the aforementioned model. Hence, the currents id and iq can be controlled independently by acting upon inputs Vd and Vq, respectively. Furthermore, by using PI-type regulators, a fast dynamic response and zero steady-state errors can be achieved. The diagram of the current regulator is shown in Fig. 4. Since the switching frequency is much higher than the line frequency, the sampling and hold delay is neglected. the diagram, kip and kii are the proportional and integral parameters, respectively; i* is the reference current signal, and I is the feedback current. The diagram is suitable for both id and |
| iq loops. From the diagram, the closed-loop transfer function of the d, q current loops is |
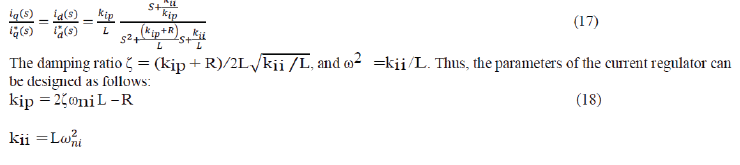 |
B. Voltage Control
|
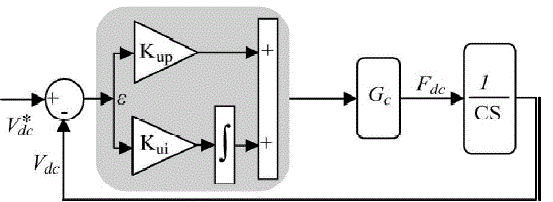
| In the case of a unity power factor (iq= 0) and with the previous assumption, the third equation in the model (14) is repeated as |
 |
| The closed-loop transfer function of dc voltage regulation, obtained from Fig. 5, has the following form: |
 |
3.2 MPPT
|
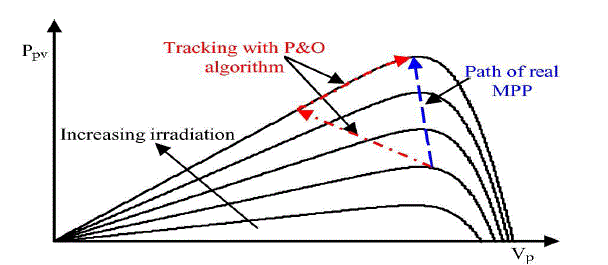
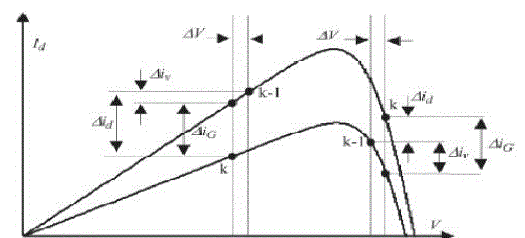
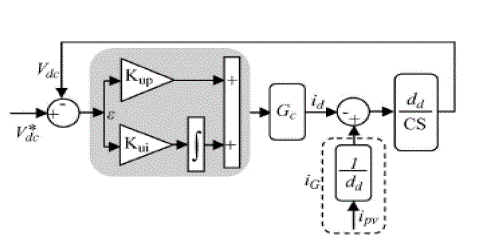
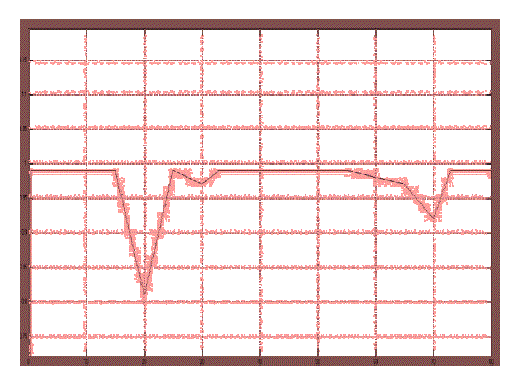
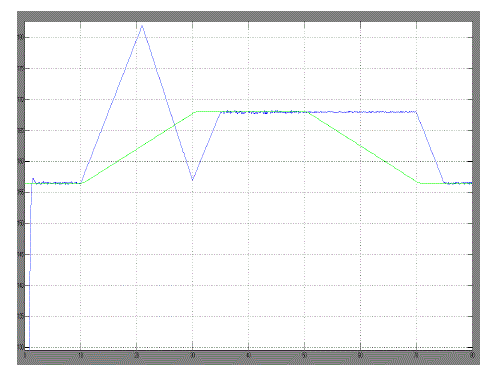
| The dc voltage controller is used to produce the reference current value for the id current controller. Its aim is to keep the voltage constant on the dc side in normal condition or during rapidly changing atmospheric conditions. The MPPT algorithm modulates the reference voltage V ∗ dc according to the environmental conditions in order to keep the operating point of the PV panels close to the MPP. In the conventional P&O method, the MPP is obtained from the PV array power by multiplying the voltage and current of PV arrays and comparing it with the previously measured power. In the case of a sudden increase in irradiance, the P&O algorithm reacts as if the increase occurred as a result of the previous perturbation of the array operating voltage. The next perturbation, therefore, will be in the same direction as the previous one. Assuming that the system has been initially oscillating around the MPPT, the path of this behavior is drawn in Fig. 6. It can be seen that a continuous perturbation in one direction will lead to an operating point far away from the actual MPP. This process continues until the increase in irradiance slows down or ends. |
| The MPPT controller is applied to the reference of the outer loop control dc voltage photovoltaic (PV).Without PV array power measurement, the proposed MPPT identifies the correct direction of the MPP by processing the d-axis current reflecting the power grid side and the signal error of the FUZZY outer loop designed to only represent the change in power due to the changing atmospheric conditions. The robust tracking capability under rapidly increasing and decreasing irradiance is verified experimentally with a PV array emulator. To overcome the limitations of the P&O method, the proposed MPPT enables us to decouple the change in power caused by the simultaneous increment perturbation and irradiation variation. The irradiation variation is estimated by using the signal error of the PI controller of the dc voltage control. The PI regulator is designed to assure zero signal error if the atmospheric conditions are constant and a constant signal error in the opposite case. Hence, the signal error reflects only the change in power caused by the irradiation variation. After that, in order to calculate the total change in the PV array power, the d-axis grid current component is used. Finally, the change in power caused by the previous perturbation is obtained by a simple subtraction; therefore, the correct direction of the MPP can be identified. |
A. PV Power Calculation
|
| In the synchronous rotating frame d, q, the active and reactive powers of a three-phase grid-connected VSI are given by |
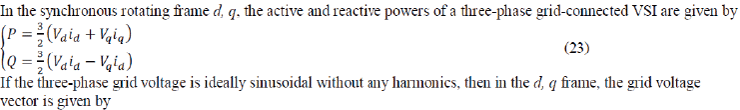 |
 |
| Assuming lossless power transmission between solar array and grid line, the relationship of instantaneous active power exchanged between the PV array and the grid is given by |
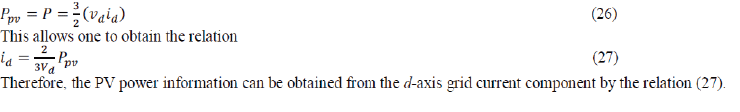 |
B. Signal Error of Outer Voltage Regulator
|
| The change of d-axis current in one period sampling Te under irradiation variation is expressed by the following: |
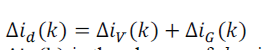 (28) (28) |
| Δiv(k) is the change of d-axis current component caused by the tracker perturbation, and Δiïÿýïÿý(k)is the change of d-axis current component caused by the change in irradiation Fig. 7. Thus, the dc bus-voltage control loop under changing irradiation can be modeled with the block diagram of Fig. 8, where the current of PV array is an input disturbance. In this case, the error |
| between voltage reference V*dc and voltage measurement Vdc is the following: |
 |
 |
| To calculate the signal error, we use the final value theorem for Laplace transforms. According to this theorem, as long as ε(s) |
| does not have any poles in the right half of the complex plane, except maybe s = 0, then |
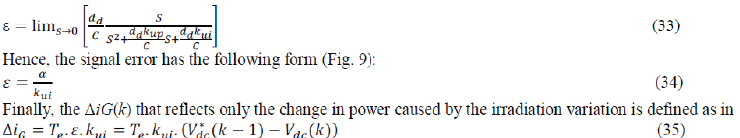 |
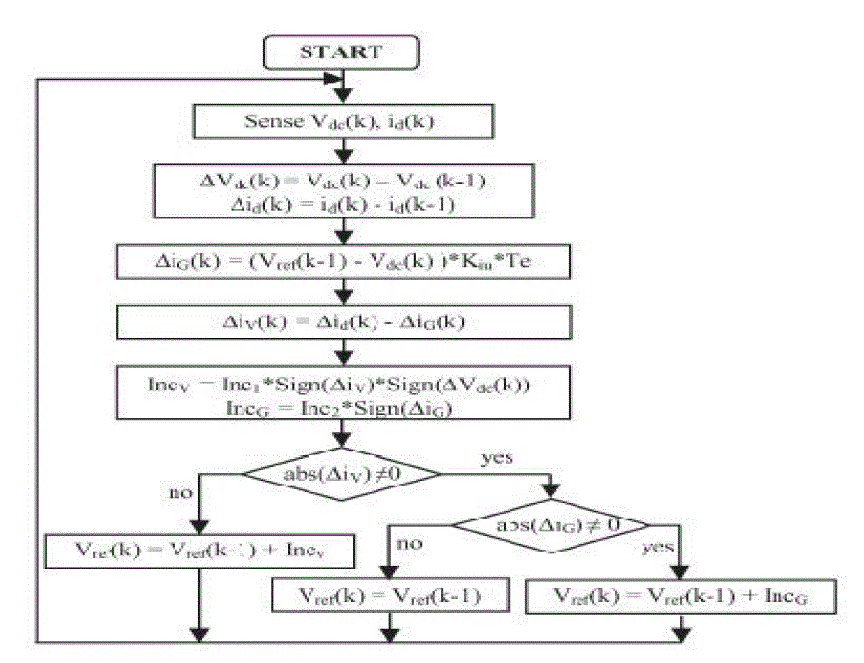
| The flowchart of the proposed MPPT is shown in Fig. 9. The first step is to set up a fixed voltage whose value is about 0.8 times of the PV array open-circuit voltage. Then, the instantaneous voltage of the PV array and the d-axis grid current component are measured using the saved previous voltage and current in order to calculate the differential values of Δid and ΔVdc. After that, the ΔiG and ΔiV are calculated by using (35) and (28), respectively. With this information, two increments are calculated. The first IncV will be used when the PV array voltage is far away from the MPP voltage and the second IncG when irradiance change is present and the PV array voltage is initially equal to the voltage of the MPP. In the next test, if abs(ΔiV ) is more than zero (the power change caused by the previous tracker perturbation is different from zero), the reference voltage of the PV array is given by adding IncV to the previous reference voltage (IncV can be positive or |
MODELLING OF CASE STUDY AND SIMULATION RESULTS
|
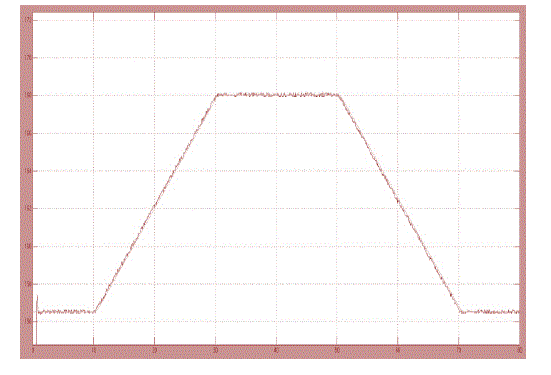
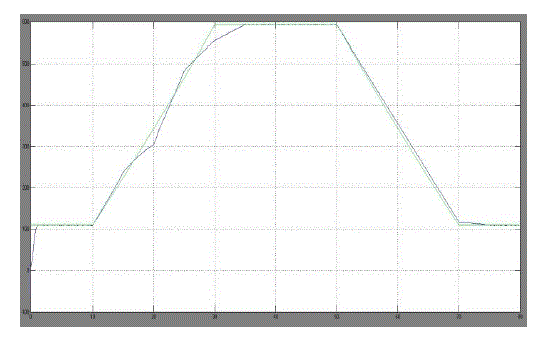
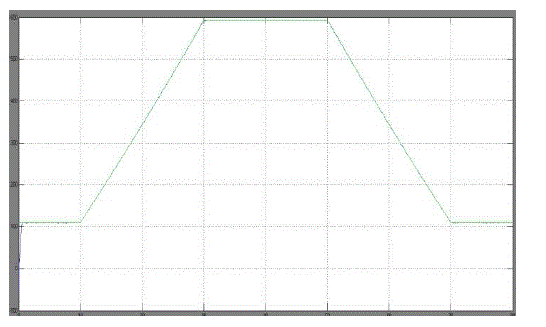
| From the above simulated results we can identify the instantaneous efficiency with modified MPPT using FUZZY Controller , PV system voltage with the modified MPPT and theoretical MPP voltage during a trapezoidal irradiation profile and PV array power during a trapezoidal irradiation profile using the classical P&O MPPT method, compared to the theoretical MPP power are improved. |
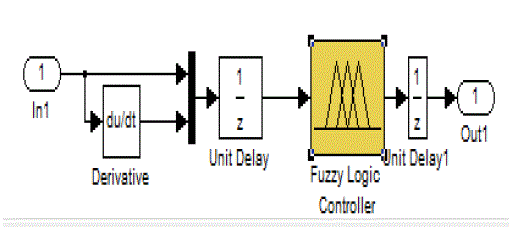
| Fuzzy logic control circuit is implemented in MAT LAB is shown in below fig. |
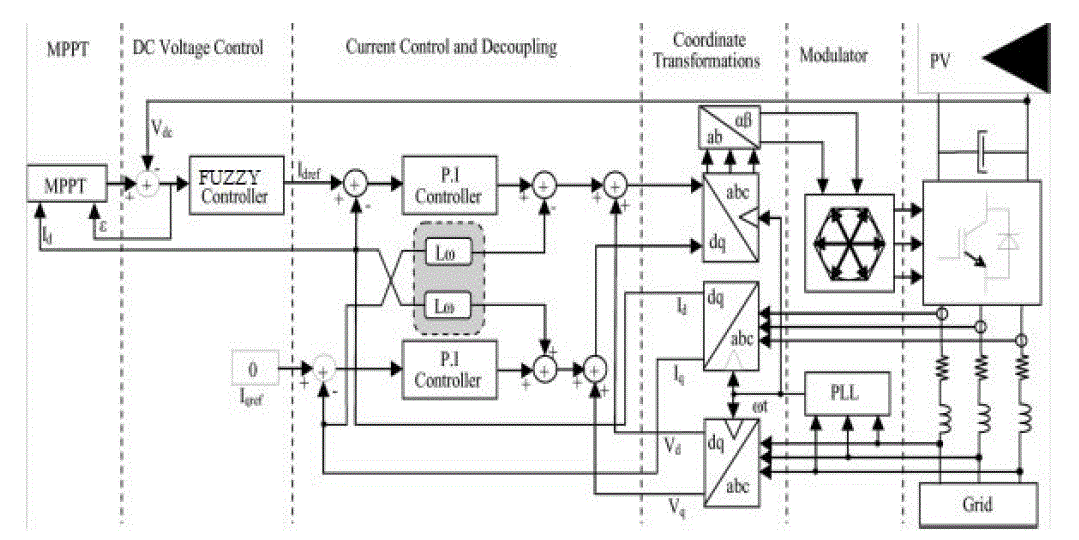
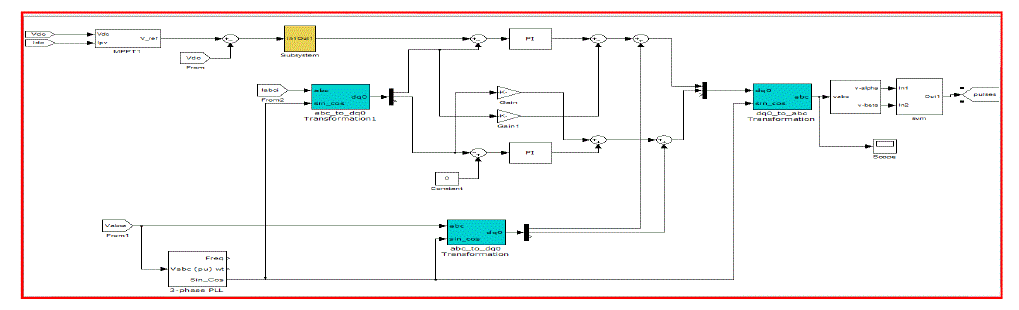
| This section presents the simulation results of the classical P&O and the proposed method in order to validate the performance of the control scheme. Computer simulation has been done using MATLAB/SIMULINK simulation package. The full diagram of the control methodology and the modulation is shown in Fig. 10. The characteristics of Solar PV module are used for the PV array model in the simulation and experiment. The 60 module provides 60 W of nominal maximum power and a 21.1-V open-circuit voltage at an irradiation of 1 kW/m2 and an ambient temperature of 25 âÃâæC. To compare the performance of the proposed MPPT method with that of the P&O method, the simulations are configured under exactly the same conditions to compare the performances. The PV array in simulation is composed of ten series connected modules. The sampling period used for MPPT algorithm is chosen as 0.2 s, and voltage increments of Inc1 = 0.5 V and Inc2 = 0.1 V are used.In order to verify the effect of rapidly changing irradiation, an irradiation ramp change was used. A 20-s period for the increasing and decreasing ramps was selected. This irradiation change starts from 200 W/m2, stops at 1000 W/m2, waits at this level for 20 s, and decreases again back to 200 W/m2 with a constant slope. The temperature is considered constant during the simulation. |
CONCLUSION
|
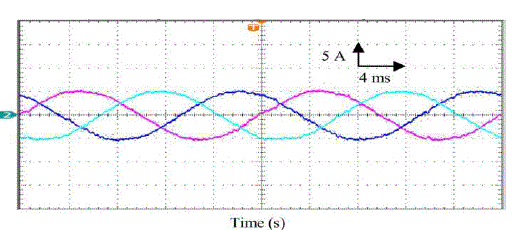
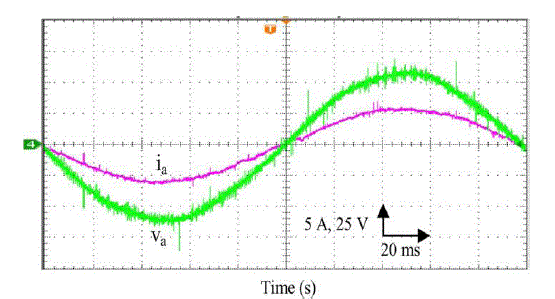
| In order to avoid possible mistakes of the classical MPPT algorithm with PI control due to the fast-changing irradiation, this paper a FUZZY based MPPT-SRF Configuration of a Single Stag Grid-Connected PV System Inverter Based On Voltage-Oriented Control has proposed an improved MPPT controller. Our control scheme uses the d-axis grid current component and the signal error of the FUZZY outer voltage regulator. This MPPT method permits one to differentiate the contribution of increment perturbation and irradiation change in power variation, hence identifying the correct direction of the MPP. In the simulation and experimental results, the robust tracking capability under rapidly increasing and decreasing irradiance has been proved. Moreover, the output power losses caused by the dynamic tracking errors are drastically reduced, particularly under fast changing irradiation. With proposed fuzzy controller we achieved improved wave shapes in ac voltages and also maintain unity power factor. |
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
Figure 10 |
 |
 |
 |
 |
 |
| Figure 11 |
Figure 12 |
Figure 13 |
Figure 14 |
Figure 15 |
 |
 |
 |
 |
 |
| Figure 16 |
Figure 17 |
Figure 18 |
Figure 19 |
Figure 20 |
 |
| Figure 21 |
|
References
|
- RiadKadri, Jean-Paul Gaubert, Member, IEEE, and Gerard Champenois, Member, IEEE “An Improved Maximum Power Point Tracking forPhotovoltaic Grid-Connected Inverter Based on Voltage-Oriented Control” IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, VOL. 58,NO. 1, JANUARY 2011
- C. Meza, J. J. Negroni, D. Biel, and F. Guinjoan, “Energy-balance modeling and discrete control for single-phase grid-connected PV centralinverters,” IEEE Trans. Ind. Electron., vol. 55, no. 7, pp. 2734–2743, Jul. 2008.
- B. Sahan, A. N. Vergara, N. Henze, A. Engler, and P. Zacharias, “A singlestage PV module integrated converter based on a low-powercurrentsource inverter,” IEEE Trans. Ind. Electron., vol. 55, no. 7, pp. 2602–2609, Jul. 2008.
- K. Hemmes, “Towards multi-source multi-product and other integrated energy systems,” Int. J. Integr. Energy Syst., vol. 1, no. 1, pp. 1–15, Jan.–Jun. 2009.
- F. Liu, Y. Zhou, S. Duan, J. Yin, B. Liu, and F. Liu, “Parameter design of a two-current-loop controller used in a grid-connected inverter systemwith LCL filter,” IEEE Trans. Ind. Electron., vol. 56, no. 11, pp. 4483–4491, Nov. 2009.
- T. Shimizu, O. Hashimoto, and G. Kimura, “A novel high-performance utility-interactive photovoltaic inverter system,” IEEE Trans. PowerElectron., vol. 18, no. 2, pp. 704–711, Mar. 2003.
- T. Esram, J. W. Kimball, P. T. Krein, P. L. Chapman, and P. Midya, “Dynamic maximum power point tracking of photovoltaic arrays using ripplecorrelation control,” IEEE Trans. Power Electron., vol. 21, no. 5, pp. 1282–1291, Sep. 2006.
- N. Femia, G. Petrone, G. Spagnuolo, andM. Vitelli, “Optimization of perturb and observe maximum power point tracking method,” IEEE Trans.Power Electron., vol. 20, no. 4, pp. 963–973, Jul. 2005.
- G. Carannante, C. Fraddanno, M. Pagano, and L. Piegari, “Experimental performance of MPPT algorithm for photovoltaic sources subject toinhomogeneous insolation,” IEEE Trans. Ind. Electron., vol. 56, no. 11, pp. 4374–4380, Nov. 2009.
- N. Femia, G. Petrone, G. Spagnuolo, and M. Vitelli, “Perturb and observe MPPT technique robustness improved,” in Proc. IEEE Int. Symp. Ind.Electron., 2004, vol. 2, pp. 845–850.
- K. H. Hussein, I. Muta, T. Hoshino, and M. Osakada, “Maximum photovoltaic power tracking: An algorithm for rapidly changing atmosphericconditions,” Proc. Inst. Elect. Eng.—Gener.,Transm. Distrib., vol. 142, no. 1, pp. 59–64, Jan. 1995.
- N. Femia, G. Petrone, G. Spagnuolo, and M. Vitelli, “A technique for improving P&O MPPT performances of double-stage grid-connectedphotovoltaic systems,” IEEE Trans. Ind. Electron., vol. 56, no. 11, pp. 4473– 4482, Nov. 2009.
|