Keywords
|
| Mixing, period extension, pseudo random number generator (PRNG), reseeding. |
INTRODUCTION
|
| Many cryptographic applications don't have a reliable source of real random bits, such as thermal noise in electrical circuits. Instead, they use a cryptographic mechanism, called a Pseudo-Random Number Generator (PRNG) to generate these values. Pseudo random number generator (PRNG) has been widely used test pattern generation, cryptography, and telecommunication systems. But recently security applications have increased the need for strong (secure) random number generation like automatic password generation, encryption algorithms, on-line gambling etc. The PRNG collects randomness from various low-entropy input streams, and tries to generate outputs that are in practice indistinguishable from truly random streams. Typical PRNG consists of unpredictable input called “seed” value and a secret state “S”. A good PRNG should have characteristics of long-period random number sequence, a fit in statistical properties, a high throughput rate and an unpredictability. We have several Linear PRNGs, such as linear feedback shift registers (LFSRs) linear congruential generators (LCGs) , and multiple recursive generators (MRGs),which produce longperiod random number sequences. When implemented, linear PRNGs are efficient in throughput rate and hardware cost, but the output random numbers of such generators are predictable due to their linear structure. Some nonlinear PRNGs in dealt with the predictability problem, but incurred higher hardware cost and more process time. Recently, nonlinear chaos-based PRNGs (CB-PRNGs) with lower hardware cost were proposed. Chaos theory studies nonlinear systems defined on a infinite state space (e.g vectors of real numbers or infinite binary strings), whereas cryptography relies on a finite-state machine (computer). All chaos models implemented on a computer are approximations, i. e. pseudo-chaos. |
| In this we have propose a new system that consists of a CB-PRNG and a long-period MRG. The reseeding method removes the disadvantages of short periods in CB-PRNG while the mixing of the CB-PRNG with an MRG pushes the overall system period length to a value (>2 253in 32-b implementation) based on simple theoretical calculation. High throughput rate (>6.4 Gb/s) is achieved by outputting multiple bits per iteration and the hardware-efficiency is validated by using a modelsim simulator. good statistical qualities of the random numbers. |
EXISTING SYSTEM
|
| Reseeding technique is widely used in LFSR for test pattern generation Applications of LFSRs include generating pseudorandom numbers, pseudo-noise sequences, fast digital counters, and whitening sequences. and in CB-PRNG for period extension presented a reseeding method either to perturb the state value or the system parameter of digitized logistic map (LGM) for removing the short periods of a CB-PRNG. In 1998, Sang et al. applied a different reseeding method in perturbing a CB-PRNG to extend its period length up to3.3672*1029, and the lower bound of the reseeded system can be calculated. Li et al. discovered that the reseeding technique not only removes the short periods but also improves the statistical properties of CB-PRNG. |
| On the other hand, the mixing technique has been used for nonlinearity enhancement of cellular automata] and for improving statistical performance of nonlinear PRNGs. For proposed a software implementation of mixing multiple spatialtemporal CB-PRNGs to obtain high security, fast encryption (decryption) speed, and reliable robustness The mixing technique is also widely applied in period extension of nonlinear PRNGs. Gammel et al mixed several nonlinear feedback shift registers (NLFSRs) to obtain a long-period and high-throughput-rate stream cipher. In general, mixing multiple CBPRNGs results in higher hardware cost, lower throughput rate, and longer but unpredictable period length. Furthermore, one cannot be sure that the random numbers produced by these mixed PRNGs will have acceptable statistical properties. Since higher hardware cost is due to implementation of multiple CB-PRNGs which are more complex than linear PRNGs, mixing a CB-PRNG with a linear MRG instead of mixing two CB-PRNGs will reduced the hardware cost. In our proposed RM-PRNG, which consists of a CB-PRNG and an MRG, the period length is considerably extended because the period length of the MRG is much longer than that of the CB-PRNG while the short periods of the CB-PRNG can be removed by our reseeding algorithm. Note that the lower bound of the period length in RM-PRNG can be calculated analytically in terms of the period length of the CB-PRNG and that of the MRG. In addition, the throughput rate is enhanced using a vector-mixing technique in the proposed RM-PRNG. Finally, the statistical properties is improved because the linear structure of the MRGs is broken by mixing with a CB-PRNG. In Section III, we will introduce our proposed method in details. |
PROPOSED SYSTEM
|
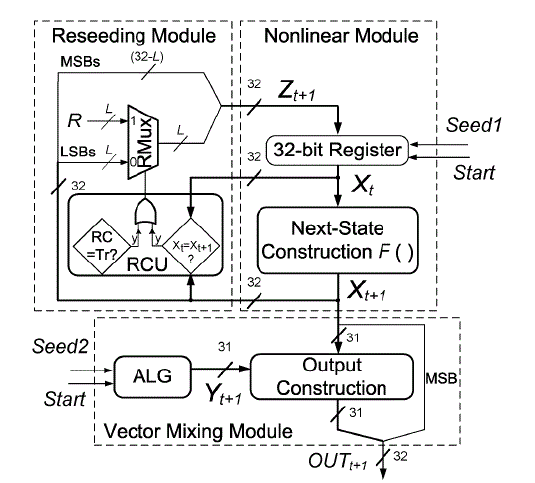
| To overcome the problems presents in the choas based design and multiple recursive generators here we proposed a new design of combination of these two systems Fig. 1 shows the diagram of the proposed system, which is composed of three modules: Nonlinear Module, Reseeding Module, and Vector Mixing Module. In implementation, the Nonlinear Module has a controlled 32-b state register and a Next-State construction circuitry. The controlled register stores the state value Xt which can be set to Seed1 by the Start command. The Next-State construction circuitry produces the next state value Xt+1 according to the recursive formula Xt+1 =F(Xt ). For each generated state value The RC will be reset and the reseeding operation will be activated when either the fixed point condition is detected or the RC reaches the reseeding period. When RC reaches the reseeding period Tr or the fixed point condition is detected then RC will be reset and the reseeding operation will be activated. The sate register will be loaded through the rmux, when reseeding is activated [1]. The value of Xt+1 is directly loaded into the state register if the reseeding is not activated. Vector Mixing Module is implemented by an auxiliary linear generator (ALG) and output construction. By mixing Xt+1 with the output Yt+1 from ALG in Vector Mixing Module, we obtain the output of the RM-PRNG (32-bit implementation).The models used in MPC are generally intended to represent the behavior of complex dynamical systems. The additional complexity of the MPC control algorithm is not generally needed to provide adequate control of simple systems, which are often controlled well by generic PID controllers. Common dynamic characteristics that are difficult for PID controllers include large time delays and high-order dynamics. |
A. Nonlinear Module
|
| The module provides an extensive set of nonlinear structural material models, including Predefined and user-defined hyperelastic materials Small-strain and large-strain plasticity models using different hardening models. We use the LGM as the next-state construction function in the Nonlinear Module so that |
 _ _ (1) _ _ (1) |
| with γ = 4 and X0 ε ( 0,1) as an initial seed. Choosing a value 4 for γ not only makes the LGM chaotic but also simplifies the implementation of to merely left-shifting the product of Xt and (1- Xt ) by 2 b. However, the state size decreases from 32 to 31 b, because the dynamics Xt and (1- Xt ) in (1) are the same. This is equivalent to a degradation of resolution by 1 b. In addition, fixed points (at Xt = 0 and 0.75) as well as short periods exist when the LGM is digitized. From exhaustive runs for all of the 232 seeds, we obtain all other periods for the 32-b LGM ( P LGM )without reseeding. They are given in Table I with the longest period (18 675) and the set of short periods Ts (≤1338) listed separately along with their total occurrences. Clearly, the performance of a CB-PRNG using only the Nonlinear Module is unsatisfactory. To solve the fixed points and short-period problem, a Reseeding Module is in order. |
B. Reseeding Module
|
| When the fixed point condition is detected or the reseeding period is reached, the value Zt+1 loaded to the state register will be perturbed away from Xt+1 in the RCU by the fixed pattern _ according to the formula given below |
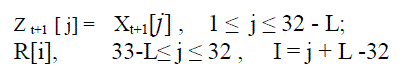 |
| where subscripts i,j are the bit-index, L is integer, and R≠0. In order to minimize the degradation of the statistical properties of chaos dynamics, the magnitude of the perturbation of the fixed pattern _ should be small compared with Xt. Here, we set L= 5 so that the maximum relative perturbation is only (2 5 – 1) /2 32. Clearly, the effectiveness of removing short-periods depends on the reseeding period T, as well as the reseeding pattern R. However, choosing the optimal reseeding period and the reseeding pattern is nontrivial. Nevertheless, several guidelines to choose a suitable combination of Tr and R had been proposed and discussed in our previous work Then no effective reseeding will be realized and the system will be trapped in the short-period cycle. Hence, prime numbers should be used as the reseeding period candidates. In this study, we use Tr and R = “18(10010)", and the result is shown in Table I. One can see that the set of short periods Ts is indeed eliminated. The lowest period, the maximum period and the average period of the reseeded PRNG are, respectively, 1929, 2 330 875, and 2 321 423.005. Although the average period of the reseeded PRNG has increased more than 100 times relative to that of the non reseeded counterpart, the period can in fact be extended tremendously in the Vector Mixing Module described below. |
C. Vector Mixing Module
|
| An efficient MRG, called the DX generator , serves as the ALG in Vector Mixing Module. Specifically, we choose the DX generator with the following recurrence equation: |
 __ _ __ (3) __ _ __ (3) |
| Using an efficient search algorithm , we find that the particular choice of Bdx = 228 + 28 and M= 231 – 1 gives the maximum period of the DX generator. The LSBs of and that of Yt+1 are mixed in the Output Construction unit using a XOR operation to obtain the least significant bits of the output according to the equation |
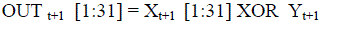 _ _ ____ (4) _ _ ____ (4) |
| Then, the most significant bit (MSB) of Xt+1 is attached to OUT t+1 [1:31] to form the full 32-b output vector OUT . |
D. DX Generator (ALG)
|
| The implementation of the DX generator is (the ALG) done by using 8-word registers, circular-left-shift (CLS), circular 3-2 counter and End Around Carry- carry look ahead adder (EAC-CLA). By using flip-flops the eight-word register was implemented. For generating two partial products signal Yt-7 is circular-left-shifted 28 and 8 b , using the modules CLS-28 and CLS-8 respectively. To combine these three 31-b operands into two 31-b operands a circular 3-2 counter is used, which consumes 247 gates. To evaluate Yt+1 31-b EAC-CLA is used with 348 gates. The schematic design of the 31-b EACCLA. The schematic design of the 31-b EAC-CLA includes four modules they are propagation and generation (PG) generators, end-around-carry (EAC) generator, internal carry (IC) generator, and CLAs. |
RESULTS AND SIMULATION
|
| Pseudo Random Number Generator, Encryption and Decryption were designed using Verilog language in ModelSim 6.3. All the simulations are performed using ModelSim 6.3 simulator. The simulated output of Pseudo Random Number Generator, Encryption and Decryption are shown in Figure 3&4. |
CONCLUSION
|
| In this paper, we proposed a cryptographic algorithm using RM-PRNG to ensure secure communication. This Cryptographic algorithm allows people to carry over the confidence found in the physical world to the electronic world, thus allowing people to do business electronically without worry of deception. With these secure communications, the proposed cryptographic algorithm using RM-PRNG can a good candidate for protect the data in ATM cards, computer passwords and electronic commerce. |
Tables at a glance
|
 |
| Table 1 |
|
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
References
|
- Chung-Yi Li, Yuan-Ho Chen, Tsin-Yuan Chang, Lih-Yuan Deng, and Kiwing To, “Period Extension and Randomness Enhancement Using High-Throughput Reseeding-Mixing PRNG”.
- J. E. Gentle, “Random Number Generation and Monte Carlo Methods”, 2nd ed. New York: Springer-Verlag, 2003.
- M. P. Kennedy, R. Rovatti, and G. Setti, “Chaotic Electronics in Telecommunications”. Boca Raton, FL: CRC, 2000.
- D. Knuth, “The Art of Computer Programming”, 2nd ed. Reading, MA: Addison-Wesley, 1981.
- A. Klapper and M. Goresky, “Feedback shift registers, 2-adic span, and combiners with memory,” J. Cryptology, vol. 10, pp. 111–147, 1997.
- D. H. Lehmer, “Mathematical methods in large-scale computing units,” in Proc. 2nd Symp. Large Scale Digital Comput. Machinery, Cambridge, MA, 1951, pp. 141–146, Harvard Univ. Press.
- S. Li, X. Mou, and Y. Cai, “Pseudo-random bit generator based on couple chaotic systems and its application in stream-ciphers cryptography,” in Progr. Cryptol.-INDOCRYPT, 2001, vol. 2247, pp. 316–329, Lecture Notes Comput. Sci.
- L. Y. Deng and H. Xu, “A system of high-dimensional, efficient, long cycle and portable uniform random number generators,” ACM Trans. Model Comput. Simul., vol. 13, no. 4, pp. 299–309, Oct. 1, 2003.
- L. Blum, M. Blum, and M. Shub, “A simple unpredictable pseudorandom number generator,” SIAM J. Comput., vol. 15, pp. 364–383, 1986.
|