International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

A Novel approach for Automatic Assessment of Objects

Dr. Aishwarya P
Professor, Dept. of CSE, Atria Institute of Technology, Bangalore, Karnataka, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

This paper proposes a new methodology of recognizing face with increased recognition rate and it‟s implemented in the field of Image Processing for Personnel verification or recognition. A major objective of this work is to develop a tool for face recognition, which can help in quicker and effective analysis of a face from the face gallery, thus reducing false acceptance rate and false rejection rate and equal error rate. Face recognition has been widely explored in the past years. A lot of techniques have been applied in various applications. Robustness and reliability have become more and more important for these applications especially in security systems. In this thesis, a variety of approaches for face recognition are reviewed first. These approaches are classified according to three basic tasks: face representation, face detection, and face identification. An implementation of the appearance-based face recognition method, the Eigen face recognition approach, is reported. This method utilizes the idea of the principal component analysis and decomposes face images into a small set of characteristic feature images called eigenfaces. This proposed work is intended to develop, multiple face Eigen subspaces. With each one is corresponding to one known subject privately, rather than all individuals sharing one universal subspace as in the traditional eigenface method. Compared with the traditional single subspace face representation, the proposed method captures the extra personal difference to the most possible extent, which is crucial to distinguish between individuals, and on the other hand, it throws away the most intrapersonal difference and noise in the input.

Keywords
Face recognition, Eigen space, subspaces, PCA

INTRODUCTION
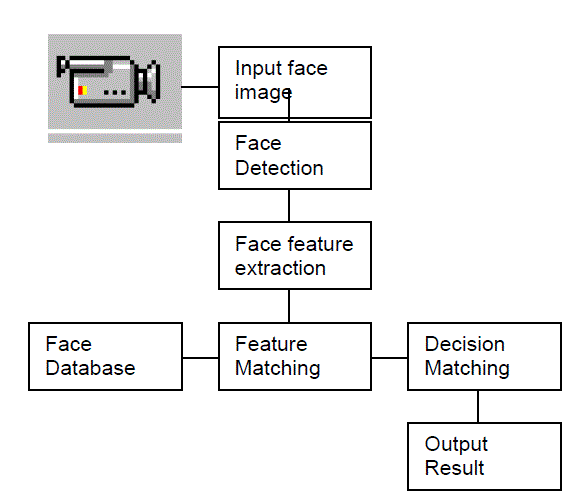
Face recognition (FR) has emerged as one of the most extensively studied research topics that spans multiple disciplines such as pattern recognition, signal processing and computer vision. This is due to its numerous important applications in identity authentication, security access control, intelligent human-computer interaction, and automatic indexing of image and video databases. Feature extraction algorithms mainly fall into two categories: geometrical features extraction and, statistical (algebraic) features extraction. The geometrical approach , represent the face in terms of structural measurements and distinctive facial features that include distances and angles between the most characteristic face components such as eyes, nose, mouth or facial templates such as nose length and width, mouth position, and chin type. These features are used to recognize an unknown face by matching it to the nearest neighbor in the stored database. Statistical features extraction is usually driven by algebraic methods such as principal component analysis (PCA), and independent component analysis (ICA). These methods find a mapping between the original feature spaces to a lower dimensional feature space.

A. Overview
The proposed method also makes use of Fuzzy Logic rules along with necessary image processing procedure. Fuzzy logic serves as a front part of the face recognition especially defined for skin area detection within the image frame. The experiments strongly supports the proposed area in which an effective performance over the traditional “eigenface” has been observed when tested on the same face base. Most of the previous work dealt with a single pose of an individual. Some common techniques included single template matching and eigenfaces. These systems were not real-time and not rotation invariant. Eigen faces described in [3] represented face images in low dimensional feature space using PCA. Initially face recognition systems focused only on single expression images. However during the previous research on face recognition system dealt with the recognition of many different views of a single image and still the recognition of the person when his expression varies is a great problem, the face recognition system is facing. Mostly in the previous researches, they use traditional Eigen value method which makes the recognition very difficult as only a single image is formed from the calculated Eigen values of a set of images. Moreover there are no implemented methods to identify the face from a real time image in the preprocessing stage when Eigen face algorithm is used as the feature extraction method. The performance of the face recognition system significantly drops when there are a large number of poses. When illumination variation is also present the task of face recognition becomes even more difficult.
Another main drawback is that it is extremely difficult to recognize the facial areas from a real time image. The traditional Eigen face method prevents us from identifying the face when a large number of expressions of the same individual is given.
The Proposed method will be trained to identify the individuals face with different expressions. As in Fig 1, The system identifies the person?s image, no matter how the expression of the face is. Individual eigenface method is to be used rather than traditional eigenvalue method. So the drawback in the traditional Eigen face method is overcome by using single eigenvalue method.
Here the calculation of eigenvalue for all the images in the database will be done and these Eigen values are compared individually with the query images eigenvalue using Euclidean distance and the results are given.
Hence the performance of the system greatly increases when the identification is done with a large number of expressions.
When a real time image is given as input, fuzzy logic is used for the identification of the facial areas from the image. This is done using the fuzzy inference system (FIS).The fuzzy logic rules are implemented in the FIS and the face areas are cropped from them. The Eigen values are then calculated for these face areas and is recognized normally.

B. Previous Works
In Eigen face, each face image is represented as a point in a low-dimensional face subspace shared by all faces; however, the experiments conducted show one of the demerits of such a strategy: it fails to accurately represent the most discriminating features of a specific face. Therefore, we propose to model each face with one individual face subspace, named Face-Specific Subspace. Distance from the face-specific subspace, that is, the reconstruction error, is then exploited as the similarity measurement for identification.

Organization of the Paper
The rest of this paper is organized as follows. An overview of Data Extraction techniques like Eigen face method is presented in Section 2. In Section 3 we explain the thresholds for face recognition. In section 4 we explain the proposed Individual eigenface subspace algorithm. Finally, Sections 5 and 6 attain the experimental results and conclusion.

DATA EXTRACTION
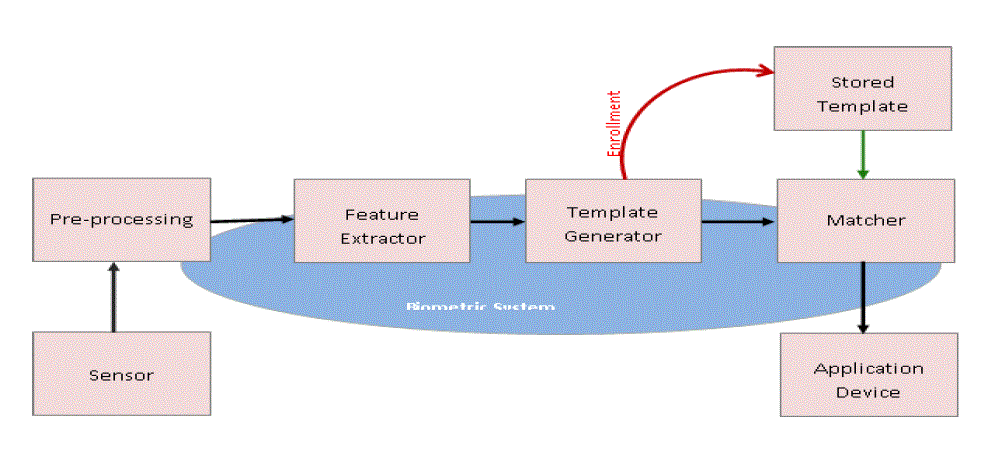
As in Fig 2, The first step in any face recognition system is the extraction of the feature matrix. A typical feature extraction algorithm tends to build a computational model through some linear or nonlinear transform of the data so that the extracted feature is as representative as possible. In this paper Eigen face method is used for feature extraction.
Eigen faces are a set of eigenvectors used in the computer vision problem of human face recognition. These eigenvectors are derived from the covariance matrix of the probability distribution of the high-dimensional vector space of possible faces of human beings. The image of the eigenface may look very little like a face.
The eigenface technique uses a strong combination of linear algebra and statistical analysis to generate a set of basis faces, the eigenfaces against which inputs are tested.
Before finding the eigenfaces, we first need to collect a set of face images. These face images become our database of known faces. We will later determine whether or not an unknown face matches any of these known faces. All face images must be the same size (in pixels. Each face image is converted into a vector Tn of length N (N=image width*image height). The most useful face sets have multiple images per person. This sharply increases accuracy, due to the increased information available on each known individual. We will call our collection of faces as face space. This space is of dimension N.
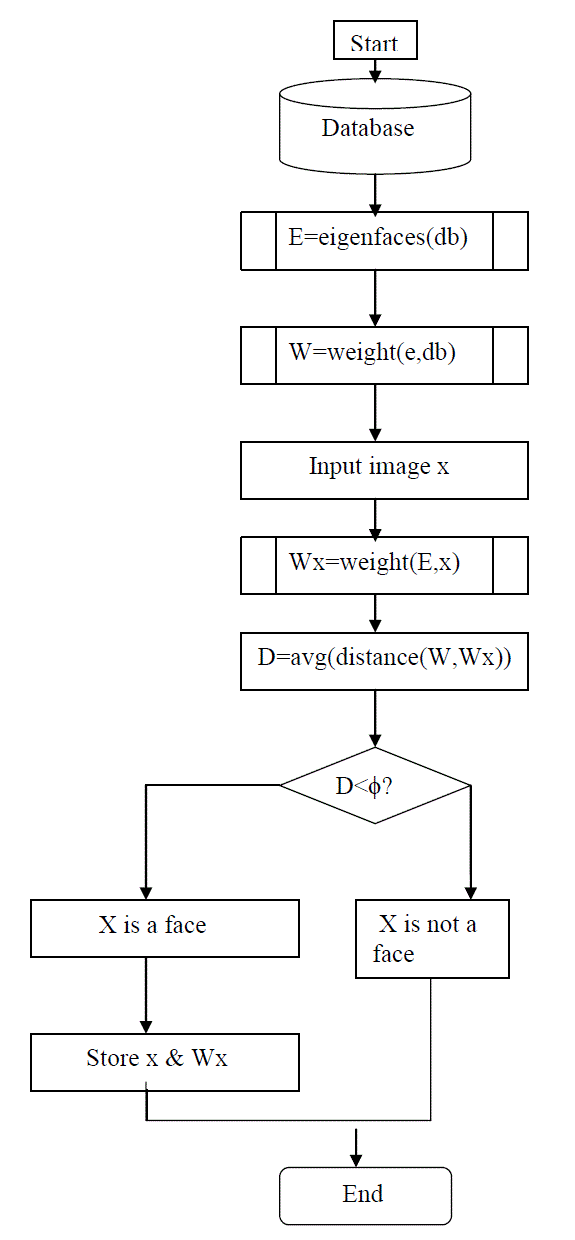
As in Fig 3, To create a set of eigenfaces, we should do the following:
1. Collect set of face images. The pictures constituting the training set should have been taken under the same lighting conditions, and must be normalized to have the eyes and mouths aligned across all images. They must also be all resample to the same pixel resolution. Each image is treated as one vector, simply by concatenating the rows of pixels in the original image, resulting in a single row with r × c elements. For this implementation, it is assumed that all images of the training set are stored in a single matrix T, where each row of the matrix contains the 'n' value of the image.
2. Calculate the average face in face space. We then compute each face difference from average. These differences are used to compute a covariance matrix(C) of our data set. The eigenfaces that we are looking for are simply the eigenvectors of C.
3. Calculate the eigenvectors and eigenvalues of the covariance matrix C. Each eigenvector has the same dimensionality (number of components) as the original images, and thus can itself be seen as an image. The eigenvectors of this covariance matrix are therefore called eigenfaces. They are the directions in which the images differ from the mean image.
4. Based on a statistical technique known as Principal Component Analysis (PCA), we can reduce the number of eigenvectors for our covariance matrix from N (the number of pixels in our image) to M (the number of images in our dataset. Choose the principal components. The eigenvectors (eigenfaces) with largest associated eigenvalue are kept.

THRESHOLD FOR EIGENFACE RECOGNITION
image
When a new image comes into the system, there are three special cases for recognition.
a) Image is a known face in the database
b) Image is a face, but of an unknown person
c) Image is not a face at all. May be a coke can, a door, or an animal
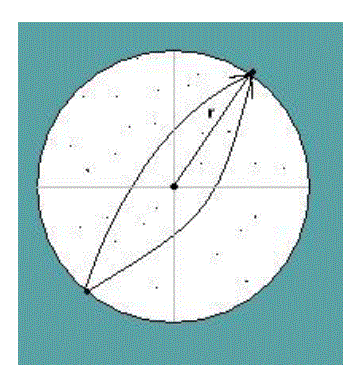
let's define the face space as an M dimensional sphere encompassing all weight vectors in the entire database. A fairly approximate radius of this face space will be half the diameter of this sphere, or mathematically, half the distance between the furthest points in the sphere.
To judge whether a new image falls within this radius, let's calculate the reconstruction error between the image and its reconstruction using M eigenfaces. If the image projects fairly well onto the face space (image follows a face distribution), then the error will be small. However a non face image will almost always lie outside the radius of the face space.
If the resulting reconstruction error is greater than the threshold, then the tested image probably is not a face image. Similar thresholds can be calculated for images of like faces. If a image passes the initial face test, it can be compared to the threshold values of faces in the database. A similar match process can be used as mentioned earlier.

INDIVIDUAL EIGENFACE SUBSPACES
Much of the previous work on eigenspace methods usually built only one eigenface space with eigenfaces of different persons, utilizing only one or very limited faces of an individual. The information of one facial image is very limited, so traditional methods have difficulty coping with differences of facial images caused by the changes of age, emotion, illumination, and hairdress. We took advantage of facial images of the same person obtained at different ages, under different conditions, and with different emotion. For every individual we constructed an eigenface subspace separately, namely multiple eigenface spaces were constructed for a face database.
We take a set of M training images and compute the eigenvectors of their covariance matrix, then select the M` eigenvectors (eigenfaces) with the highest eigenvalues to define an image subspace (face space). By projecting a faceimage into face space we obtain a „face-key? vector of M` dimensions. We define the „likenesses of any two face-images as the Euclidean distance between their respective „face-key? vectors. Using this method, we perform many comparisons between different images of the same face and images of different faces. By applying a range of threshold values to the distance measurements of these comparisons, we obtain false acceptance rates (FAR) and false rejection rates (FRR). The equal error rate (EER) is used as a single measure of the effectiveness of the system and is attained at a specific threshold value.
These may include such factors as lighting direction, intensity and color, head orientation, image quality and facial expression. For example, suppose some images in the training data were taken with bright sunlight shining on one side of the face. The feature of having one side of the face lighter than the other may be identified as a principle component and hence used to distinguish between different people.
we assume that different images of the same face map to nearby points in image space and images of different faces map to far apart points. Ideally, we wish to extract the region of image space that contains faces, reduce the dimensionality to a practical value, yet maximize the spread of different faces within the image subspace. Here we apply Principal Component Analysis to define a space with the properties mentioned above.
1. Take a set of 'M' training images
2. Compute the average image
3. find the difference of each image from average image
4. Construct the covariance matrix
5. Eigen vectors are sorted according to the Eigen values
The effect is that we have reduced the dimensionality of the space to M`, yet maintained a high level of variance between face images throughout the image subspace.
As in Fig 4, Once face space has been defined, we can project any image into face space by a simple matrix multiplication
We compare any two „face keys? by a simple Euclidean distance measure, An acceptance (the two face images match) or rejection (the two images do not match) is determined by applying a threshold. Any comparison producing a distance below the threshold is a match. To gather results for the False Rejection Rate, each of the 15 images for a single person is compared with every other image of their face. No image is compared with itself and each pair is only compared once (the relationship is symmetric), giving 6300 comparisons to test false rejection. Using these images, every person is compared with every other person. This gives 4 comparisons per pair of people, with no person compared to him and each pair only compared once. For each threshold value we produce a FAR and a FRR.

A. Rules
The rules applied for skin area discrimination are depicted below (R=Red, G=Green, B=Blue).
1. If R<100 then no skin (shadow)
2. If R<G then no skin
3. If R<B then no skin
4. If R/G >1.3 and R/B >1.4 then possible skin
5. If R/G <1.3 or R/B <1.4 then no skin
6. If R/G >1.3 and G/B >1.5 then possible skin
7. If R/G <1.3 or R/B <1.4 then no skin
8. If 77<G<127 and 133<B<173 then possible skin

RESULTS OF EIGENFACE DETECTION TESTS
The best average recognition rate of 94.8% is achieved using Multiple face Eigen subspace technique. In this instance, the selection algorithm reduces the size of the original feature vector by nearly 50%. In general the performance in terms of recognition rates are same with general eigenface technique but the number of selected features is smaller when using the multiple face Eigen subspace algorithm. In terms of computational time, this method takes less training time than the generalized algorithm in all tested instances.

CONCLUSION & FUTURE WORK
Analysis of the eigenface recognition technique using Individual face eigenspace method gives evidence that the methods prove, at best, 90% accurate. This indicates that in any implementation of such recognition system there does not exist a meaningful advantage to using more eigenfaces than first provide the desired level of accuracy.
In this way it becomes evident that if higher success rates are to be assured in most reasonable conditions then refinements to the eigenface concept must be made. Clearly the eigenface algorithm much promise for the field of facial image recognition but not before some technical refinement.
The future work may involve the implementation of fuzzy logic in such a way that the recognition has a fast operation .The input real image can be preprocessed still more efficiently so that even the very small images can also be identified and recognized. The recognition can also applied to image sequences rather than still images.
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
Figure 5 Figure 6 Figure 7
Figure 5 Figure 6 Figure 7
 

References