A Novel Approach for Generating Test Patterns Using ALU

Abstract

The increase of the Integrated Circuit (IC) capabilities offers the designer the possibility to include more complex functionality into it. Processors are one of the general purpose modules found in these complex circuits which can be reused for test. It has been shown that processors can reach similar levels of Fault Coverage (FC) to LFSR, by looping arithmetic operations. Weighted pseudorandom techniques have also been used to improve the fault coverage. These weighted pseudorandom techniques result in low testing time and power. Generation of test vectors using arithmetic functions is becoming an attractive solution due to possibility of reusing internal arithmetic data paths of system cores for testing purposes. It requires neither additional IC area nor special bus to transmit test vectors; these can be sent by standard address or data buses to the Modules Under Test (MUT). Of the four basic arithmetic operations that are available in processors, addition has the most advantages: it is usually implemented by hardware, and it is more energy and time efficient. Also, if the buses require the The increase of the Integrated Circuit (IC) capabilities offers the designer the possibility to include more complex functionality into it. Processors are one of the general purpose modules found in these complex circuits which can be reused for test. It has been shown that processors can reach similar levels of Fault Coverage (FC) to LFSR, by looping arithmetic operations. Weighted pseudorandom techniques have also been used to improve the fault coverage. These weighted pseudorandom techniques result in low testing time and power. Generation of test vectors using arithmetic functions is becoming an attractive solution due to possibility of reusing internal arithmetic data paths of system cores for testing purposes. It requires neither additional IC area nor special bus to transmit test vectors; these can be sent by standard address or data buses to the Modules Under Test (MUT). Of the four basic arithmetic operations that are available in processors, addition has the most advantages: it is usually implemented by hardware, and it is more energy and time efficient. Also, if the buses require thetransmission of the test vector by pieces, it can be split into smaller operations by propagating the carry signal. This project proposes a method for designing a low power and area efficient test pattern generator (TPG) using ALU. The TPG is designed using a newly proposed Carry Select Adder in place of the binary adders in ALU. This helps to achieve low power consumption , low area and less speed too than the earlier designs.

Keywords

TPG, MUT, LFSR, Newly Proposed Carry Select Adder.

INTRODUCTION

Pseudorandom built-in self test (BIST) generators have been widely utilized to test integrated circuits and systems. The arsenal of pseudorandom generators includes, among others, linear feedback shift registers (LFSRs), cellular automata [2], and accumulators driven by a constant value . For circuits with hard-to-detect faults, a large number of random patterns have to be generated before high fault coverage is achieved. Therefore, weighted pseudorandom techniques have been proposed where inputs are biased by changing the probability of a “0” or a “1” on a given input from 0.5 (for pure pseudorandom tests) to some other value .

Weighted random pattern generation methods relying on a single weight assignment usually fail to achieve complete fault coverage using a reasonable number of test patterns since, although the weights are computed to be suitable for most faults, some faults may require long test sequences to be detected with these weight assignments if they do not match their activation and propagation requirements. Multiple weight assignments have been suggested for the case that different faults require different biases of the input combinations applied to the circuit, to ensure that a relatively small number of patterns can detect all faults. Approaches to derive weight assignments for given deterministic tests are attractive since they have the potential to allow complete coverage with a significantly smaller number of test patterns.

In order to minimize the hardware implementation cost, other schemes based on multiple weight assignments utilized weights 0, 1,and 0.5. This approach boils down to keeping some outputs of the generator steady (to either 0 or 1) and letting the remaining outputs change values (pseudo-) randomly (weight 0.5). This approach, apart from reducing the hardware overhead has beneficial effect on the consumed power, since some of the circuit under test (CUT) inputs (those having weight 0 or 1) remain steady during the specific test session.

Current VLSI circuits, e.g., data path architectures, or digital signal processing chips commonly contain arithmetic modules [accumulators or arithmetic logic units (ALUs)]. This has fired the idea of arithmetic BIST (ABIST) . The basic idea of ABIST is to utilize accumulators for built-in testing (compression of the CUT responses, or generation of test patterns) and has been shown to result in low hardware overhead and low impact on the circuit normal operating speed. Manich et al. presented an accumulator-based test pattern generation scheme that compares favorably to previously proposed schemes.It was proved that the test vectors generated by an accumulator whose inputs are driven by a constant pattern can have acceptable pseudorandom characteristics, if the input pattern is properly selected.However, modules containing hard-todetect faults still require extra test hardware either by inserting test points into the mission logic or by storing additional deterministic test patterns .

In order to overcome this problem, an accumulator-based weighted pattern generation scheme was proposed. The scheme generates test patterns having one of three weights, namely 0, 1, and 0.5 therefore it can be utilized to drastically reduce the test application time in accumulator-based test pattern generation. However, the scheme proposed possesses three major drawbacks: 1) it can be utilized only in the case that the adder of the accumulator is a ripple carry adder; 2) it requires redesigning the accumulator; this modification, apart from being costly, requires redesign of the core of the datapath, a practice that is generally discouraged in current BIST schemes; and 3) it increases delay, since it affects the normal operating speed of the adder.In the base paper a novel scheme for the weighted pattern generation which does not impose any condition on the adders used was studied.

In this paper a novel scheme for the design of low power and area efficient test pattern generator using ALU is proposed. This paper is organized as follows. In Section II, the idea underlying the accumulator-based 3- weight generation is presented. In Section III, the design methodology to generate the 3-weight patterns utilizing an accumulator is presented. In section IV the results have been compared.

ACCUMULATOR-BASED 3-WEIGHT PATTERN GENERATION

We shall illustrate the idea of an accumulatorbased 3-weight pattern generation by means of an example. Let us consider the test set for the c17 ISCAS benchmark [12], [31] given in Table I. Starting from this deterministic test set, in order to apply the 3-weight pattern generation scheme, one of the schemes proposed in [5], [8], and [9] can be utilized. According to these schemes, a typical weight assignment procedure would involve separating the test set into two subsets, S1 and S2 as follows: S1={T1, T4},S2 ={T2 ,T3}.

The weight assignments for these subsets is W{S1} ={_,_,1,_,1} and W{S2} = {_,_,0,1,0} , where a “_” denotes a weight assignment of 0.5, a “1” indicates that the input is constantly driven by the logic “1” value, and “0” indicates that the input is driven by the logic “0” value. In the first assignment, inputs A[2] and A[0] are constantly driven by “1”, while inputs A[4], A[3], A[1] are pseudo randomly generated (i.e., have weights 0.5). Similarly, in the second weight assignment (subset S2), inputs A[2] and A[0] are constantly driven by “0”, input A[1] is driven by “1” and inputs A[4] and A[3] are pseudo randomly generated.

The above reasoning calls for a configuration of the accumulator, where the following conditions are met: 1) an accumulator output can be constantly driven by “1” or “0” and 2) an accumulator cell with its output constantly driven to “1” or “0” allows the carry input of the stage to transfer to its carry output unchanged. This latter condition is required in order to effectively generate pseudorandom patterns in the accumulator outputs whose weight assignment is “_”.

DESIGN METHODOLOGY

The implementation of the weighted-pattern generation scheme is based on the full adder truth table, presented in Table II. From Table II we can see that in lines #2, #3, #6, and #7 of the truth table,Cout=Cin. Therefore, in order to transfer the carry input to the carry output, it is enough to set A[i] = not B[i]. The proposed scheme is based on this observation.

The implementation of the proposed weighted pattern generation scheme is based on the accumulator cell presented in Fig. 1, which consists of a Full Adder (FA) cell and a D-type flip-flop with asynchronous set and reset inputs whose output is also driven to one of the full adder inputs. In Fig. 1, we assume, without loss of generality, that the set and reset are active high signals. In the same figure the respective cell of the driving register B[i] is also shown. For this accumulator cell, one out of three configurations can be utilized, as shown in Fig. 2.

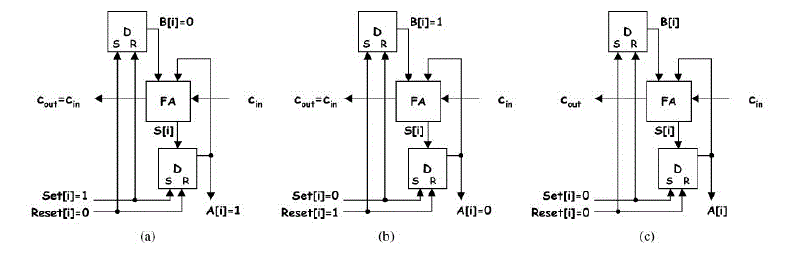
In Fig. 2(a) we present the configuration that drives the CUT inputs when A[i]=1 is required.Set[i]=1 and Reset[i] = 0 and hence A[i]=1 and B[i] =0. Then the output is equal to 1, and Cin is transferred to Cout.

In Fig. 2(b), we present the configuration that drives the CUT inputs when A[i]=0 is required. Set[i]=0 and Reset[i] = 1 and hence A[i]=0 and B[i]=1. Then, the output is equal to 0 and Cin is transferred to Cout.

In Fig. 2(c), we present the configuration that drives the CUT inputs when A[i]= _ is required. Set[i]=0 and Reset[i] = 0.The D input of the flip-flop of register B is driven by either 1 or 0, depending on the value that will be added to the accumulator inputs in order to generate satisfactorily random patterns to the inputs of the CUT.

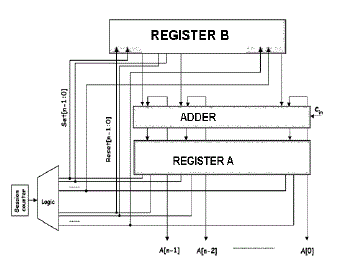
In Fig. 3, the general configuration of the proposed scheme is presented.The Logic module provides the Set[n-1:0] and Reset[n-1:0] signals that drive the S and R inputs of the Register A and Register B inputs. Note that the signals that drive the S inputs of the flip-flops of Register A, also drive the R inputs of the flip-flops of Register B and vice versa. In the figure 2 , the performance of the circuit is increased by using a modified carry select adder as follows.

MODIFIED CSLA USING BEC

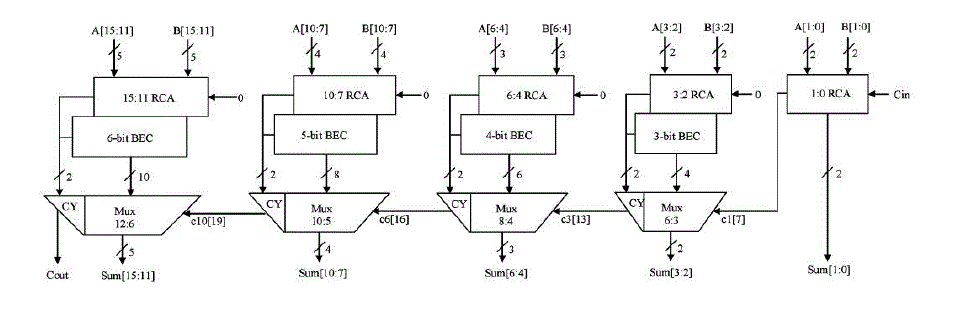
The Binary to excess one Converter (BEC) replaces the ripple carry adder with Cin=1, in order to reduce the area and power consumption of the regular CSLA. The modified16-bit CSLA using BEC is shown in Fig. 4 [1]. The structure is again divided into five groups with different bit size RCA and BEC.The group 2 of the modified 16-bit CSLA is shown Fig. 5. By manually counting the number of gates used for group 2 is 43 (full adder, half adder, multiplexer, BEC).One input to the mux goes from the RCA with Cin=0 and other input from the BEC. Comparing the group 2 of both regular and modified CSLA, it is clear that BEC structure reduces the area and power. But the disadvantage of BEC method is that the delay is increasing than the regular CSLA [8].

PROPOSED CSLA ARCHITECTURE

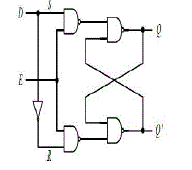
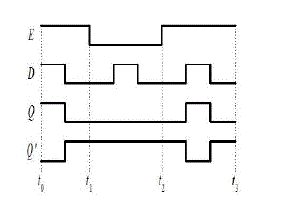
This method replaces the BEC add one circuit by Dlatch with enable signal. Latches are used to store one bit information. Their outputs are constantly affected by their inputs as long as the enable signal is asserted. In other words, when they are enabled, their content changes immediately according to their inputs. D-latch and it’s waveforms are shown in Fig. 6 and Fig. 7 respectively [7].

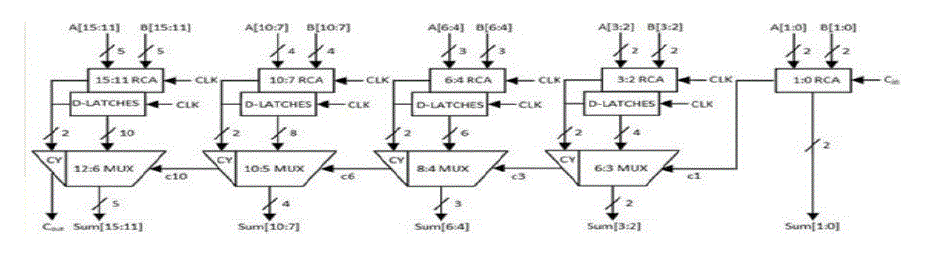
The architecture of proposed 16-b CSLA is shown in Fig. 8. It has different five groups of different bit size RCA and D-Latch. Instead of using two separate adders in the regular CSLA, in this method only one adder is used to reduce the area, power consumption and delay. Each of the two additions is performed in one clock cycle.

This is 16-bit adder in which least significant bit (LSB) adder is ripple carry adder, which is 2 bit wide. The upper half of the adder i.e, most significant part is 14-bit wide which works according to the clock. Whenever clock goes high addition for carry input one is performed. When clock goes low then carry input is assumed as zero and sum is stored in adder itself. From the Fig. 9, it can understand that latch is used to store the sum and carry for Cin=1.

Carry out from the previous stage i.e, least significant bit adder is used as control signal for multiplexer to select final output carry and sum of the 16-bit adder. If the actual carry input is one, then computed sum and carry latch is accessed and for carry input zero MSB adder is accessed. Cout is the output carry.

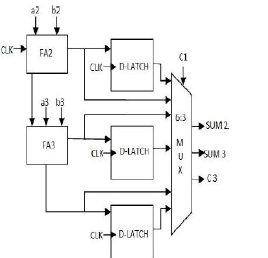
The Fig.7 shows the internal structure of group 2 of the proposed 16-bit CSLA. The group 2 performed the two bit addition which are a2 with b2 and a3 with b3. This is done by two full adder (FA) named FA2 and FA3 respectively. The third input to the full adder FA2 is the clock instead of the carry and the third input to the full adder FA3 is the carry output from FA2. The group 2 structure has three D-Latches in which two are used for store the sum2 and sum3 from FA2 and FA3 respectively and the last one is used to store carry. Multiplexer is used for selecting the actual sum and carry according to the carry is coming from the previous stage. The 6:3 multiplexer is the combination of 2:1 multiplexer.

When the clock is low a2 and b2 are added with carry is equal to zero. Because of low clock, the D-Latch is not enabled. When the clock is high, the addition is performed with carry is equal to one. All the D-Latches are enabled and store the sum and carry for carry is equal to one. According to the value of c1 whether it is 0 or 1, the multiplexer selected the actual sum and carry.

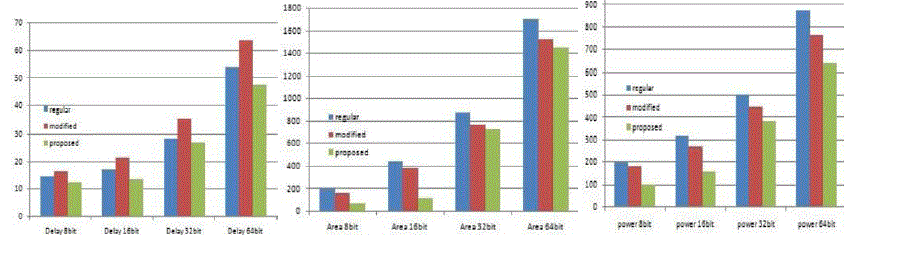
Fig. 9, 10 and 11 depicts that the newly proposed adder consumes less area ,power and delay than the modified CSLA.

CONCLUSION

A regular CSLA uses two copies of the carry evaluation blocks, one with block carry input is zero and other one with block carry input is one. Regular CSLA suffers from the disadvantage of occupying more chip area. The modified CSLA reduces the area and power when compared to regular CSLA with increase in delay by the use of Binary to Excess-1 converter. This paper proposes a scheme which reduces the delay, area and power than regular and modified CSLA by the use of D-latches. Thus the ALU based test pattern generator using this newly proposed carry select adder also consumes less delay, area and power.

Tables at a glance

Table 1 Table 2

Figures at a glance

Figure 1 Figure 2 Figure 3 Figure 4 Figure 5 Figure 6 Figure 7 Figure 8

References

Antonis Paschalis, IoannisVoyiatzis, and DimitrisGizopoulos ,”Accumulator based 3 weight pattern generation,” IEEE Trans.Very Large Scale Integr. (VLSI) Syst., vol. 20, no. 2, pp. 357–361,Feb. 2012. E. Kalligeros, X. Kavousianos, D. Bakalis, and D. Nikolos, “Anefficient seeds selection method FOR LFSR-based test-per-clockBIST,” in Proc. Int. Symp. Quality Electron. Des. , 2002, p. 261. A. Stroele, “A self test approach using accumulators as test pattern generators,” in Proc. Int. Symp. Circuits Syst., 1995, pp.2120–2123. P. Hortensius, R. McLeod, W. Pries, M. Miller, and H. Card, “Cellular automata-based pseudorandom generators for built-inself test,” IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst., vol. 8, no. 8, pp. 842–859, Aug. 1989. S. Wang, “Low hardware overhead scan based 3-weight weighted random BIST,” in Proc. IEEE Int. Test Conf., 2001, pp. 868–877. Voyiatzis, D. Gizopoulos, and A. Paschalis, “Accumulator-based weighted pattern generation,” presented at the IEEE Int. Line Test Symp., Saint Raphael, French Riviera, France, Jul. 2005. H.J. Wunderlich, “Self test using unequiprobable random patterns,” in Proc. 17th Int. Symp. Fault-Tolerant Comput.(FTCS), 1987, pp.258–263. B. Ramkumar and Harish M Kittur.” Low-Power and Area- Efficient Carry Select Adder,” IEEE Trans. Very Large ScaleIntegr. (VLSI) Syst., vol. 20, no. 2, pp. 371–375, Feb. 2012.