ISSN: 2319-9873
ISSN: 2319-9873
Moses E Emetere1*, Uno E Uno2 and KU Isah2
1Department of Physics, Covenant University Canaanland P.M.B 1023, Otta, Nigeria.
2Department of Physics, Federal University of Technology, Minna, Nigeria.
Received: 13/01/2014; Revised: 22/02/2014; Accepted: 25/02/2014
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
The introduction of velocity ratios (of electrons within the superconducting system) as one of superconducting parameters has been earlier established. Further investigation on the effects of velocity ratio to complex systems was examined at different relaxations. The model clarified the conditions for both positive and negative relaxation of current in complex bodies e.g. superconductor, spintronics e.t.c. The relaxation rates discovered to proportional to the velocity ratios.
stretched-exponential decay, superconductivity, velocity ratios, Bloch NMR
The stretched-exponential decay law has been used in complex condensed matter systems, though it has been confirmed in several other materials like polymer, [1] fluorescence in porous glass, [2] porous silicon, [3] InGaN light-emitting diodes, [4] poly films, [5] crystalline solids, [6] organic scintillators, [7]. Nevertheless, none of these features noticed in the fore mentioned materials have shown a perfect understanding of the relaxation phenomenon in complex systems e.g. superconductors.
Initially, the application of stretched-exponential decay in systems was attributed to the role of disorder in materials [3] and the recombination of localized excitons in an undulating quantum wires or dots [2]. The ab-initio objective of the stretched exponential decay law in condensed matter systems was to analyze dispersive diffusion of the photoexcited carriers which may be due to excitation of carriers from localized to extended states or to hopping between localized states [3], distribution of the crystalline size and shape, fluctuations of the surface structure and stoichiometry [8], and Monte-Carlo simulations of chain configuration and dynamics of condensed matter systems [9,10]. All these attributes of the stretched – exponential decay have not answered the questions on some strange events like the reduction of critical current and trapped magnetic moment with time in the field of condensed matter physics.
From the most general idea of superconductivity, electron –phonon interactions is the signature of the classical low-Tc superconductors [11] while the theory of the high-Tc superconductors is opposed to the low-Tc superconductors [12]. This idea makes the computation of the stretched exponential decay law none effect for this type of complex systems. The lattice dynamics of superconductors are strongly influenced by doping [13] of the superconductor. One of the effects of doping is the formation of surface or stoichiometry disorders in materials. This idea is the basis for the introduction of stretched –exponential decay to explain relaxation in complex materials in this paper.
Generally, the concept of magnetic relaxation centers on magnetic moment changing logarithmically with time. The magnetic relaxation of low temperature superconductors were first examined by Anderson [14], though much interest was not shown by researchers due to its small effects. The high temperature superconductors on the other hand showed prospects. First, the Anderson – Kim model showed that the functional form of the time relaxation was approximately logarithmic. [14] It was later disputed by Thompson et al [15] that the functional form of the time relaxation was semi-logarithmic. Several experimental and theoretical studies have been carried-out but a concrete agreement on the functional form of the time relaxations in complex materials e.g. superconductors have not been established.
Recently we have worked on superconducting features where mathematical derivations were made to totally investigate the magnetic penetration depth with emphasis on the fundamentals of the magnetic relaxation i.e. the mixed phase given by Abrikosov [16]. The research entailed the use of Bloch NMR equations to analyze the penetrating depth of superconducting materials. The velocity ratios of interacting electrons were derived which was believed to be a vital parameter for superconductivity. In this paper, further analysis was carried out on the velocity ratios of interacting electrons during magnetic relaxation. The solutions from the dynamic Kubo-Toyabe function for spin polarization [17] were incorporated into the remodeled stretched-exponential decay to accurately investigate the significance of the dynamics of interacting electrons.
The Bloch NMR solutions of the Muon- spin relaxation rate carried out by Uno et al. [17] showed the relationship between the velocity ratio with the relaxation as shown below
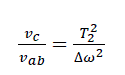 (1)
(1)
Or
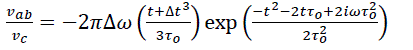 (2)
(2)
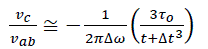 (3)
(3)
Ab-initio, the stretched exponential decay law is written as follows
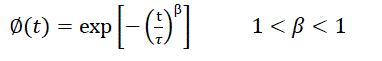 (4)
(4)
Comparing equation [2] & [4], there are similarities noticed - when the system fluctuates out of equilibrium, it returns by the function 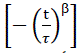 (6) also, in the superconducting system, the fluctuated system returns back to equilibrium by the function
(6) also, in the superconducting system, the fluctuated system returns back to equilibrium by the function 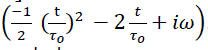 . In the remodeled stretched exponential decay law for superconducting systems, we propounded
. In the remodeled stretched exponential decay law for superconducting systems, we propounded
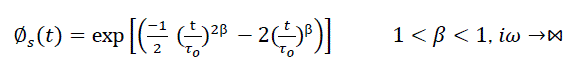 (5)
(5)
It is therefore expected that the distribution of decay times or rate constant (shown in equation [50] ) would account for the observed phenomenon in a complex system. Before now, there had been theoretical arguments on the magnitude of the -factor. For example, Rice et al. [18] noticed that in the original stretched exponential decay, diffusion-controlled contact luminescence quenching occurs when 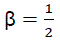 . Förster et al. [19] reported that diffusionless resonance energy transfer by the dipole–dipole mechanism occurs when
. Förster et al. [19] reported that diffusionless resonance energy transfer by the dipole–dipole mechanism occurs when 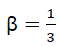 and
and 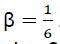 . For the proper analysis of the remodeled stretch exponential decay for a more complex systems, the following β- factors would be used i.e.
. For the proper analysis of the remodeled stretch exponential decay for a more complex systems, the following β- factors would be used i.e. 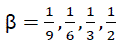
First we shall compare the result of the remodeled law ( i.e. equation [5]) with the erstwhile law(i.e. equation [4]) as shown in the figure [1-4] below
Since the β– factors has its individual effects on the normal stretched exponential decay, the behavior of equation [5] was tested under various β– factors (majorly 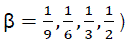 . Two cases were considered i.e. τ > t and τ < t as shown in figure [5&6]
. Two cases were considered i.e. τ > t and τ < t as shown in figure [5&6]
Since the velocity ratio is a new concept we are incorporating into the complex bodies [14], we modeled it into stretch exponential decay [6].
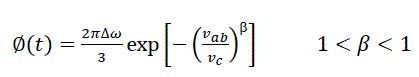 (6)
(6)
The frequency is given as Δω = 200MHz. The velocity ratio is investigated to see its reactions at different conditions (as shown in figure [7 & 8] ) e.g. for holistic analyses, the applied β– factors are 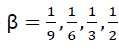
The relationship between the velocity ratios and the relaxation time were worked out as shown in equation [7] below. Unlike the Anderson-Kim theory which deals with measurement of the normalized relaxation rate to determine the pinning barrier, equation [7] measures the normalized relaxation rate to determine the effects of velocity ratio on particulate dynamics of a complex system.
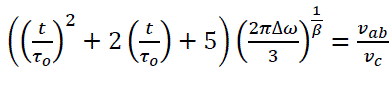 (7)
(7)
It is known that the current relaxation rate exponentially decreases if the relaxing superconductor is cooled to ΔT [20]. It was mathematically expressed as
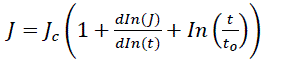 (8)
(8)
Krables et al., [21] reported that when the temperature is lowered from 78K to 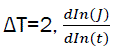 reduces by 6 times and
reduces by 6 times and 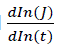 reduces by 200 times when the temperature is decreased to ΔT = 4K. The anomaly noticed by the changing logarithmic relaxation rate
reduces by 200 times when the temperature is decreased to ΔT = 4K. The anomaly noticed by the changing logarithmic relaxation rate 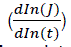 is related to the trapped magnetic moment within the superconducting tablet or annuli which have been found to be caused by magnetic flux creep [22]. Relating the velocity ratio of electrons to the causes of magnetic flux creep is the objective of this section. Equation [7] was incorporated into equation [8] with an assumption from an earlier work on NMR modeling [23]
is related to the trapped magnetic moment within the superconducting tablet or annuli which have been found to be caused by magnetic flux creep [22]. Relating the velocity ratio of electrons to the causes of magnetic flux creep is the objective of this section. Equation [7] was incorporated into equation [8] with an assumption from an earlier work on NMR modeling [23] 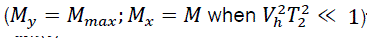 to substitute for the value of Δω engendered
to substitute for the value of Δω engendered
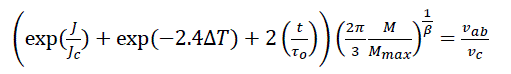 (9)
(9)
Equation [9], therefore incorporates all the parameters which is explained graphically in Figure(10). The magnetization ratio was considered for two striking point of an experimental work [24] 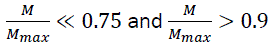
The mathematical expression for the luminescence decay of normal and superconducting material (as shown in figure [1]) can be related mathematically as 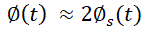 when decay sets in. When the decay draws close to fizzling out (as shown in figure [2]), the luminescence decay for both material initially possess a mathematical relation
when decay sets in. When the decay draws close to fizzling out (as shown in figure [2]), the luminescence decay for both material initially possess a mathematical relation 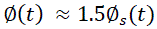 and later coincide at a particular relaxation rate. At high relaxation rate, equation [4] decays while equation [5] still exhibit its parabolic nature (as shown in Fig.[3&4]). This property confirms the characteristics of the families of high- temperature superconductors; hence it is valid to describe other concept of complex body systems.
and later coincide at a particular relaxation rate. At high relaxation rate, equation [4] decays while equation [5] still exhibit its parabolic nature (as shown in Fig.[3&4]). This property confirms the characteristics of the families of high- temperature superconductors; hence it is valid to describe other concept of complex body systems.
Testing the β– factors to see its characteristic nature in a superconductivity system(Fig.[5&6]), it was observed that diffusion-controlled contact luminescence quenching also occurs in superconducting system at 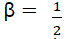 this confirms the idea of Förster et al. (19). The only varying idea of this paper to Förster et al is that luminescence quenching is pronounce at high relaxation rates and fizzles out at lower relaxation rates. The relaxation behavior was proven (Fig.[7&8] to be dependent on the velocity ratios of the electrons which forms various current paths within different regions of the superconducting layers. Further proof of the velocity ratio connection to relaxation rates was shown in Fig.[9] and equation[6]. This is interpreted that as relaxation occurs within a superconducting system, the velocity ratio explains the possibility of obtaining both negative and positive relaxation of current within regions of the superconducting layers. Figure [10] showed that when logarithmic relaxation rate
this confirms the idea of Förster et al. (19). The only varying idea of this paper to Förster et al is that luminescence quenching is pronounce at high relaxation rates and fizzles out at lower relaxation rates. The relaxation behavior was proven (Fig.[7&8] to be dependent on the velocity ratios of the electrons which forms various current paths within different regions of the superconducting layers. Further proof of the velocity ratio connection to relaxation rates was shown in Fig.[9] and equation[6]. This is interpreted that as relaxation occurs within a superconducting system, the velocity ratio explains the possibility of obtaining both negative and positive relaxation of current within regions of the superconducting layers. Figure [10] showed that when logarithmic relaxation rate 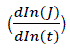 maintains its features i.e.
maintains its features i.e. 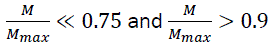 , the velocity ratio
, the velocity ratio 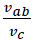 decreases and increases respectively. This means that increased velocity ratio
decreases and increases respectively. This means that increased velocity ratio 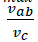 supports the positive relaxation while a decreased velocity ratio supports the negative relaxation in complex body systems.
supports the positive relaxation while a decreased velocity ratio supports the negative relaxation in complex body systems.
In conclusion, the velocity ratio within the regions of the superconducting system strongly affects the current relaxation in the superconductor-thereby validating the remodeled exponential decay law for complex body system. Since the equation [9] shows two different characteristics at different relaxation rates, this may account for the currents near the outer surface of the superconductor to diminish slower than the internal currents, which vary in the opposite direction. The luminescence decay of complex systems has a changing phase within specific relaxation rates.
This work is self-funded. We appreciate Mrs. Jennifer Emetere for editing the script.