International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

A Review on Combined Economic and Emission Dispatch using Evolutionary Methods

Dimple Singla1, Sanjay K. Jain2
  1. PG Student [PSED], Dept. of EIED, Thapar University, Patiala, Punjab, India
  2. Associate professor, Dept. of EIED, Thapar University, Patiala, Punjab, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Economic load dispatch is an important optimization problem in power system. Due to the harmful effects of the emission released by fossil fueled electric power plants, Emission Dispatch plays an important role in power industry. This leads to the formulation of combined economic and emission dispatch (CEED) problem. This paper presents a review on evolutionary methods for solving combined economic and emission dispatch problems which mainly include Genetic Algorithm based approach, Particle Swarm Optimization (PSO), Differential Evolution (DE),Strength Pareto Evolutionary Algorithm (SPEA), Artificial Immune System (AIS) which will encourage the researches for providing better solution for CEED optimization in power system.

Keywords
Combined economic and emission dispatch (CEED), Evolutionary algorithm, GA, PSO, DE, SPEA, AIS.

INTRODUCTION
The aim of power industry is to generate electrical energy at minimum cost while satisfying all the limits and constraints imposed on generating units. Economic Load dispatch (ELD) is the one of the optimization problem in power industry. ELD determines the optimal power solution to have minimum generation cost while meeting the load demand. But due to environment issues which are arising from the emissions produced by the fossil fuels in thermal power plant, it has become mandatory for power utility to consider the environment constraints along with the economy. But both of the objectives i.e. minimum fuel cost and minimum emission are of conflicting nature. This problem leads to the formulation of multiobjective economic load dispatch. Or it can also be formulated as combined economic and emission dispatch (CEED) problem.
In fossil-fired power plants, main sources of energy are coal, gas, oil and diesel. All of the above mentioned resources realize harmful gases in atmosphere. Coal Produces ash content, SOx, NOx, and CO2 in the atmosphere. The cooling water used in thermal power plant also rises the water temperature and affecting the marine life also. Nuclear power plants emit harmful radiation in the environment. Because of all above factors, emission control has become an important operational objective.
Conventionally classical optimization technique such as Langarangian Relaxation [1], Gradient and Dynamic programming method[2-3], Integer programming[4], Lambda-iteration [5], Newton Raphson Method[6] were used for economic load dispatch problem. These methods need derivative information of the objective function [7], give non satisfactory results and require large computational time for non-linear complex problems. Linear programming method [8] suffers from the limitation as it require piecewise linear cost approximation. Newton based methods struggle with handling a large number of inequality constraints [9]. Recently various heuristic search techniques such as Particle Swarm Optimization (PSO) [10], Genetic Algorithm (GA) [11], Differential Evolution (DE) [12], Ant Colony Search Method [13], Evolutionary Programming [14], and Artificial Bee Colony (ABC) method [15] have been used to solve complex optimization problem.
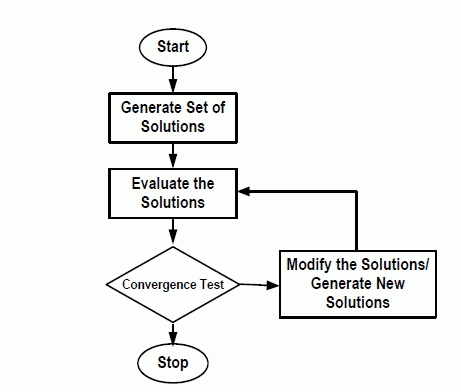
An evolutionary algorithm is an evolutionary computation, a generic population based metaheuristic optimization algorithm. The Fig. 1 represents the iterative computational process of evolutionary algorithm. This paper presents a summary of evolutionary algorithms which mainly include Genetic Algorithm based approaches, Particle Swarm optimization (PSO), Differential Evolution (DE), Strength Pareto Evolutionary Algorithm (SPEA), Artificial Immune System (AIS) for environmental-economic dispatch in power system.
In electric power system, there are mainly four objectives to be minimized which include the economy and environmental impacts because of NOx, SO2 and CO2 gaseous pollution.
A. Economic Dispatch:
In thermal power plants, fuel cost is an important criterion for economic feasibility. The economic dispatch problem can be formulated by using quadratic or cubic functions of generated power. But in literature review, most of the papers consider only second order polynomial function for economic dispatch problem formulation. The objective function can be described as:
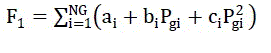image (1)
Where F1 is the total operating fuel cost in Rs. /hr. Pgi is the decision variable, i.e. real power generation corresponding to the ith generating unit .NG is the number of generating units and ai , bi , ci are the cost coefficients of the ith generating unit.
Subjected to:
1. Equality Constraint:
The total real power generation must be able to meet total system demand and total system losses i.e.
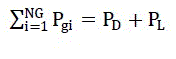image(2)
PDrepresents the total load demand and PL represents the total transmission loss.
2. Inequality constraint/Limits on variables:
The power output of each generator must be within maximum and minimum generating limits i.e.
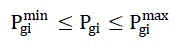image(3)
Pgi min and Pgi max are the minimum and maximum power output of the ith generating unit respectively.
B. Emission Dispatch:
The main objective of the emission dispatch is to maintain the pollution within environment license irrespective of the fuel type. The minimum emission dispatch problem can be formulated as follows: The objective function can be described as:
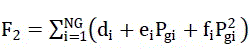image(4)
Where di , eiand fi are emission coefficients of the ith unit and F2 is the total emission level in ton/hr.
C. Total Objective Function:
Aggregating equations (1) to (4), multi-objective problem can be formulated as:
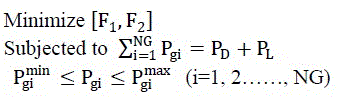image(5)
Where F1 and F2 are the objective functions to be minimized.
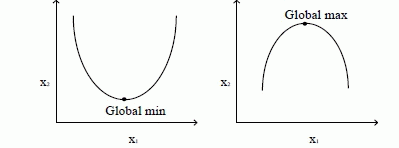
In single objective optimization problem, there exists only one optimal solution, if the problem is convex for a minimizing problem or concave for a maximizing objective function as shown in fig. 2.
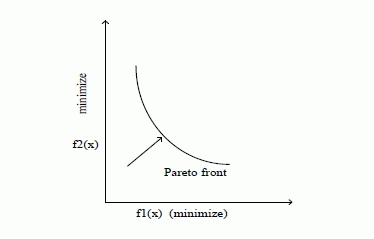
Although, most of research considers a single objective optimization problem, many real world problems are multiobjective by nature. Due to presence of conflicting objective, a single solution to all objectives does not exist. An effort is made to find a set of trade-off optimal solutions, called Pareto-optimal solution. The set of all feasible non-dominated solutions is called Pareto-optimal set. And for a given Pareto optimal set, the corresponding objective function values in the objective space is called the Pareto optimal front. Fig. 3 represents the Pareto optimal front for min-min type optimization problem.

GENETIC ALGORITHM (GA) BASED CEED
GA is a global search method based upon the principle of natural selection. It combines an artificial, i.e. the Darwinian Survival of the fittest principle with genetic operation, abstracted from nature. The basic elements of the genetic algorithm are reproduction, crossover and mutation. To overcome the difficulties of classical methods, Sahu et al. [16] presented Genetic Algorithm based approach to solve economic load dispatch problem on IEEE 14 and IEEE 30 bus test cases and results are compared with quadratic programming by including the transmission losses. The results demonstrated the advancement of GA as compared to the conventional method.
Literature shows that GA is not limited to single objective problems. Guvenc [17] proposed genetic algorithm based algorithm on similarity crossover for solving combined economic and emission dispatch (CEED) problem in power system.
In this, offspring are created by using similarity measurement between mother and father chromosomes relationship. In the proposed method price penalty factor is used to convert multi-objective problem into single objective. This method has been tested on six and eleven generating unit system. And the results show that this technique can further be applied on complex unit commitment problems and dynamic CEED problems.
Damousis et al. [18] worked on real-coded GA to minimize the dispatch cost while satisfying generating unit and branch power-flow limits. In the proposed work, author used floating–point numbers for coding of the generator outputs instead of using binary representation. This method has not only improved the accuracy of the algorithm but also reduced the execution time. For comparison purposes, classical binary–coded GA scheme is also implemented. Results showed that RCGA provides the optimal solution and more efficient than the binary–coded GA.
Since most of the objectives are of conflicting nature in multi-objective problems, therefore a set of Pareto optimal solutions is obtained instead of obtaining a single solution. In such cases it is required that a best compromise solution out of available non-dominated solutions is to be selected. Parihar [19] introduced an approach based upon Fuzzy ranking to deal with multi-objective problem of fuel cost, emission and system loss minimization based RCGA.
Various multi-objectives GA based approaches such as Multi-objective Genetic Algorithm (MOGA), Vector Evaluated Genetic Algorithm (VEGA), Niched Pareto Genetic Algorithm (NPGA), Non-dominated Sorting Genetic Algorithm (NSGA), NSGA-II, are discussed in literature. The main working principles of these algorithms are to push the solutions towards Pareto-optimal front and to maintain diversity among the solutions in the Pareto-optimal front [20].
NSGA-II is a multi-objective genetic algorithm which is based upon non-dominated sorting scheme. The aim of the multiobjective optimization is to find solutions which are close to pareto-optimal solution and solutions should be as diverse as possible in the obtained non-dominated front. NSGA-II meets the both of the objectives as given by Deb et al. [21]. Purkayastha and Sinha [22] used NSGA-II algorithm for optimal combined economic and emission load dispatch. NSGA-II is used with adaptive crowding distance called modified NSGA-II which enhances the capability of creating more potential and diverse solutions. The proposed method is tested on a test case of 40 units for optimum combined economic and emission dispatch problem. And the results demonstrated that the algorithm is well competent to find the non-dominated solutions even for more than three objectives.
Horn et al. [23] proposed Niched Pareto Genetic Algorithm (NPGA) for solving multi-objective optimization problem. It is based upon tournament selection based Pareto dominance principle. In this method, for selecting winner, two individuals and a comparison set are selected at random from the population. Each selected individual will be tested with respect to the comparison set to select winner. If one candidate dominates the other, it will be selected as winner and the other will be selected for reproduction. If both or neither candidates are dominated, then winner will be selected by sharing. Abido [24] described the NPGA approach applied in environmental/economic power dispatch optimization problem. This method has diversity–preserving mechanism to find widely different pareto-optimal solution. A clustering technique is also implemented to provide the operator with a representative and manageable pareto-optimal set without destroying the characteristics of the trade-off front. And to find the best compromise solution over the trade-off curve, Fuzzy based technique is used.

PARTICLE SWARM OPTIMIZATION (PSO) BASED CEED
The concept of particle swarm optimization (PSO) was first given by Kennedy and Eberhart in 1995 [25]. It is based upon the principle of fish schooling and bird flocking. It is a population based method in which each individual is considered as particle and each particle represent the solution candidate. A swarm of individuals (particles) fly through the solution space. The position of particle is adjusted by the best position encountered by the particle itself or its neighbors. Many researchers have worked on applications of PSO in power system [26-28].
Conventional gradient method can be used for solving ED problem only if the fuel cost curves of the generating units are assumed to be piecewise linear and monotonically increasing in nature otherwise it will converge to suboptimal or infeasible solution. Classical PSO can handle all such problems but it suffers from premature convergence. Chaturvedi et al. [29] worked on PSO with time varying acceleration coefficient for non-convex economic dispatch to control the local and global search and to avoid premature convergence in classical PSO. Hamedi [30] proposed an advanced parallelized synchronous particle swarm optimization (PSPSO) algorithm for finding the optimal combination of power generation units that minimizes the fuel cost and emission. In this algorithm, positions and velocities are updated at the end of each iteration and the time required for solving CEED reduced substantially by using parallel computation. This algorithm can be performed efficiently when three conditions are met. First, the optimization has total and undivided access to a homogeneous cluster of computers without interruptions from the other user. Second, the analysis function takes a constant amount of time to evaluate any set of design variables throughout the optimization. Last, the number of parallel tasks can be equally distributed among the available processors.
Over past few years, there have been several proposals for extending PSO to multi-objective PSO and these methods are called multi-objective particle swarm optimization (MOPSO). Abido [31] proposed MOPSO technique by redefining the global best and global best individuals in multi-objective optimization domain. Clustering algorithm is used to manage the size of the Pareto-optimal set and fuzzy approach is used to extract the best compromise solution between minimum cost and less emission. This technique is found effective over other multi-objective techniques in terms of the quality of the obtained Pareto-optimal solutions.

STRENGTH PARETO EVOLUTIONARY ALGORITHM (SPEA) BASED CEED
Zitzler and Thiele [32] Proposed Strength Pareto Evolutionary Algorithm for multi-objective optimization that integrates the features of developed multi-objective EA’s in a unique manner. This technique stores externally the individuals that represent a non-dominated front among all the solutions considered so far. All the solutions in the external non-dominated set participate in the selection. In this algorithm concept of Pareto dominance is used in order to assign scalar fitness values to the individuals. The fitness of an individual is determined from the solutions stored in the external non-dominated set. In this approach, clustering procedure is incorporated to reduce the non-dominated set without destroying its characteristics and niching method is provided to preserve the diversity in the population. This is a pareto-based approach that does not require any distance parameter. Abido [33] used SPEA approach for environmental/economic power dispatch problem. In this approach, diversity-preserving mechanism is employed to overcome the premature convergence and search bias problem. A hierarchical clustering is imposed to provide the decision maker with a representative and manageable Paretooptimal set. The proposed technique is compared with classical techniques.

DIFFERENTIAL EVOLUTION (DE) BASED CEED
The concept of Differential Evolution (DE) was added in the family of evolutionary algorithms by Storn and Prince at Berkeley in 1995 [34]. DE is used for multidimensional real-valued functions and does not require derivatives of the objective function as in classical optimization method. The DE can be used in optimization problems where the objective function is stochastic, non-continuous, noisy, difficult to differentiate, change over time. The candidate solutions in DE are referred as agents. These agents are moved around in solution space to combine the position of existing agents from the population. If the new position of an agent is an enrichment, then it is accepted and becomes the part of the population otherwise the new position is rejected. The process is repeated until the best solution is not found. Soni and Bhuria [35] worked with DE algorithm for multi-objective emission constrained economic power dispatch problem. The search space is explored by randomly choosing the initial candidate solutions and using mutation, crossover and selection operators. The technique is found simple having compact structure and high convergence characteristics.
Multi-objective differential evolution (MODE) is the advancement of differential Evolution. In MODE, a pareto-based approach is used to implement the selection of the best individuals. Initially, a population is generated randomly and objective functions are evaluated. At a given generation of the evolutionary search in D-dimensional search space, the population is stored into several ranks based on non-dominated. Over the whole population the DE operators are carried out and then trial vector of same size as that of initial population is generated to make population size double than that of initial. Then the ranking of the combined population is carried out followed by crowding distance calculation. The best individuals are selected from combined population to retain initial population size. These individuals act as a parent vectors for the next generation. Basu [36] worked on the MODE algorithm for environmental economic load dispatch problem. The results obtained from the proposed algorithm have been compared with Pareto differential evolution and NSGA-II method.

ARTIFICIAL IMMUNE SYSTEM (AIS) BASED CEED
AIS [37] has been defined as Adaptive system inspired by theoretical immunology and observed immune functions, principles and models, which is applied to problem solving. Artificial immune system (AIS) is based upon the biological immune system that can be used for experimentation, explanation and prediction activities. The natural immune system is a complex and robust system that protects the human body from various foreign invaders. It is an adaptive system that maintains a state of equilibrium among various types of molecules, cells and tissues present in human body. It’s vital role is to detect the foreign invaders and act accordingly in order to neutralize their effect. The invading particles or pathogen known as antigen stimulates the immune system. Antigens may originate from within the body or the external environment leading to the production of antibodies.
An immunological system has main characteristics: proliferation, mutation, selection and memory which are used in large optimization techniques. Proliferation is the capability of generating new individuals. Mutation is process of searching for sub- optimum points through solution space. Selection eliminates the low affinity cells and memory stores the high affinity cells from the solution space and using this memory in new problem with an intension of reducing optimization time. These features make AIS a power tool for optimization process. Within AIS, there are different types of theories are developed which are based upon immune system such as: clonal selection, negative selection and immune network, somatic hypermutation etc. [38].
Rahman et al. [39] presented an application of Artificial Immune System using clonal selection principle to solve economic dispatch problem. The total generation cost is considered as an objective function and represented as the affinity measure. The antibodies with affinity measure are produced by genetic evolution. Before implementing the algorithm, few adaptations were made: there is no explicit antigen to be recognized, but an objective function is to be optimized; all the antibodies are to be selected for cloning; the number of cloned generated by the antibodies are equal. The algorithm is tested on binary and real number representation.

CONCLUSION
Many limitations such as large computational time, getting trapped into local minima, increasing computational complexity, non satisfactory results are experienced while working with classical methods on complex problems. The evolutionary methods have the capability to overcome such deficiencies of classical methods. In this paper, various advances in the field of evolutionary algorithms for solving combined economic/emission dispatch problem have been discussed. This paper includes the discussion on evolutionary methods based on Genetic algorithm, Particle Swarm Optimization, Differential Evolution, Strength Pareto Evolutionary Algorithm (SPEA) and Artificial Immune System.

Figures at a glance
Figure Figure Figure
Figure 1 Figure 2 Figure 3
 

References