Keywords
|
| Resonant Frequency, space-filling, wideband. |
INTRODUCTION
|
| In 1970, Dr B. Mandelbrot coined the term Fractal. Fractal symbolises broken or irregular fragments. He investigated the relationship between fractals and nature using discoveries made by Gaston Julia, Pierre Fatou, and Felix Hausdorff [1]-[2]. He was able to show that many fractals exist in nature and can be used to accurately model certain phenomena. Fractals describe a family of complex shapes that possess an inherent self-similarity in their geometrical structure. Fractal has various properties like recursive, infinite, space filling and self-symmetry [2]-[10]. Due to these properties fractals have more resonant frequency which contributes to lower return loss [17]. Hence less power is reflected back to the source and radiation emission is stronger. Fractal antennas are based on the concept of a fractal, which is a recursively generated geometry that has fractional dimensions. There are two active areas of research in fractal antenna engineering. The purpose of this article is to provide an overview of recent developments in the theory and design of fractal antenna elements, as well as fractal antenna geometries. Many fractal element antennas use the fractal structure as a virtual combination of capacitors and inductors. Due to this an antenna has many different resonances which can be chosen and adjusted by choosing the proper fractal design. |
GEOMETRIES OF FRACTAL ANTENNA
|
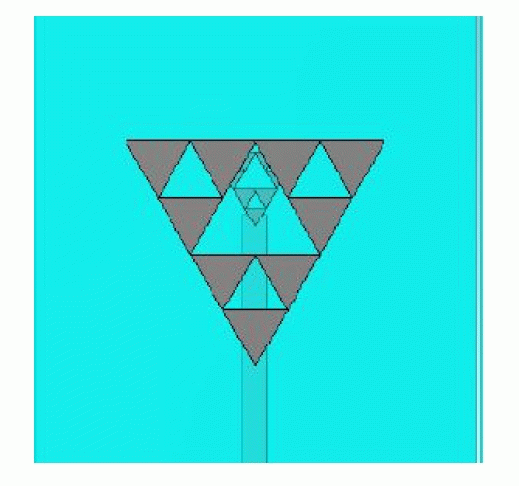
| A. The geometries of fractal antenna can be described and generated using an iterative process that leads to self affinity structures mentioned in [3]-[4]. These can be categorised in two types: Deterministic and random. Deterministic, like the Sierpinski gaskets and the von Koch snowflake, are constructed by several scaled-down and rotated copies of themselves [2]. Random fractals have elements of randomness which makes it possible to simulate natural phenomena. The first fractal geometry to be described is the Sierpinski gasket [5]. The initial few stages involved in the construction of the sierpinski gasket are shown in Fig. 1. The procedure for constructing this geometry of fractal begins with an equilateral triangle contained in the plane. The process is continued by removing the similar triangle from the former triangle. This iterative process is carried out an infinite number of times to form the Sierpinski-gasket fractal. It can be easily deduced from this definition that the sierpinski gasket is an example of self-similar fractal. A useful elucidation of Figure 1 is that the black triangle areas represent a metallic conductor, whereas the regions where metal has been removed are represented by the white triangle areas. |
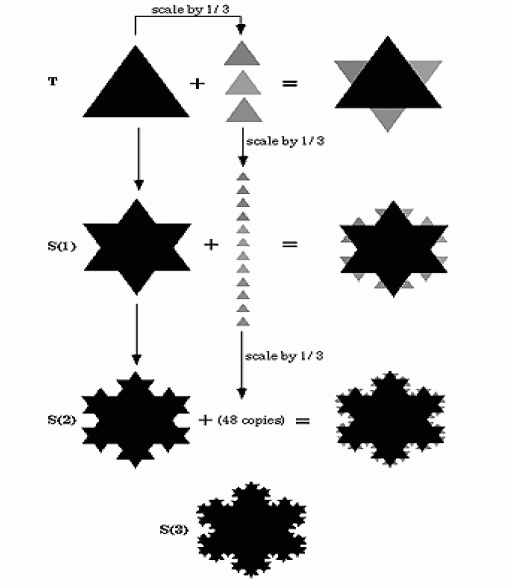
| However, in contrast to the Sierpinski gasket, which is constructed by the systematic removal of smaller and smaller triangles from the original structure in an iterative manner, the Koch snowflake is generated by adding smaller and smaller triangles to the original structure in an iterative manner. This procedure is clearly demonstrated in Fig. 2, where the first few stages involved in the construction of Koch snowflake geometry are shown. The above described geometries exhibit favourable radiation characteristics in terms of resonance, impedance and directivity. |
| B. Another fractal geometry which is popular is known as the Koch snowflake [5]. This geometry also begins as a solid equilateral triangle in the plane as demonstrated in ‘T’ of Fig. 2. |
LITERATURE REVIEW
|
| Puente et.al. (1996) demonstrated multiband behaviour for fractal Sierpinski gasket. They observed that this behaviour depends on the self-similarity properties of this gasket, which may propose an alternative way for the designing of new type of frequency independent and multiband antennas as shown in Fig. 5. |
| Yoonjae et.al. (2002) designed a novel conformal multiband fractal antenna, over triple band frequencies. They presented a Sierpinski fractal configuration, printed on a dielectric substrate of εr =4.3, on a ground plane, and suggested a different approach to improve its multiband performance in terms of radiation patterns, impedance matching having operatability in triple band frequency as well. |
| Douglas H. Werner and Suman Ganguly (2003) presented the overview of Fractal antenna engineering research. They described the combination of fractal geometry with electrodynamics and have elaborated the mathematical formulations. They elaborated the iterated function systems which are known as the language of fractals. |
| Raj Kumar et.al. (2007) demonstrated rectangular shaped fractal using proximity coupled feeding technique. The substrate is having dielectric constant εr =4.3, having height h= 1.53mm and with initial dimensions 36.08x29.6mm of rectangle patch. The size reduction of the patch antenna is explained by the fact that the experimental resonant frequency fr of fractal patch obtained with 2nd iteration is 2.11 GHz which is 2.42 GHz in rectangular patch. By incorporating 0.8mm air-gap in patch, the shrinkage bandwidth has been enhanced. Figure 7 shows the designed patch antenna. |
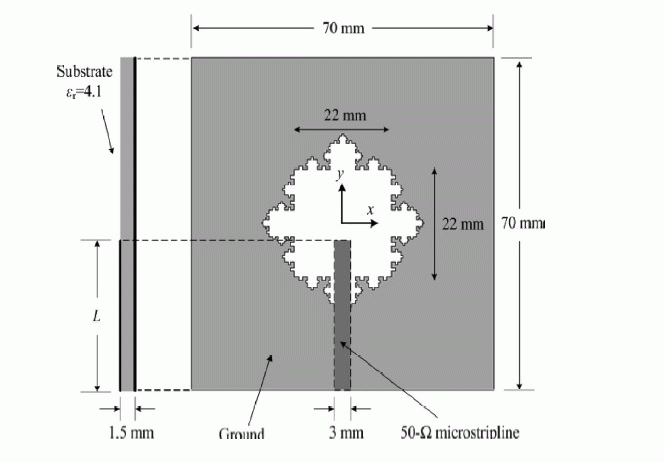
| Wen- Ling Chen et.al. (2009) suggested a wide fractal-shaped slot for enhancement of bandwidth using micro strip feeding technique. They experimentally studied the relation between the iteration order, iteration factor and bandwidth of the fractal shape. Experimental results show that it achieved a 2-dB gain bandwidth of 1.59 GHz which indicates that the impedance bandwidth, of this proposed fractal can attain an operating bandwidth of 2.4 GHz having operating frequencies approximately close to 4 GHz, which is nearly 3.5 times that of a conventional microstrip-line-fed antenna. Fig. 8 shows a designed microstrip antenna. |
| J. Malik and M. V. Kartikeyan (2011) suggested a small size antenna as compared to the Euclidean-type. They designed and studied an equilateral triangular patch antenna over the Sierpinski Gasket. For dual band WLAN application, two different patches are electromagnetically coupled having stacked structure and operating at two frequencies 2.4 GHz and 5.8 GHz. |
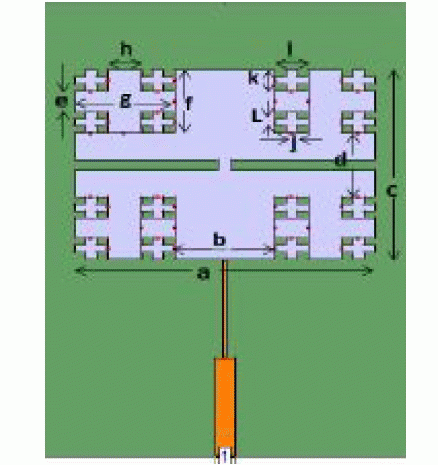
| Jagadeesha S. Vani et.al. (2012) suggested a multiband fractal antenna. This fractal uses two substrates having dielectric constant εr=4.4 mounted vertically over each other and having thickness of 1.6mm. This antenna radiates at multiple resonant frequencies. Fig. 10 shows the designed antenna. |
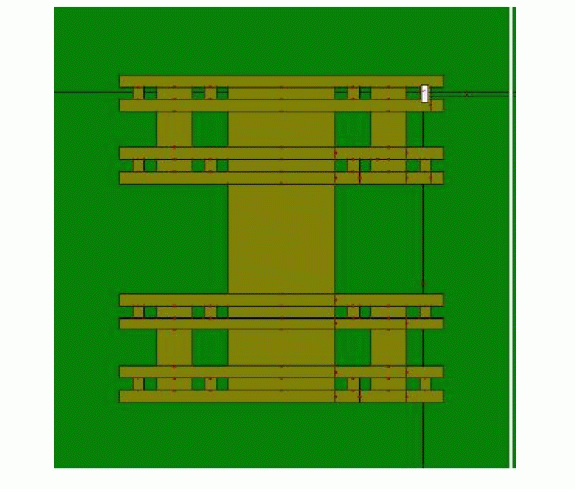
| Saurabh kohli et.al. (2013) demonstrated I shaped multiband fractal antenna. By application of three iterations on antenna, the resulting antenna resonates at 4.7 GHz, 6.5 GHz, 7.7 GHz and 8.5 GHz respectively having bandwidth 150 MHz, 135MHz, 520 MHz and 1.2 GHz. Its applications include defence and secure communication. Fig. 11 shows the designed antenna. |
CONCLUSIONS
|
| From the discussion, we have analysed the following key benefits of fractal in antenna geometry: |
| • With increasing number of iterations of fractal, resonant frequency increases which results in lower return losses. |
| • Multiband and broadband frequency response which is due to the inherent properties of the antenna’s fractal geometry. |
| • Compact size compared to the antennas having conventional designs, while maintaining god to excellent efficiencies and gains. |
| • Simplicity and mechanical robustness. Characteristics of fractal antenna are obtained due to its geometry and not by the addition of discrete components. |
| • Ability to design for particular multi-frequency characteristics containing specified stop bands as well as specific multiple pass bands. |
| We have concluded that triangular shaped fractal antenna has more bandwidth and operating frequency than other fractal shapes. Fractal antenna engineering research field is in the early stages of development. |
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
|
| |
References
|
- X. Yang, J. Chiochetti, D. Papadopoulos, and L. Susman, “Fractal Antenna Elements and Arrays,” Appl. Microwave Wireless, Vol. 11, no. 5, pp.34-46, May 1999.
- E. –O. Peitgen and D. Saupe (eds), The science of Fractal Images, Springer-verlag, Berlin/ New York, 1988.
- J. P. Gianvittoria and Y. Rahmat-samii, “Fractal Antennas: A Novel Antenna Miniaturization Technique, and Applications,” IEEE AntennasPropagation Magazine, Vol. 44, No. 1, pp. 20-36, February 2002.
- J. P. Gianvittoria and Y. Rahmat-samii, “Fractal Element Antennas: A complication of Configurations with Novel Characteristic,” 2000 IEEEAntennas and propagation Society International Symposium, Vol. 3, Salt Lake City, Utah, pp. 1688-1691, July 16-21, 2000.
- H. O. Peitgen, H. Jurgens, and D. Saupe, Chao and Fractal: New Frontiers of Science, New York, Springer-verlag, Inc., 1992.
- D. H. Werner, R. L. Haupt, and P. L. Werner, “Fractal Antenna Engineering: The Theory and Design of Fractal Antenna Arrays,” IEEE AntennasPropagation Magazine, Vol. 41, No. 5, pp. 37-59, October 1999.
- Douglas H. Werner, and SumanGanguly, “An Overview of Fractal Antenna Engineering Research,” IEEE Antennas and Propagation Magazine,Vol. 45, No. 1, pp. 38-57, February 2003.
- Raj Kumar, P. Malathi, and J. P. Shinde, “Design of Miniaturized Fractal Antenna,” 37th European Microwave Conference, October 2007.
- J. Malik, and M. V. Kartikeyan, “A Stacked Equilateral Triangular Patch Antenna with Sierpinski Gasket Fractal for WLAN Applications,”Progress In Electromagnetic Research Letters, Vol. 22, pp. 71-81, March 2011.
- Constantine A. Balanis, “Antenna Theory,” John Wiley & Sons, Inc., 2012.
- Jagadeesha S., Vani R. M. And P. V. Hunugund, “Stacked Plus Shape Fractal Antenna for Wireless Application,” IJECET, Vol. 3, Issue 1, pp.286-292, January-June 2012.
- Saurabhkohli, Sukhwinder Singh Dhillon, and AnupamaMarwaha, “Design and Optimization of Multiband Fractal Microstrip Patch Antenna forWireless Application,” IEEE computer society, 2013.
- SundaramAnanth, MaddelaMadhurima and Ramadoss Ramesh, “Koch-Fractal Folded-Slot Antenna Charateristics,” IEEE Antenna and WirelessPropagation Letters, Vol. 6, pp. 219-222, 2007.
- C. Puente et.al, “Fractal Multiband Antenna based on the Sierpinski Gasket,” Electronics Letters, Vol. 32, pp. 1, January 1996.
- Yoonjae et.al, “A Novel Conformal Multiband Antenna Design based on Fractal concepts,” IEEE, pp. 92-95, 2002.
- Wen-Ling Chen et.al, “Bandwidth Enhancement of a Microstrip-Line-Fed Printed Wide-Slot Antenna With a Fractal-Shaped Slot,” IEEETRANSACTIONS ON ANTENNAS AND PROPAGATION, Vol. 57, No. 7, July 2009.
- Wikipedia, “Resonant frequency,”
|