Keywords
|
| Commensal, equilibrium state, host, stable, oscillatory. |
INTRODUCTION
|
| Ecology is the study of the interactions between organisms and their environment. The organisms include animals and plants, the environment includes the surroundings of animals. So ecology relates to the study of living beings (animals and plants) in relation to their habits and habitats. This discipline of knowledge is a branch of evolutionary biology purported to explain how or to what extent the living beings are regulated in nature. Allied to the problem of population regulation is the problem of species distribution- prey-predator, competition, commensalism and so on. |
| Mathematical modeling has been playing an important role for the last half a century in explaining several phenomena concerned with individuals and groups of populations in nature. Significant research in the field of theoretical ecology has been formulated by Lotka[13] and by Volterra [17]. Since then, several mathematicians and ecologists contributed to the growth of this area of knowledge. |
| The general concept of modeling has been presented in the treatises of Freedman[6], Braun [5], Paul Colinvaux[14] and Kapur[11]. Srinivas[16] studied competitive ecosystem of two species and three species with limited and unlimited resources. Later, Lakshminarayan [12] studied prey-predator ecological model with partial cover for the prey and alternate food for the predator. Stability analysis of competitive species was carried out by Archana Reddy, Pattabhi Ramacharyulu and Krishna Gandhi [3] and by Bhaskara Rama Sarma and Pattabhi Ramacharyulu [4]. Acharyulu KVLN and Pattabhi Ramacharyulu[1], [2] obtained fruitful results on some Mathematical models of ecological Ammensalism. Phani Kumar [15] studied some mathematical models of ecological commensalism. The present author Hari Prasad [7] - [10] et al, discussed three and four species ecological models. |
| The present investigation is a study on discrete model of three species (S1, S2, S3) syn-eco system. The system comprises of a commensal (S1), two hosts S2 and S3 . Commensalism is a symbiotic interaction between two or more populations which live together, and in which only one of the populations (commensalism) is benefited while the other(host) is not effected, for example the clownfish shelters among the tentacles of the sea anemone, while the sea anemone is not affected.. |
BASIC EQUATIONS OF THE MODEL
|
| A. NOTATION ADOPTED |
| S1 : Commensal of S2 and S3 |
| S2 : Host of S1 and commensal of S3 |
| S3 : Host of S1 and S2 |
| Ni(t) : The population strength of Si at time t, i = 1,2,3. |
| t : Time instant. |
| ai : Natural growth rate of Si , i = 1,2, 3. |
| a33 : Self inhibition coefficient of S3. |
| a12, a13 : Interaction coefficients of S1 due to S2 and S1 due to S3. |
| a23 : Interaction coefficient of S2 due to S3 |
| Further the variables N1, N2, N3 are non-negative and the model parameters a1, a2, a3, a33, a12 , a13, a23 are assumed to be non-negative constants. |
| B. BASIC EQUATIONS |
| Consider the growth of the species during the time interval (t, t + 1). |
| Equation for the first species (N1): |
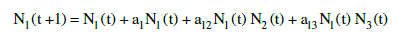 (1) (1) |
| Equation for the second species (N2): |
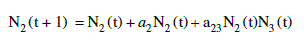 (2) (2) |
| Equation for the third species (N3): |
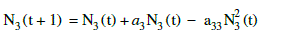 (3) (3) |
| Species-Growth equations in the discrete form: |
| The discrete form of the three species syn ecological model is |
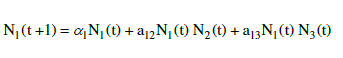 (4) (4) |
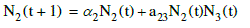 (5) (5) |
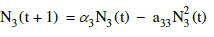 (6) (6) |
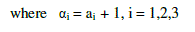 (7) (7) |
EQUILIBRIUM STATES
|
| For a continuous model the equilibrium states are defined by i dN = 0, i = 1,2,3 dt , the equilibrium states for a discrete model are defined in terms of the period of no growth. |
| i.e, Ni(t + r) = Ni(t) , r = 1,2,3,……….., where r is the period of the equilibrium state. |
| A. ONE PERIOD EQUILIBRIUM STATES (STAGE-I) |
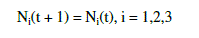 (8) (8) |
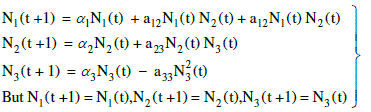 (9) (9) |
| The system under investigation has two equilibrium states given by |
| (i) Fully washed out state |
| E : N ? 0, N ? 0, N ? 0 |
| (ii) The state in which only the third species survives |
| E : N = 0, N = 0, N = ,when 1 |
| B. STABILITY OF EQUILIBRIUM STATES |
| Stability of E1(0,0,0): |
| N1(t) = N1(t +1) = N1(t +2) = …………………= 0 |
| N2(t) = N2(t +1) = N2(t +2) = …………………= 0 |
| N3(t) = N3(t +1) = N3t +2) = …………………..= 0 |
| i.e. Ni(t + r)=0, where r is an integer and i = 1,2,3 |
| Hence, E1(0,0,0) is stable. |
| Stability of E2: |
| N1(t) = N1(t +1) = N1(t +2)= …………………= 0 |
| N2(t) = N2(t +1) = N2(t +2)= …………………= 0 |
| N3(t) = N3(t +1) = N3(t +2)= …………………= 3 |
| i.e. Ni(t + r) = 0, N3(t + r) = 3 33 1 a ? ? , where r is an integer and i = 1,2 |
| Hence, E2 is stable. |
| At this stage all the two equilibrium states E1, E2 are stable. |
| C. TWO PERIOD EQUILIBRIUM STATES (STAGE-II) |
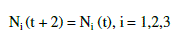 (10) (10) |
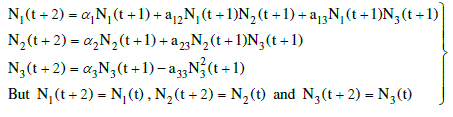 (11) (11) |
| The system under investigation has five equilibrium states given by |
| (i) Fully washed out state |
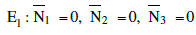 |
| (ii) States in which only the third species survives |
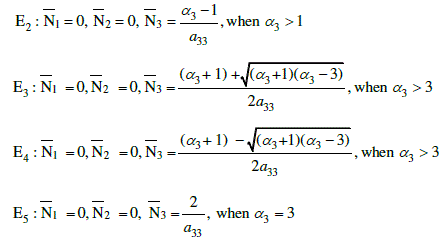 |
| The states E3 and E4 coincide 3 when ? ? 3 and do not exist 3 when ? ? 3 . |
| D. STABILITY OF EQUILIBRIUM STATES |
| The equilibrium states E1 and E2 are stable as established in III-B. Now we will discuss the stability of other equilibrium points except these two points in this stage. |
| Stability of E3: |
| N1(t) = N1(t +1) = N1(t +2) = …………………= 0 |
| N2(t) = N2(t +1) = N2(t +2) = …………………= 0 |
| i.e. Ni(t + r) = 0, where r is an integer and i = 1,2 |
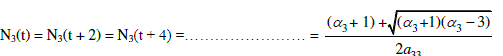 |
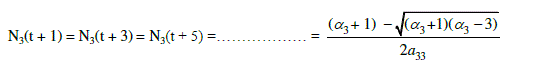 |
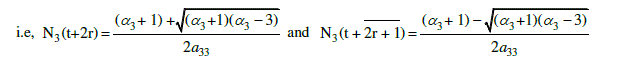 |
| where r is an integer. |
| and is stable when 3 ? ? 3 . |
| Stability of E4: |
| N1(t) = N1(t +1) = N1(t +2) = ………………= 0 |
| N2(t) = N2(t +1) = N2(t +2) = ………………= 0 |
| i.e. Ni(t + r) = 0, where r is an integer and i = 1,2 |
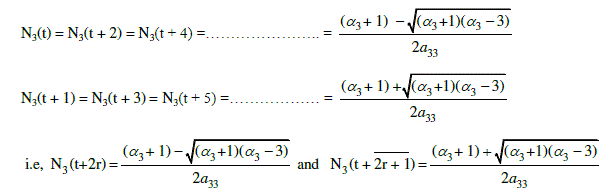 |
| where r is an integer. |
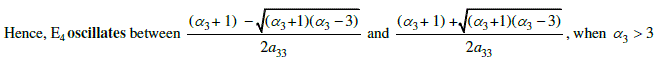 |
| and is stable when 3 ? ? 3 . |
| Stability of E5: |
| N1(t) = N1(t + 1) = N1(t + 2) = …………………..= 0 |
| N2(t) = N2 (t + 1) = N2 (t + 2) = …………….…….= 0 |
| N3(t) = N3(t + 1) = N3(t + 2) = …………….………= 33 |
| i.e, Ni(t + r) = 0, N3(t + r) = 33 2 a , where r is an integer and i = 1,2 |
| Hence, E5 is stable. |
| At this stage, in all five equilibrium states, only the three equilibrium states E1 , E2 , E5 are stable and other two E3 , E4 are oscillatory. |
NUMERICAL EXAMPLES
|
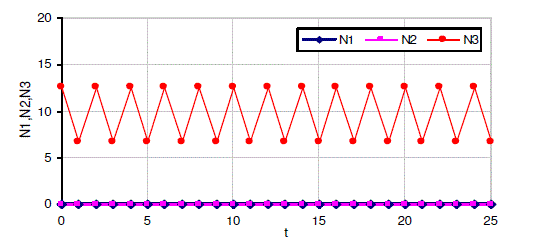
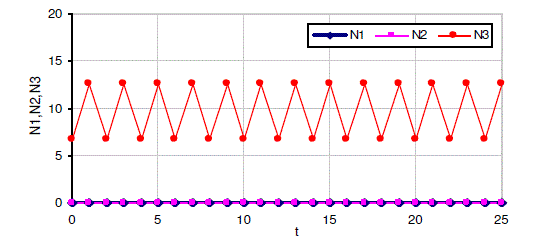
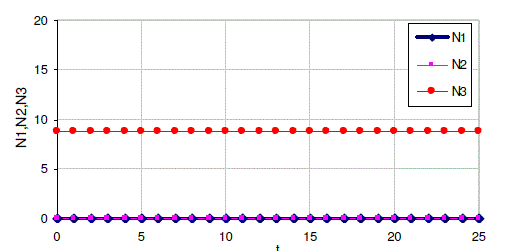
| The numerical solutions of the discrete model equations (4), (5) and (6) computed for specific values of the various parameters and the initial conditions. For this MS EXCEL has been used and the results are illustrated in Figures 1 to 5. |
CONCLUSION
|
| The present paper deals with an investigation on a discrete model of three species syn eco-system. The system comprises of a commensal (S1), two hosts S2 and S3 ie., S2 and S3 both benefit S1, without getting themselves effected either positively or adversely. Further S2 is a commensal of S3, S3 is a host of both S1, S2 and the first and second species have unlimited resources. All possible equilibrium points of the model are identified based on the model equations at two stages. |
| Stage-I : ? ? ? ? i i N t +1 = N t ; i = 1, 2 |
| Stage-II : ? ? ? ? i i N t + 2 = N t ; i = 1, 2 |
| In Stage-I there are only two equilibrium points, while the Stage-II there would be five equilibrium points. All the two equilibrium points in Stage-I are found to be stable while in stage-II only three are stable. Further the numerical solutions for the discrete model equations are computed. |
ACKNOWLEDGMENT
|
| I thank to Professor (Retd), N.Ch.Pattabhi Ramacharyulu, Department of Mathematics, NIT, Warangal (A.P.), India for his valuable suggestions and encouragement. Also I acknowledge to Mr.K.Ravindranath Gupta for neat typing for this research paper. |
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
|
| |
References
|
- AcharyuluK.V.L.N.and N.Ch PattabhiRamacharyulu.;“On The Stability Of Harvested Ammensal - Enemy Species Pair With LimitedResources”, International Journal of Logic Based Intelligent Systems, Vol. 4, No. 1,pp.1-16,Jan-June 2010.
- Acharyulu K.V.L.N.& N.Ch PattabhiRamacharyulu.; “An Ammensal-Prey with three species Ecosystem”, International Journal ofComputational Cognition , Vol.9, No.2, pp.30-39, june2011.
- Archana Reddy R., Pattabhi Rama Charyulu N.Ch., and Krisha Gandhi B, A Stability Analysis of Two Competetive Interacting Specieswith Harvesting of Both the Species at a Constant Rate, Int. J. of Scientific Computing 1 (1), 57 – 68, 2007.
- Bhaskara Rama Sharma B and Pattabhi Rama Charyulu N.Ch., Stability Analysis of Two Species Competitive Eco-system, Int.J.of LogicBased Intelligent Systems 2(1), 2008.
- Braun, M.: “Differential Equations and their Applications-Applied Mathematical Sciences”, (15), Springer, New York, 1978.
- Freedman,H.I.: “Deterministic Mathematical Models in Population Ecology”, Marcel-Decker, New York, 1980.
- Hari Prasad, B. and PattabhiRamacharyulu, N. Ch.: “On the Stability of a typical three species syn eco-system”, International Journal ofMathematical Archive, 3(10), pp: 3583-3601, 2012.
- HariPrasad.B and Pattabhi Ramacharyulu.N.Ch., On the Stability of a Four Species : A Prey-Predator-Host-Commensal-Syn Eco-System-VII (Host of the Prey Washed Out States), Int. Journal of Applied Mathematical Analysis and Applications, Vol.6, No.1-2, pp.8594,2011.
- HariPrasad.B and Pattabhi Ramacharyulu.N.Ch., On the Stability of a Four Species Syn Eco-System with Commensal Prey Predator Pairwith Prey Predator Pair of Hosts-VII (Host of S2 Washed Out States), Journal of Communication and Computer, Vol.8, No.6, pp.415 –421, 2011.
- Hari Prasad, B. and PattabhiRamacharyulu, N. Ch.: “Global Stability of Four Species Syn Eco-System: A Prey-Predator-Host-Commensal- A Numerical Approach”, International Journal of Mathematics and Computer Applications Research, Vol.3, Issue.1, pp:275-290, 2013.
- Kapur J. N., Mathematical Modelling in Biology and Medicine, Affiliated East West, 1985.
- Lakshmi Narayan K., A Mathematical Study of a Prey-Predator Ecological Model with a partial cover for the Prey and Alternate Food forthe Predator, Ph.D. Thesis, JNTU, 2005.
- Lotka A. J., Elements of Physical Biology, Williams and Wilking, Baltimore, 1925.
- Paul Colinvaux A., Ecology, John Wiley, New York, 1986.
- Phani Kumar N, Some Mathematical Models of Ecological Commensalism, Ph.D., Thesis, A.N.U. 2010.
- Srinivas N. C., “Some Mathematical Aspects of Modeling in Bio-medical Sciences” Ph.D Thesis, Kakatiya University, 1991.
- Volterra V., Leconssen La TheorieMathematique De La LeittePouLavie, Gauthier-Villars, Paris, 1931.
|