Keywords
|
| Gene expression, optimization, fitness function, encoding, chromosome, selection, cross over, mutation, Particle swarm |
INTRODUCTION
|
| Gene expression is the method in which information from gene is used for the generation of gene product. The genetic code of a sample is interpreted by gene expression data. Genes carry information regarding the building and maintain of cells for an organism. The nucleotide subunits are namely adenine, cytosine, guanine and thymine. Guanine, Cytosine and Adenine, Thymine pairs respectively. The expression levels of various genes can be represented by using Microarray technology.DNA molecules of various genes are placed in discrete spots of a microscope slide. A simple microarray is an N×M array, where N is the number of genes and M is the number of conditions. Each row in the array represents a gene and columns represent the conditions. |
| Data mining is an area, where we can extract knowledge from a large database. Extraction of knowledge can be done by various data mining tasks. One of the important data mining tasks is clustering which is having a number of applications in the area of biology and other disciplines. There are mainly two methods of clustering. The first one is hierarchical method and the other one is partitional method. Optimization denotes either minimization or maximization. It determines the minimum or maximum of a real valued function. From an optimization point of view, clustering is a kind of NP hard grouping problem. This encouraged the search of efficient evolutionary algorithms. In an optimization problem, the function F is called fitness function or objective function. |
| A. Fitness Function |
| A fitness function is a type of objective function used to summarize, as a single figure of merit, how close a given design solution is to achieving the set aims. Many of the validity criteria in clustering can be used for evaluating partition containing a given number of clusters. These criteria’s can be used as fitness functions to evolve data partitions. |
| B. Encoding |
| There are many encoding schemes available. Some of the important encoding schemes are binary encoding, integer encoding and real encoding. |
Integer encoding: Clustering solutions can be represented in two ways by integer encoding. In the first one, an integer vector of N position is considered as a genotype where N is the number of dataset objects. Each position corresponds to a particular object ie, ith gene represent the ith dataset object provided that a genotype represents a partition formed by k clusters. So each gene will have a value between 1 and k. These values represent the cluster label, for example the clustered integer vector can be represented as [1111222233 1111222233]. The integer encoding scheme is naturally redundant approach, because the encoding is one-to-many. In fact the same solution can be represented by different k! genotypes. For example 3! genotypes can correspond to same clustering solution represented as [1111333322 1111222233]. The integer encoding scheme is naturally redundant approach, because the encoding is one-to-many. In fact the same solution can be represented by different k! genotypes. For example 3! genotypes can correspond to same clustering solution represented as [1111333322 1111333322],[1111222233 1111333322],[1111222233 1111222233], [2222333311 1111222233], [2222333311 2222333311], [2222111133 2222333311], [2222111133 2222111133], [3333111122 2222111133], [3333111122 3333111122] and [3333222211 3333111122] and [3333222211 3333222211]. 3333222211]. |
RELATED WORKS
|
| Holland [12] devised Genetic Algorithm which is proved to be efficient in solving combinatorial optimization problems. Operations such as selection, cross-over and mutation are performed in the algorithm. |
| Spendley et al ., (1962) proposed a simple search method which is modified by Nelder and Mead (1965). The modified method was an unconstrained and non-linear. In the simplex Nelder Mead method, the coordinate with highest function value is replaced with a reflected or extended alternate point. Iteratively changing the coordinate with maximum function value will finally result in an optimum point. |
| G. Syswerda [9] (1993) introduced a method called bit-based simulated crossover in genetic algorithm which uses a statistics in population of GA to generate offspring. |
| Joines et al [7] introduced a hybrid technique using GA and local improvement methods to solve issues in cell design problems [3]. The main aim of his work is to form a set of autonomous units in which inter-cell movement of parts are minimized. Kennedy and Eberhart (1995) introduced a random search technique based on population called Particle Swarm Optimization (PSO) which is motivated by the behavior of organisms like bird flock. |
| Harik et al ., [8] (1997) pointed the convergence of GA in some special class of problems which includes nonoverlapping and tightly coded building blocks. Renders et al .,[10] (1996) proposed a hybrid method using genetic algorithm for global optimization. It mentioned about the trade-off between reliability, accuracy and computation time. Marco et al ., (2004) [11] introduced a globalized Nelder Mead method for the optimization purpose. Here globalization is achieved by a method called probabilistic restart and local searches are performed by improved Nelder Mead algorithm. |
| Sun et al., (2004a, 2004b, 2005) [2] [3] [4] introduced a new variant of PSO, called Quantum-behaved Particle Swarm Optimization (QPSO), which is proposed in order to improve the global search ability of PSO. The QPSO uses a different equation when compared to PSO and it needs no velocity vectors for particles, and has fewer parameters to adjust and can be implemented more easily. Shu-Kai et al ., (2006) proposed a combination of algorithm which contains GA and PSO which is hybridized with Nelder Mead. It demonstrated the possibility and potential of integrating Nelder Mead with GA or PSO. |
| Fang et al., (2010) [5] proved that the iterative equation leads QPSO to be global convergent. The QPSO algorithm has been aroused the interests of many researchers from different communities. |
GENETIC ALGORITHM
|
| Genetic Algorithm (GA) is a search heuristic that mimics the process of natural evolution [12]. Genetic algorithm is an evolutionary algorithm (EA) inspired by natural evolution, which provides solutions to optimization problems. The main steps in genetic algorithm include initialization, selection, crossover, mutation. This is mainly used to generate useful solutions in optimization and search problems. |
| The evolution process starts from a randomly selected population. This population will get evolved after centauries. In each generation, the fitness of every individual in the population is evaluated, and selection of multiple individuals is performed from the current population based on their fitness. A new population is formed by performing mutation. In the next iteration of the algorithm, the new population is used. |
| The main steps involved in Genetic Algorithm are: |
| A. Selection |
| During each successive generation, a set of existing population is selected to breed a new generation. Using fitness based process, individual solutions are selected and the individuals with fitter solutions (as measured by a fitness function) are typically selected for evolution. Certain selection methods will rate the fitness of each solution and based on the rating possible set of best solutions are selected. |
| B. Cross-over |
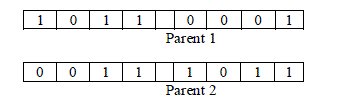
| In genetic algorithms, to vary the programming of a chromosome or set of chromosomes from one generation to next, we can make use of a genetic operator called crossover. Crossover is the process of taking more than one parent solutions and producing a child solution from them. Given two parents, single-point crossover will generate a cut-point and recombines the first part of first parent with the second part of the second parent and create a new offspring. Single-point crossover then recombines the second part of the first parent with the first part of the second parent to create a second offspring. (See figure 1 and 2). |
| C. Mutation |
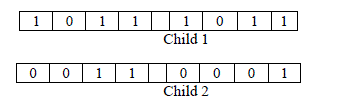
| After selection and crossover, a new population full of individuals is obtained. Some are copied, and others are produced by crossover. To make sure that the individuals are not all exactly the same, mutation is applied. First check through all the genes of the individuals, and if that gene is selected for mutation, it can be changed slightly or replace it with a new value. A visual for mutation is shown below. Mutation is fairly simple. We just change the selected genes based on what you feel is necessary and move on. Genetic diversity is ensured by using mutation. (See figure 3 and 4). |
PARTICLE SWARM OPTIMIZATION
|
| Dr. Eberhart and Dr. Kennedy [1] developed a population based stochastic optimization technique called Particle swarm optimization (PSO) in 1995, inspired by social behavior of bird flocking. PSO shares many similarities with evolutionary computation techniques such as Genetic Algorithms (GA). A population of random solution is used to initialize the system and searches for optima by updating generations. Unlike GA, PSO has no evolution operators such as crossover and mutation. In PSO, the particles fly through the problem space by following the current optimum particles. |
| PSO resembles the behaviors of bird flock searching for food. Consider a group of birds are randomly searching food in an area. There is only one piece of food in the area being searched. All the birds do not know where the food is but in each iteration they will know how far the food is at. So the best strategy to find the food is to follow the bird which is nearest to the food. All particles have fitness values which are evaluated by the fitness function to be optimized, and have velocities which direct the flying of the particles. The particles fly through the problem space by following the current optimum particles. |
| PSO is initialized with a group of random particles (solutions) and then searches for optima by updating generations. In every iteration, each particle is updated by following two "best" values. The first one is the best solution (fitness) it has achieved so far. (The fitness value is also stored.) This value is called pbest. Another "best" value that is tracked by the particle swarm optimizer is the best value, obtained so far by any particle in the population. This best value is a global best and called gbest. When a particle takes part of the population as its topological neighbors, the best value is a local best and is called lbest. |
| The velocity and position of the particle is updated using equation (a) and (b) when two best values are found. |
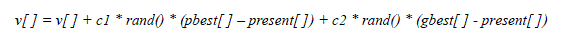 (4.1) (4.1) |
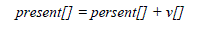 (4.2) (4.2) |
| Where, v[] is the particle velocity, persent[] is the current particle (solution). pbest[] and gbest[] are defined as stated before. rand () is a random number between (0,1). c1, c2 are learning factors which is usually c1 = c2 = 2. |
NELDER MEAD SIMPLEX METHOD
|
| Nelder Mead simplex algorithm [6], is an algorithm that exploits local information and converges to the nearest optimal point. It is an algorithm searching for local minimum and can be used for multi-dimensional optimizations. |
| Nelder and Mead devised a simplex method for finding a local minimum of a function of several variables. For two variables, a simplex is a triangle, and the method is a pattern search that compares function values at the three vertices of a triangle. The worst vertex, where f (x, y) is largest, is rejected and replaced with a new vertex. A new triangle is formed and the search is continued. The process generates a sequence of triangles (which might have different shapes), for which the function values at the vertices get smaller and smaller. |
| A. Initial Triangle BGW |
| Let f (x, y) be the function that is to be minimized. To start, we are given three vertices of a triangle: Vk = (xk , yk), k = 1, 2, 3. The function f (x, y) is then evaluated at each of the three points: zk = f (xk , yk) for k = 1, 2, 3. The subscripts are then reordered so that z1 ≤ z2 ≤ z3. We use the notation |
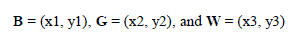 |
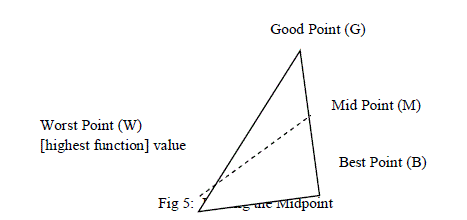
| B. Midpoint of the Good Side |
| The construction process uses the midpoint of the line segment joining B and G. (see Figure 5). It is found by averaging the coordinates: |
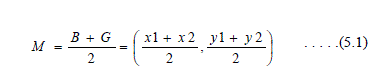 |
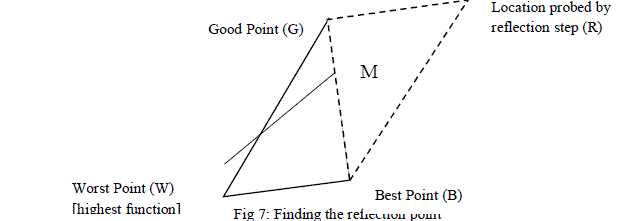
| C. Reflection Using the Point R |
| The function decreases as we move along the side of the triangle from W to B, and it decreases as we move along the side from W to G. Hence it is feasible that f (x, y) takes on smaller values at points that lie away from W on the opposite side of the line between B and G. |
| We choose a test point R that is obtained by “reflecting” the triangle through the side BG. (see Figure 7). The vector formula for R is |
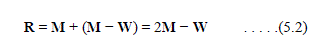 |
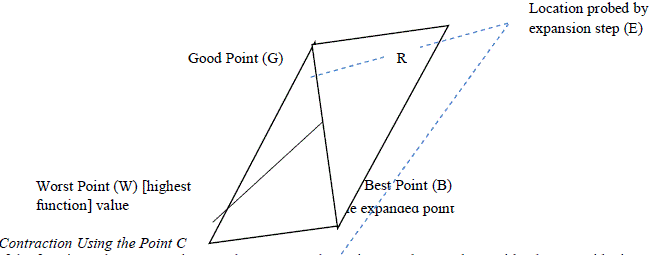
| D. Expansion Using the Point E |
| If the function value at R is smaller than the function value at W, then we have moved in the correct direction toward the minimum. Perhaps the minimum is just a bit farther than the point R. So we extend the line segment through M and R to the point E. (see Figure 7).The vector formula for E is |
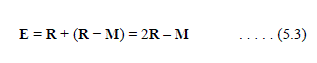 |
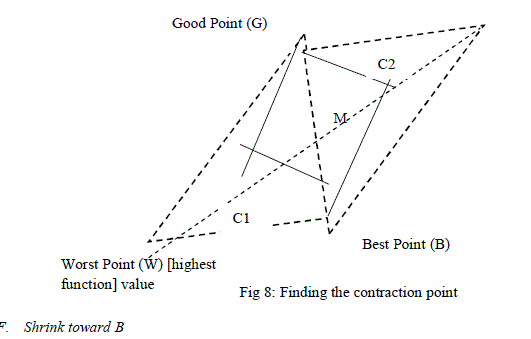
| E. Contraction Using the Point C |
| If the function values at R and W are the same, another point must be tested. Consider the two midpoints C1 and C2 of the line segments WM and MR, respectively (see Figure 8). |
| The point with the smaller function value is called C, and the new triangle is BGC. Note. The choice between C1 and C2 might seem inappropriate for the two-dimensional case, but it is important in higher dimensions. |
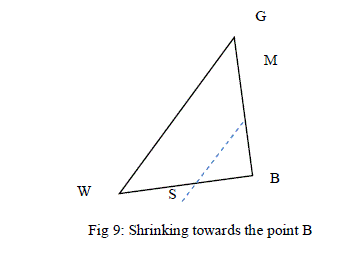
| F. Shrink toward B |
| If the function value at C is not less than the value at W, the points G and W must be shrunk toward B (see Figure 9). The point G is replaced with M, and W is replaced with S, which is the midpoint of the line segment joining B with W. |
| G. Logical Decisions for Each Step |
| A computationally efficient algorithm should perform function evaluations only if needed. In each step, a new vertex is found, which replaces W. As soon as it is found, further investigation is not needed, and the iteration step is completed. |
CONCLUSION
|
| Clustering of gene expression data can be done using many algorithms. Genetic algorithm uses nature inspired evolution to devise the optimization process. In a similar way PSO is also a nature inspired algorithm which makes use of parameters Pbest and Gbest to perform optimization. Nelder Mead is an optimization method based on number of points, in this paper we considered only 2 points so we get a triangle and optimization is performed based on those vertices. If more than 2 points are given the multi dimensional Nelder Mead can be applied for that polygon. Among the three algorithm Genetic algorithm gives more accurate result while only Nelder Mead can be used directly over a noisy data. |
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
|
| |
References
|
- Kennedy,J., Eberhart, R., 1995.Particle Swarm Optimization, In Proceedings of the IEEE International Conference on Neural Network, pp. 1942–1948.
- Sun, J., Feng, B., Xu, W.-B., 2004a. Particle swarm optimization with particles having quantum behavior, in Proceedings of Congress onEvolutionary Computation, June 2004, pp. 325–331.
- Sun, J., Xu, W.-B., Feng, B., 2004b. A global search strategy of quantum-behaved particle swarm optimization. In Proceedings of IEEE Conferenceon Cyber-netics and Intelligent Systems, December 2004, pp. 111–116.
- Sun, J., Xu, W.-B., Feng, B., 2005. Adaptive parameter control for quantum-behaved particle swarm optimization on individual level. In:Proceedings of IEEE International Conference on Systems, Man and Cybernetics, October 2005, pp. 3049–3054.
- Fang, W., Sun, J., Xie, Z., Xu, W, 2010. Convergence analysis of quantum-behaved particle swarm optimization algorithm and study on its controlparameter. Acta Phys. Sin. 59 (6), 3686–3694.
- N. Durand, J.M. Alliot, A combined Nelder–Mead simplex and genetic algorithm, in: W. Banzhaf, J. Daida, A.E. Eiben, M.H. Garzon, V. Honavar,M. Jakiela, R.E. Smith (Eds.), Proceedings of the Genetic and Evolutionary Computation Conference GECCO_99, Morgan Kaufmann, Orlando,FL, USA, 1999, pp. 1–7.
- J.A. Joines, M.G. Kay, R.E. King, A hybrid-genetic algorithm for manufacturing cell design. Technical Report NCSU-IE, Department of IndustrialEngineering, North Carolina State University, Box 7906 Raleigh, NC 27695-7906, February 1997.
- Harik, E. Cant´u-Paz, D. E. Goldberg, and B. Miller, “The gambler’s ruin problem, genetic algorithms, and the sizing of populations,” in Proc. 4thInt. Conf. Evolutionary Computation, T. B¨ack, Ed. Piscataway, NJ: IEEE Press, 1997, pp. 7–12.
- G. Syswerda, “Simulated crossover in genetic algorithms,” in Foundations of Genetic Algorithms 2, L. D. Whitley, Ed. San Mateo, CA: MorganKaufmann, 1993, pp. 239–255.
- J.M. Renders, S.P. Flasse, Hybrid method using genetic algorithms for the global optimization, IEEE Transactions on Systems, Man, andCybernetics 26 (2) (1996) 243–258
 (1996) 243–258. (1996) 243–258.
- Marco A. Luersen and Rodolphe Le Riche, “GlobalisedNelder-Mead method for Engineering optimization”, Journal of computers and structures,Vol 3, 2004, 10 pages.
- J.H. Holland, Adaptation in natural and artificial systems, University of Michigan Press, Ann Arbor, MI, Internal report, 1975.
|