A Survey: FP Tree Algorithm with and Without
Trusted Party for Environmentally Distributed
Databases

Raghvendra Kumar; Ashish Jaiswal; Divyarth Rai

A Survey: FP Tree Algorithm with and Without Trusted Party for Environmentally Distributed Databases

Raghvendra Kumar, Ashish Jaiswal ,Divyarth Rai
Dept of Computer Engineering LNCT Group of College Jabalpur, M.P., India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Data mining technology has emerged as a means of Identifying patterns and trends from large quantities of data. Mining rule is important data mining problem .To solve mining rule problem many technique are available example Apriori, FP Tree. FP Tree Algorithm has wide distribution to find relationship between among the attribute in database. The privacy concept arises when the data is distributed in the environment, concept of privacy arises here so that no any unauthorized person not able to decrypt the data and see the result. For this we used hash based secure sum cryptography technique because when the party to find the global result may be that result is frequent or infrequent. That’s why privacy concept is arises with and without trusted party. In this paper we compare the result privacy preserving technique with and without trusted party for horizontal partitioned database with the help of FP Tree Algorithm. And provide high privacy to database with percentage of data leakage is zero percent.

Keywords

Data mining, Distributed database, Privacy preserving FP tree algorithm, Cryptography technique, horizontal partitioned database, Secure Sum.

INTRODUCTION

Data mining techniques are available to retrieve useful information from large database. Prediction and description are the two fundamental goals of data mining. To full fill these goals many data mining techniques [1] [2] [3] [4] exists such as FP Tree Algorithm, Apriori algorithm [7] [8] [9], classification, clustering and so on. Among these, FP Tree Algorithm has wide applications to discover interesting relationship among attributes in large databases. FP tree algorithm is used to find the rules which satisfy the user specified minimum support and minimum confidence. In the process of finding FP Tree Algorithm, the set of frequent item sets are computed as the first step and then FP Tree Algorithm are generated based on these frequent item sets. Two types of database environments exist namely centralized and distributed. A Centralized database [4] [5] [6] [7] is a database located and maintained in one location, unlike a distributed database. One main advantage is that all data is located in one place. The disadvantage is that bottlenecks may occur. Many FP Tree Algorithm struggle with their management information systems and their membership databases. One of their primary struggles is the lack of centralized information. Too often, assns and nonprofits keep separate databases for membership, events, sales, and other processes. When at all feasible, these databases should be combined into a single, centralized database. There are several benefits to moving your data to a centralized system. Benefit in centralized database .data integrity, Valuable broad marketing information or history, Ease of training, Support. Distributed database [4] [5] [6] [7] is defined as collection of logically distributed database which are connected with each other through a network. A distributed database management system is used for managing distributed database. Each party has its own database and operating system. Charge in view of the motivation to have as a feature of privacy in data mining techniques to save from harm the confidential data of the user, there evolved an innovative stream in data mining period that is privacy preserving in data mining. There exists a key difference among regular data mining algorithms Under a variety of data mining techniques similar to classification, FP Tree Algorithm [6], clustering and privacy Preserving data mining algorithms that is the recognized algorithms deals with how to evaluate the Stored raw data and how to take out useful knowledge discovery patterns from the database Whereas in the afterward, it essentially deals with the sensitive information of the user records where privacy factor is the main concern and it is measured to be vital issue. The main aim in many scattered methods for privacy preserving data mining is to agree to useful aggregate computations on the complete data set through preserving the privacy of the individual parties’ data or information. Each party owner is interested to work together in obtaining combined results, but not fully trust other parties in conditions of the distribution of their own data sets. Several data mining system should satisfy the important property that is privacy preserving of data or information. Particularly in distributed data mining, privacy preserving is individual crucial feature. Secure multi party computation is a useful approach to save the privacy in distributed data mining. Privacy preserving data mining utilizes a mining algorithm to obtain mutually beneficial global data mining objectives without helpful private data. Therefore, in many data mining applications privacy preserving has become a significant subject.

II. SECURE MULTI PARTY COMMUNICATION

Approximately all Privacy Preserving data mining techniques rely on Secure multi party communication protocol. Secure multi party communication is defined as a computation protocol at the last part of which no party involved knows anything else except its own inputs the outcome, i.e. the view of each party during the execution can be effectively simulated by the input and output of the party. In the late 1980s [1], work on Secure multi party communication verified that an extensive class of functions can be computed securely under reasonable assumptions without involving a trusted third party. Secure multi party communication has commonly concentrated on two models of security. The semi-honest model assumes that every party follows the rule of the protocol, but is free to later use [2] [12] what it sees during execution of the protocol. The malicious model assumes that parties can arbitrarily cheat and such cheating will not compromise moreover security or the outcome, i.e. the results from the malicious party will be correct or the malicious party will be detected. Most of the Privacy Preserving data mining techniques assume an intermediate model, Preserving Privacy with non-colluding parties. A malicious party May dishonest the results, but will not be able to learn the private data of other parties without colluding with another party. This is a practical hypothesis in most cases.

III. PRIVACY IN FP TREE ALGORITHM USING CRYPTOGRAPHY BASED TECHNIQUE

Lots of algorithms suggested like Apriori algorithms [1] [8] [9] [13]. It is based upon the challenging monotone property. Due to their two main troubles i.e. frequent database examine and superior computational cost, there is a need of flattened data structure for mining frequent item sets, which moderates the multi scan trouble and improve the candidate item set generation. Tree shelf is an efficient algorithm based upon the lexicographic tree in which each node represents a frequent pattern [1] [6]. FP-Growth algorithm [6] is a restricted algorithm for producing the frequent item sets without production of candidate item sets. It is based upon divide and conquers approach. It needs database scan to discover all frequent item sets. This approach compresses the database of frequent item sets into frequent pattern tree recursively in the same order of magnitude as the sequence of frequent patterns. Then in next step divide the compressed database into set of conditional databases. Privacy preserving FP tree algorithm is very necessary because when the data is distributed among different partitioned like horizontal partition, vertical partition and mixed partition but in this we will describe only privacy preserving in horizontal partition. In case of horizontal partition the data is distributed in among different party so to find the global support, global confidence and life. Then privacy is play very important role to find global result, there are mainly three important method to provide privacy in horizontal partition are cryptography technique, heuristic based technique and reconstruction based technique but in this we mainly focus only on cryptography technique to provide privacy to horizontal partitioned data. And why the cryptography technique is more useful because two main reasons behind that.

1. It has a well recognized and well amorphous model meant for privacy which can essentially provide good number of methodologies for verifying and validating intention.

2. Cryptography branch has a broad mixture of tool set to incorporate privacy in data mining.

IV. TECHNIQUES OF PRIVACY PRESERVING FP TREE ALGORITHM IN HORIZONTAL PARTITION DATA WITHOUT TRUSTED PARTY

In horizontal partition data is distributed in among party the number of party will be grater then 2 (n>2). And no party is consider as a trusted party [10] all the party have their individual private data and no other party will able to know other party data .in this method basically we are using hash based secure sum technique .in secure sum each party will calculate their own data value and send to next party that near to original party and this will going till the original party will collect all the value of data after that the parent party will calculate the global support and global confidence and it also not necessary that the result that found is globally frequent or infrequent its depend on value which will found after collect all the value may be that globally frequent and may not be locally frequent to say that item is globally frequent its consider that item may or may not be locally frequent. Figure 1 shows that how the data is distributed in among different parties.

For this we are using one of method to find the global result of confidence and support. There are mainly number of steps to find the global confidence and global confidence.

Algorithm1

Step1: Each party will calculate their frequent item sets and Infrequent item sets and store the data value on memory.

Step2: Each party will generate their own random number because we are using hash based secure sum protocol so that each party have two random number one of its own and other is received by previous party.

Step3: Now the party 1 will calculate the partial support value by using the following formula. Ps j= Xj .support – Min support*|DB|-RN1-RNn where RN is random number.

After that party1 calculate the mask value

PSj = PSj + mask value

Step4: Party 2 compute the PSj for each item received the list using the formula

PSj= PSj + xj. Sup - min*support |DB| +Rn1-Rn (i-1)

Step5: After that the value of PSj calculated by party 2 send to next coming party and after that all the value is send to the original party and that original party will calculate all global support.

Step6: Party 1 will find whether that global support is grater then zero or not if the value is grater then zero then it will be global frequent otherwise is infrequent.

Step7: Like that the entire party will calculate the will calculate the global support party 3 party 4 party 5…….party n.

Step8: Finally the party 1 calculates the actual support by using the formula ASj = PSj + mask value

Step9: At last the party 1 will send the calculated value of actual support and global frequent item set to all other party in the horizontal partition.

Step10: Each party will generate the rule by using their confidence value.

Party 1 calculate the mask value by using the following formula

Mask value is calculated by using two different hash functions

Key1=Hash (key) =key mod N

And after that

Mask key = Hash2 (Key1) =Key+Mkey1

Double hash function is used to make the FP Tree

Algorithm rule more secure

Step1:-

TID List

T1 A1, A2

T2 A1, A2, A3

T3 A1, A2, A3, A4

Step2:-

A1:3, A2:3, A3: 2, A4:1

Step3:-Arranging in decreasing order

A1:3, A2:3, A3:2, A4:1

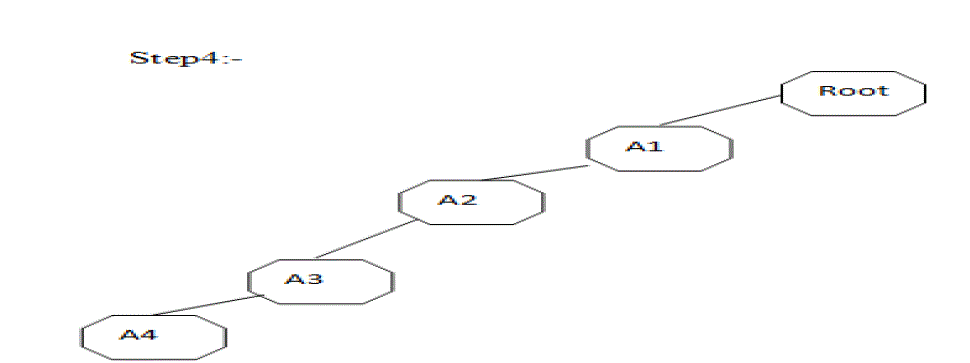Step5:- A1 :{( A1: 3)}

A2 :{( A1: 3)}

A3 :{( A2: 2, A1:2)}

A4 :{( A3: 1, A2:1, A1:1)}

Step6:- As here is minimum support is 40% so no candidate item set is selected

Step1:-

TID List

T1 A1, A3, A4, A5

T2 A2, A3

T3 A3, A4

T4 A1, A3, A5

Step2:-

A1:2, A2:1, A3: 4, A4:2, A5:2

Step3:-Arranging in decreasing order

A3:4, A1:2, A4:2, A5:2, A2:1

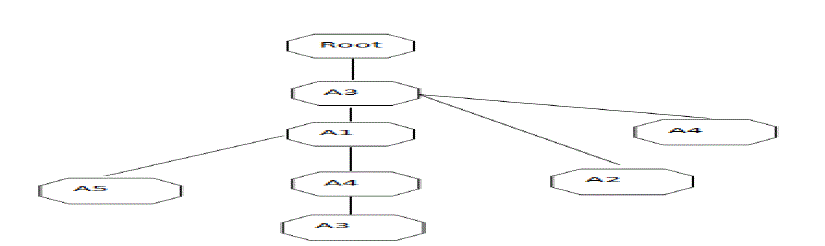Step5:- A1 :{( A3: 1)}

A2 :{( A3: 1)}

A3 :{( A3: 4)}

A4 :{( A1: 1, A3:1), (A3:1)}

A5 :{( A4:1, A1:1, A3:1) (A1:1, A3:1)}

Step6:- A4= (A3:2)

A5= (A1:2, A3:2)

Step7:- A4A3:2, A5A1:2, A5A3:2

Step8:- Support (A4A3) = Count (A4A3)/ Total number of transaction= 2/4=50%

Support (A5A1) = Count (A5A1)/ Total number of transaction= 2/4=50%

Support (A5A3) = Count (A5A3)/ Total number of transaction= 2/4=50%

The candidate item set is selected = {A1, A3, A4, A5}

Step1:

TID List

T1 A1, A2, A4

T2 A1, A2, A3

T3 A1

T4 A2, A4

Step2:-

A1:3, A2:3, A3:1, A4:2

Step3:-Arranging in decreasing order

A1:3, A2:3, A4:2, A3:1

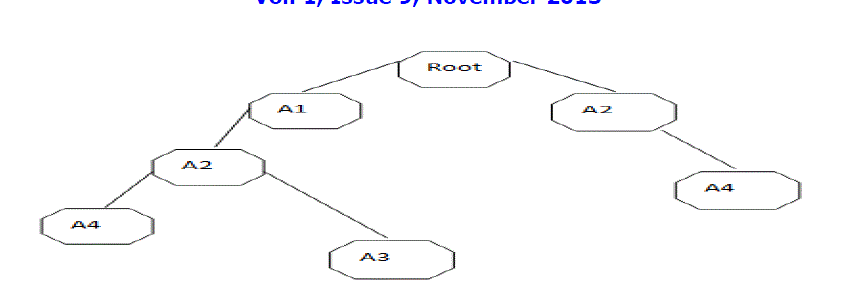Step5:- A1 :{( A1: 3)}

A2 :{( A1: 2) (A2:1)}

A3 :{( A2: 1, A1:1)}

A4 :{( A2: 1, A1:1), (A2:1)}

Step6: A4= (A2:2)

Step7:- A4A2:2

Step8:- Support (A4A2) = Count (A4A2)/ Total number of transaction= 2/4=50%

The candidate item set is selected = {A2, A4}

V. IMPLEMENTATION OF PRIVACY PRESERVING FP TREE ALGORITHM WITHOUT TRUSTED PARTY

At party 1: At party 1 no any candidate item is selected

At party 2: The list of frequent item at party 2 {A1, A3, A4, A5}

At party 3: The list of frequent item at party 3{A2, A4}

Consider the item set {A1}

Select the random number RN1=10, RN2=20, RN3=10

Key =110, M=2

Hash key=key mod M

Mask key=hash key- Mkey

Hash key=110 mod 2=0

Mask key=110-2^0=109

FOR FIRST ITEM SET I= {A1}

PS=I1Support- minimum support*DB+ (RNi-RNi-1) + Mask key

STEP1:

PS11= 3-.4*3+ (10-20) +109=100.8

PS12=2-.4*4+ (20-10) +100.8=111.2

ps13=3-.4*4+ (10-20) +111.2=102.6

Global encrypt support (GES) = partial support-mask key

GES= 102.6-110=-7.4

Actual support=global support+ database*minimum support

AS=-7.4+11*.4=-3

VI. TECHNIQUES OF PRIVACY PRESERVING FP TREE ALGORITHM IN HORIZONTAL PARTITION DATA WITH TRUSTED PARTY

In this method all the task will done by help of trusted party [11] and trusted party play important role in this method as well as trusted party is helpful of providing privacy to the database in among party and also data leakage is zero percent.

The following steps to calculate the FP Tree Algorithm in horizontal partition with the help of trusted party

Algorithm2

Step1: Trusted party will send a request to calculate the locally frequent item by the help of public key and hash function as well as minimum threshold support value.

Step2: After that each party will calculate the frequent item set and send to the trusted party without interfering of other party.

Step3: Trusted party will see all the frequent item set that coming from different party by help of private key and merged all frequent items set and remove all the duplicate item sets. For each party TP will generate the random number and sign (+ or -) and send to all the party that present to the database and that party is indicate weather that random number will added or subtracted its depend on the sign value.

Step4: Every party computes partial support for each item set in the merged list which is received from TP by using the formula

PS ij= Xj.sup – Min Sup × | D Bi | + (Sign i) RN i

Where i indicate the ith party, ranges from 1 to n and j indicates jth item set in the merged list, ranges from 1 to k. Each party then broadcast its computed PSij values for all the item sets in the merged list to all other parties. Step5: Every party computes Total PS ij for each item set Xj by using the formula.

Total PS ij = Σⁿ_i=1(PSIJ) for each j = 1 to k and sends to the Trusted party.

Step6: Trusted party will send the value of total partial support to all parties that present in database if any duplication will occur then the step 5 will follow again to calculate the partial support.

Step7: Trusted party computes Global Excess Support for each item set Xj by using the formula Global support j = TotalPS1j – Sign Sum RN

Where Sign Sum RN is computed by adding all the random numbers with their signs by trusted party. If the computed value of GES j ≥ 0 then the item set Xj is globally frequent otherwise it is globally infrequent.

Step8: For each global frequent item set Xj, Trusted party finds Actual Support as Actual support j = Global support j + Minimum Support * |DB|

Where |DB| = Σⁿ_i=1( |DBi| )

Step9: Trusted party will send the list of frequent item sets to all other parties present in distributed database.

Step10: Every party will generate FP Tree Algorithm by using the confidence to every parties and the minimum support that received by trusted party.

VII. IMPLEMENTATION OF PRIVACY PRESERVING FP TREE ALGORITHM WITH TRUSTED PARTY

For implementation we will take above database that contain of three different tables.

At party 1: At party 1 no any candidate item is selected

At party 2: The list of frequent item at party 2 {A1, A3, A4, A5}

At party 3: The list of frequent item at party 3 {A2, A4}

Consider the item set {A1}

Select the random number RN1=10, RN2=20, RN3=10

So that the size of database that contain |DB1|=3, |DB2|=4, |DB3|=4 so the size of global database is 11.

Trusted party will compute the signsumRN BY adding three random numbers

Signsum RN= (+) 10+ (+20) + (+) 10=40

Partial supports for A1 at different parties are computed as follows

At Party1

PS11=A1.Support-40%of DB1+ (Sign1) RN1

PS11=3-.4*3+ (+) 10=11.8

At Party2

PS21=A1.Support-40%of DB2+ (Sign2) RN2

PS21=2-.4*4+ (+) 20=20.4

At Party3

PS31=A1.Support-40%of DB3+ (Sign3) RN3

PS31=3-.4*4+ (+) 10=11.4

Party1 broadcast 11.8 to all other party party2 and party3, party2 broadcast 20.4 to party3 and party1, party3 broadcast 11.4 to party 1 and party2

Total PS11=PS11+ (PS21+PS31) =11.8+ (20.4+11.4) =43.6

Total PS11=PS21+ (PS11+PS31) =20.4+ (11.8+11.4) =43.6

Total PS11=PS31+ (PS21+PS11) = 11.4+ (20.4+11.8) =43.6

Trusted party receives 43.6 as total support of an item set A1 from three parties which ensures the computations performed by all others parties is correct. Trusted party when calculates the Global Excess Support by subtracting the SignsumRN from the TotalPS11

Global Excess support=TotalPS11-SignsumRN=43.6-40=3.6

The value of global support is 3.6 then it means that the item sets are globally infrequent.

Actual support of A1 is computed by adding minimum support of the total database of global excess support

AS11=Global Excess Support+ minimum support*|DB|=3.6+.4*11=8

Hence the Global frequent item A1 Support is 8.

Without trusted party having the global support is -3 and with trusted party having the global support is 8 so that the without trusted party is more faster and more secure as well the data leakage is zero but in the with trusted party is a ideal model so we need to provide the highest privacy and minimum data leakage to the database.

VIII. CONCLUSION

The difficulty of preserving privacy in FP tree algorithm when the database is distributed horizontally among n (n>2) number of parties when no trusted party is considered. A replica which adopts a hash based secure sum cryptography technique to find the global FP Tree Algorithm is propose in this paper by preserving the privacy constraints. Double hashing function is adopted to enhance the privacy further. The proposed replica capably finds global frequent item sets even when no party can be treated as trusted. And next in this paper we compare with trusted party. The trusted party initiates the process and prepares the merged list. All the parties computes the partial supports and total supports for all the item sets in the merged list using the sign based secure sum cryptography technique and based on these results finally trusted party finds global frequent item sets. And after comparing the result of these we find output that data leakage with trusted party is more as compare to without trusted party so privacy also without trusted party is more as compare to with trusted party.

Tables at a glance


Table 1	Table 2	Table 3

Figures at a glance


Figure 1	Figure 2

References

Agrawal, R., et al.: Mining association rules between sets of items in large database. In: Proc. of ACM SIGMOD’93, D.C, 1993,pp. 207-216ACM Press, Washington.
Agarwal, R., Imielinski, T., Swamy, A.: Mining Association Rules between Sets of Items in Large Databases. In Proceedings of the 1993 ACMSIGMOD International Conference on Management of Data, 1993, pp. 207-210.
Srikant, R., Agrawal, R.: Mining generalized association rules. In: VLDB’95,1994, pp.479-488 .
Agrawal, R., Srikant, R.: Privacy-Preserving Data Mining. In: proceedings of the 2000 ACM SIGMOD on management of data, 2000, pp. 439-450.
Lindell, Y., Pinkas, B.: Privacy preserving Data Mining. In: Proceedings of 20th Annual International Cryptology Conference (CRYPTO) 2000.
Kantarcioglu, M., Clifton, C.: Privacy-Preserving distributed mining of association rules on horizontally partitioned data. In IEEE Transactionson Knowledge and Data Engineering Journal, IEEE Press, Vol 16(9), 2004, pp.1026-1037.
Han, J. Kamber, M.:Data Mining Concepts and Techniques. Morgan Kaufmann, San Francisco, 2006.
Sheikh, R., Kumar, B., Mishra, D, K.: A Distributed k- Secure Sum Technique for Secure Multi-Site Computations. Journal of Computing, Vol2, 2010, pp.239-243.
Sugumar, Jayakumar, R., Rengarajan, C.:Design a Secure Multi Site Computation System for Privacy Preserving Data Mining. In InternationalJournal of Computer Science and Telecommunications, Vol 3, 2012, pp.101-105.
Muthu Lakshmi, N. V., Sandhya Rani, K.: Privacy Preserving Association Rule Mining without Trusted Site for Horizontal Partitioneddatabase. In International Journal of Data Mining & Knowledge Management Process (IJDKP) Vol.2, 2012, pp.17-29.
Muthulakshmi, N.V., Sandhya Rani, K.: Privacy Preserving Association Rule Mining in Horizontally Partitioned Databases UsingCryptography Techniques. In International Journal of Computer Science and Information Technologies( IJCSIT), Vol. 3 (1),2012 , PP. 3176 –3182.
Goldreich, O., Micali, S. &Wigerson, A.: How to play any mental game. In: Proceedings of the 19th Annual ACM Symposium on Theoryof Computing, pp.218-229.
Franklin, M., Galil, Z. & Yung, M.:An overview of Secured Distributed Computing. Technical Report CUCS- 00892, Department of ComputerScience, Columbia University.