ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
D.Elayarani1, R.Parijatham2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
Wireless multi hop networks, end-to-end (e2e) delay are a critical parameter for quality of service (QoS) guarantees. For the long flows, the end-to-end delay may grow quadratic ally with the number of hops. It is difficult to control the end-to-end delay of each flow. Proposed a new joint congestion control and scheduling algorithm for multi hop wireless networks. It contains fixed-route flows operated under a general interference model. The proposed system explicitly quantifies the tradeoff between throughput and delay of every flow. The proposed system introduces three techniques to reduce the congestion and to increase the throughput. They are window based flow control, virtual rate computation and finally the scheduling. The window based flow control controls the number of packets in the network. The packets to be sent are first injected in the window. The window injects each packet in the network only after receiving the acknowledgement for the previously sent packet. The scheduling is performed by the virtual rates computed by the virtual rate computation. The virtual rates are computed based on the flows in the node to be transmitted and then the capacity of the link. According to this scheduling.
Keywords |
||||||
| window flow control, rate based scheduling, congestion control, virtual rate computing, end to end and joint congestion control | ||||||
INTRODUCTION |
||||||
| Multi-hop wireless networks have been studied since the 70's. Several new applications of such networks have recently emerged. Community [9] wireless networks are multi-hop wireless networks that provide last-mile Access to peoples' homes [4]. This approach is an alternative to cable modem and DSL technologies. In large networks of sensors the scale and the environment are such that a multi-hop wireless network is the only feasible means of communication. A fundamental issue in multi-hop wireless networks is that performance degrades sharply as the number of hops traversed increases. For example, in a network of nodes with identical and Omni directional radio ranges, going from a single hop to hops halves the throughput of a flow because wireless interference dictates[6] that only one of the 2 hops can be active at a time. The performance challenges of multi-hop networks have long been recognized and have led to a lot of research on the medium access control (MAC), routing, and transport layers of the networking stack. Unlike wire line networks, where each link has a fixed capacity, the capacity of a wireless link varies with channel variations due to fading; changes in power allocation, link scheduling, or routing; and change[3]s in network topology, etc. These types of dependencies make the traditional layered design approaches less effective in the case of wireless networks and demand a new cross-layer design approach, which has spurred the recent interest in developing cross-layer[1] optimization algorithms for wireless networks. Motivated by the work of Kelly on fair resource allocation in wire line networks, researchers have incorporated congestion control and link scheduling into the cross-layer[12] optimization framework. The congestion control component determines the rates at which users inject data into the network so as to ensure that they fall within the capacity region of the network, and the scheduling[7] component decides which links should be active at what time and in what sequence to accommodate the rates allocated by the congestion control. A scheduling scheme is said to be throughput-optimal if it stabilizes the network for all rate vectors strictly within delta. A throughput-optimal scheduling scheme has been known, but it requires a centralized coordinator with high computational complexity, and is, in general, NP-Hard. Since distributed algorithms are highly preferred in ad hoc settings, a considerable amount of effort has been put forth in devising the simple distributed schemes that can achieve a certain fraction of the stability region[14]. One optimal solution is provided for the congestion control by the back pressure algorithm | ||||||
| There are two major issues on the delay-performance of the back-pressure algorithm. First, for long flows, the endto- end delay may grow quadratic ally with the number of hops[5]. Under the back-pressure algorithm, if a link schedules the long flow, the queue difference of the long flow must be larger than the queue length of the competing short flow. Therefore, when the joint congestion and scheduling algorithm converges, the queue length of the long flow at each hop must be around Hq, H (q-1).., and the total end-to-end backlog is of order O (H). By Little’s law, the end-to-end delay will also be of order O (H)[16]. Note that a packet needs at least time-slots to reach the destination. This implies that the backpressure algorithm may have significantly larger end-to-end delay for long flows. Second, under the back-pressure algorithm, it is difficult to control the end-to-end delay of each flow[10]. | ||||||
RELATED WORK |
||||||
| A wireless network which is modeled as a graph G = (¡;E) where ¡ is the set of nodes and E is the set of links. Let N and L be the number of nodes and links in the network, respectively [3]. We assume a time-slotted wireless system where packet arrivals and transmissions occur at the beginning of time slots of unit length. There are multiple Network flows in the network each of which corresponds to a particular source-destination pair. Arrival traffic is stored in input reservoirs and flow controllers are employed at source nodes to determine the amount of traffic to admit from input reservoirs into the network in each time slot [5]. Let nc be the source node and dc be the destination node of flow c. We will refer to the queue at the source node nc, which “stores” admitted traffic of flow c as an ingress buffer. It is worth emphasizing that we do not need physical buffers to implement these ingress queues in practice. Specifically, the backlog values of these ingress buffers can be simply maintained by software counters while all data packets are physically stored in the input reservoirs [17]. Each internal node maintains multiple finite buffers while ingress buffers at all source nodes are assumed to be unlimited [15]. This implies that the input reservoirs are unlimited in size because data packets at source nodes are physically stored in the input reservoirs. This assumption is justified by the fact that in many wireless networks buffer space is limited. | ||||||
| Under one-hop interference constraint, the interference Degree is at most[2]. Under the two-hop interference constraint, define the in-degree and out-degree of a node as the number of links in that ends in and originates from respectively. Define the directed degree of a link as the sum of the out-degree of transmitting node and in-degree of the receiving node [11]. The maximum directed link degree is the maximum directed degree of any link in. It has been shown that the value of can be upper-bounded. a new joint congestion control and scheduling algorithm that can guarantee a minimum throughput utilization close to of the system capacity, i.e., at most a factor of loss of throughput, and guarantee an upper bound on the per-flow end-to-end expected delay that increases linearly with the number of hops[14]. The congestion control algorithm is based on window based flow control, which deterministically bounds the main parameter to tune a joint congestion control and scheduling algorithm based on the back-pressure algorithm is the step size in the queue update. A larger step size may lead to smaller queue length [11]. However, a smaller step size is needed to ensure that the joint congestion control and scheduling algorithm converges to close-to-optimal system throughput. Although one may use the step sizes to tune the throughput–delay tradeoff, a change of the step size on one node will likely affect all flows passing through the node. Hence, it is difficult to tune the throughput–delay tradeoff on a per-flow basis[13]. | ||||||
JOINT CONGESTION CONTROL AND SCHEDULING ALGORITHM |
||||||
| A new class of joint congestion control and scheduling algorithms1 that can achieve both provable throughput and provable per-flow delay. Consider m flows in a multi-hop network operating under a general interference model with the interference degree of the interference degree will be given in Section and each flow m is given a fixed route with Hm hops [15]. Our algorithm consists of three main components: window-based flow control, virtual-rate computation, and scheduling. The main ideas of our algorithm to improve the end-to-end delay are as follows. First, by using window-based flow control, it can tightly control the number of packets inside the network. Second, by using a rate-based scheduling algorithm with the compute virtual rate as input to schedule packets, we do not need to wait for the packets to accumulate before making scheduling decisions [7]. A time-slotted wireless system, where packet transmissions occur within time slots of unit length. Let c? denote the capacity of link ?, which represents the number of packets that link ? can transmit in one time slot. We assume that c? is an integer for all link ?. We say two links interfere with each other, if they can not transmit data at the same time slot [6]. The set of all links that interfere with link ? is called the interference set of link ? and is denoted as E?. We adopt the convention that ? E?, i.e.,E? = {?} {?′ : ?′ E and ?′ interferes with ?}. Assume that the interference relationship is symmetric, i.e., if k E? then ?Ek. The interference degree of a link ? is the maximum number of links within its interference range that can be activated simultaneously without interfering with each other. | ||||||
| A. Window-based Flow Control Algorithm | ||||||
| The window-based flow control. For each flow, we maintain a window Wm at the source node, and we only inject new packets to the queue at the source node when the total number of packets for this flow inside the network is smaller than the window size [17]. This can be achieved by letting the destination node send an acknowledgement back to the source node whenever it receives a packet. There are two advantages for this approach. First, for each flow, we can tightly control the maximum number of packets in each intermediate node along the route [13]. The destination node to the source node at each time-slot. Through this feedback channel, the destination node can send the ACK to the source node, and the source node can then decide if it is possible to inject another packet at the next time-slot. Window based approaches reacts quickly reducing number of packets to be transferred to packet loss event | ||||||
| B.Virtual-Rate Computation | ||||||
| The virtual rate is computed at the source node which is the rates to inject the packet in the network. The virtual rates are calculated using the optimization problem formula. To find the virtual rate the Lagrange multiplier is used to solve the optimization problem[11]. The virtual rate is computed using the capacity of the link. It cannot directly use the virtual rate to inject the packets because it defines the rate at which the packets should be injected in the network. The virtual rate is used in the scheduling algorithm which is proposed. The scheduling algorithm performs the scheduling based on this virtual rate. In the virtual rate computation we use the Lagrange multiplier to produce the optimal virtual rates [15]. | ||||||
| Model the joint congestion control and scheduling | ||||||
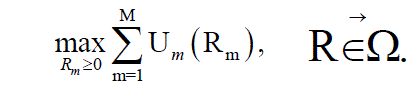 |
||||||
| The objective function of the dual problem | ||||||
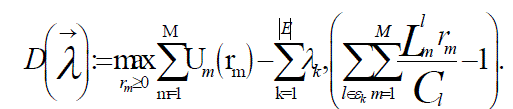 The following gradient algorithm to minimize D (delta) and compute the optimal virtual-rates The following gradient algorithm to minimize D (delta) and compute the optimal virtual-rates |
||||||
| Algorithm: | ||||||
| At each time: | ||||||
| The source node of flow m updates rm by equation | ||||||
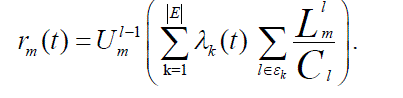 |
||||||
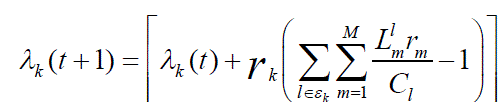 |
||||||
| Each link updates the dual variables by Equation | ||||||
| The variables are rm “virtual rates,” and they are not directly used to inject m flow packets Under our proposed algorithm. We choose not to directly use the virtual rates as the real injection rates due to the following reasons: first the rates are immediately passed to all links at the same time. In reality, a packet must traverse the links in a hop-by-hop fashion [10]. In order to control the end-to-end delay, an additional flow-control algorithm is needed to regulate this hop-by-hop packet flow. Second, the low-complexity virtual rate computation algorithm did not produce the schedule for link transmission [16]. We still need a scheduling algorithm to compute the schedule that can support the virtual rate vector. | ||||||
| C .Scheduling Algorithm | ||||||
| Rate based schemes on other hand has to wait for feedback before appropriate action can be taken thus continue sending at same rate .Each time-slot consists of an initial scheduling slot, which is further divided into F mini-slots. The links that are to be scheduled are selected in the scheduling slot, and the selected links transmit their packets in the rest of the time-slot | ||||||
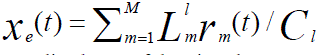 |
||||||
| Which is the normalized sum of the virtual rate over link, L and let: | ||||||
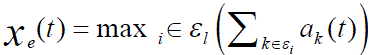 |
||||||
| Algorithm: At each time-slot: | ||||||
1. Each link first computes: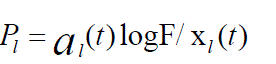 |
||||||
2. In the scheduling slot, each link then randomly picks a back off mini-slot (B) with distribution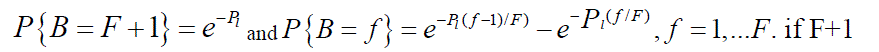 is picked by link, it will not attempt to transmit in this time-slot. is picked by link, it will not attempt to transmit in this time-slot. |
||||||
| 3. When the back off timer for a link expires in the scheduling slot, it begins [13] transmission unless it has already heard a transmission from one of its interfering links. If two or more links that interfere begin transmissions simultaneously, a collision occurs, and both transmissions fail. | ||||||
| 4. When a link begins transmission, it will randomly choose a passing flow m to serve with probability This algorithm can be easily improved by letting each link attempt only if it has packets to transmit, and if it starts transmission, it will randomly serve a flow m with positive [11] backlog with probability the number Of flow- packets at link at time. It is easy to see that this improved version will lead to higher throughput | ||||||
PERFORMANCE EVALUTIONc |
||||||
| The main steps of the analysis and the bounds on the throughput and delay of the above proposed scheme.[1][14]The virtual-rate computation algorithm has converged at time. Thus rm (t)=r*m, for the following time-slots. This implies that, for a particular flow, its service at every hop is identically and independently distributed across time[4]. This observation allows us to isolate flow m out of the network and view the flow as passing through a virtual tandem network of Hm queues. | ||||||
| The window size 2ci of each short flow is if the short flow passes link. The window size of the long flow is . The utility H log (.), function is for the long flow and for each short flow. Hence, when we increase the number of hops, the optimal rate assignment for the flows will be roughly the same. This will help us to observe how the average delay changes as the number of hops increases while the Throughput is relatively fixed[5]. The back-pressure algorithm with step size and to represent the shadow back-pressure algorithm with step size. For each scheduled link, one packet of the flow which achieves the maximum differential backlog is transmitted if the corresponding buffer has at least one packet waiting for transmission. a unified framework for joint rate. Control and scheduling in multihop wireless networks. Our solution to the joint rate control and scheduling problem has an attractive decomposition property. Using a dual approach. We show that the rate control problem and the scheduling problem can be decomposed and solved individually [5]. The two problems are then coupled by the implicit cost associated with each queue to solve the joint problem. We show via both analytical and numerical results that our joint rate control and scheduling algorithm can significantly reduce the queue length inside the network and improve the quality of service to the users. Congestion control schemes in general can be categorized into two groups based on the regulating parameter [7]. The first group includes those schemes that use a TCP-style congestion window at the sender or at the receiver(s) to control the load they provide to then network. Each transmitted packet decreases the number of available spots in the window by one, and each acknowledged increases that number by one. If at any time the number of available spots is zero, transmission is halted until at least one packet is acknowledged as received [8][9]. The size of the congestion window is increased if there is no congestion and is decreased with the detection of congestion. Using window-based congestion control in multicast applications proved to be more difficult than its use in unicast applications due to the difficulties that arise from the Ack implosion problem [7]. | ||||||
| The corresponding long-flow throughput is roughly the same as the BP algorithm, which is optimal. However, like the BP algorithm, the SBP algorithm requires centralized computation to achieve maximum capacity region. Furthermore, we observe that SBP requires roughly 7000 time-slots[16] for the whole algorithm to converge, and the total queue length inside the network. will first rise to a very large value as shown in contrast, the control variables under our algorithm will converge after around 200 time-slots as shown in Furthermore, because of window-based flow control, the total queue backlog of our algorithm is consistently the lowest at all time, even during the transient period. the average delay of the BP algorithm increases Quadratically with the number of hops, which is much larger than that of our algorithm. Note that our algorithm out performs the BP algorithm in the delay performance even though the BP algorithm utilizes centralized[13] computation. The simulation result shows that the average delay of SBP will be significantly larger in the transient phase. In contrast, the average delay of our algorithm does not deviate significantly from the theoretical value even in the transient period. Link scheduling must take into account the channel state. Specifically, let Φ0(_X (t))be the set of feasible schedules in time slot t where for each of these feasible schedules we only activate wireless links which are in the ON state[15]. this algorithm implement into the different techniques in the congestion control. | ||||||
CONCLUSION |
||||||
| Proposed a low-complexity and distributed algorithm for joint congestion control and scheduling in multi-hop wireless networks under a general interference model. Proposed algorithm is to control the congestion with window-based flow control and to use both virtual- rate information and queue information to perform scheduling. Proposed scheduling algorithm is fully distributed and only requires a constant time to compute a schedule. In the window based flow control the packets are first inserted in the window. Then each packet is inserted into the network only after receiving the acknowledgement for the previously sent packet in the network. So the number of packets in the network is reduced using this technique. Then the scheduling algorithm uses the virtual rates which reduces the delay in the flow. Each packet is inserted into the network only after receiving the acknowledgement for the previously sent packet in the network. So the number of packets in the network is reduced using technique for the future work the packets are sending via the dynamic routing. The congestion and the scheduling is performed using this virtual rate for the dynamic routing. | ||||||
Figures at a glance |
||||||
|
||||||
References |
||||||
|