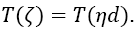Ablative Pressure Pulse

Abstract

We examine herein a simple model for the evolution in time of the pressure which a suddenly vaporized, ablating layer exerts upon the subjacent body. The model invokes a plausible construct of surface material instantaneously thrust into a gaseous regime governed by a Maxwell-Boltzmann phase space distribution. The surface pressure per se is gotten by computing the time rate of change of the momentum per unit area which the retrograde molecules, and only those, transfer through impact/reflection to the unvaporized body below. An explicit pressure formula, one alluding to the variable gas temperature within the vaporized layer, is obtained as a single quadrature requiring numerical integration at finite times τ>0 past the onset of impact. Limiting, null pressure values, both close-in, with τ=0+, and in pulse aftermath as τ→∞, can nevertheless be extracted in analytic terms, confirming in particular the indispensable asymptotic evanescence. A universal formula in dimensionless variables is given for pressure versus time, both suitably normalized.

Keywords

Maxwell-Boltzmann velocity distribution; Time-of-flight arrival delay; Heaviside unit step function; Dirac delta function; Momentum transfer in non-dissipative elastic recoil; Pulse pressure profile reduced to a single quadrature; Dimensionless pulse pressure formulae

Introduction

While nuclear exchanges in space or elsewhere seem less likely than they were during the Cold War of recent memory, threatening possibilities of exoatmospheric blasts nevertheless do persist. Any such blast would inflict, short of total destruction, a surface vaporization of space vehicles in its proximity. The vaporized atoms, as part of their recoil against the subjacent, be it solid or liquid skin layer, would exert upon the space vehicle a pressure pulse capable of deflecting it from its intended trajectory.

We seek here to abstract from this scenario an idealized model wherein an infinite sheet of solid material has a thin layer instantaneously vaporized as a consequence of, say, an intense x-ray impact. The temperature of the vaporized gas is by having the local energy deposition, minus the heat of vaporization, distributed through a 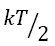equipartition among all available modes, that local gas being Maxwell-Boltzmann distributed thereafter in velocity space. Gas molecules already directed outward contribute nothing to surface pressure, whereas those with inward velocity components reflect from the solid or liquid interface and thus impart to it a perpendicular component of momentum whose rate of change is experienced as a surface pressure pulse. Set out below is our attempt to follow the time history of this pulse.

Description

We measure co-ordinate x in centimeters, perpendicularly inward from the surface about to undergo ablation. An impulse of energy I (ergs per square centimeter) is incident along the normal from the exterior at time τ=0 sec, and penetrates instantaneously while shedding strength in accordance with Ie^-αx real positive α being an attenuation constant (inverse centimeters) characteristic of surface composition and the nature of the impinging energy. Accompanying pulse decay is a continuous, local deposition of energy into the surrounding material in an amount αle^-ax(ergs per cubic centimeter).

We imagine the surface material to be vaporized down to a depth d, past which there ensues a transition layer bridging a melted, boiling phase into a solid regime. The vaporized material, with n particles per unit volume and f degrees of freedom per molecule, regardless of whether these degrees pertain to external dynamic or internal energies, is conceived to exhibit a temperature profile T(x) (degrees kelvin) given by

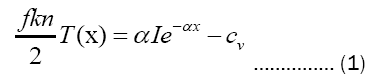
wherein is c_v the heat of vaporization per unit volume and we evidently must have αI>c_v . At the boiling depth d we require that

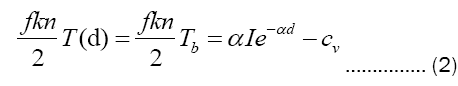
with T_b , known a priori, being the vapor temperature in equilibrium with the boiling melt beyond.¹Moreover, at all preceding points 0≤x≤d the vaporized material is assumed to undergo an instantaneous entry into a local Maxwell-Boltzmann (MB) phase space distribution

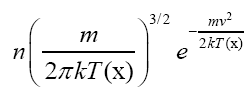
with k=1.38064852 × 10⁻¹⁶ erg/°K and m the individual molecular mass.

Molecular momentum transfer at vaporization/melting depth d

We consider an infinitesimal area dA upon the vapor/melt interface and adopt polar co-ordinates (ρφ) centered at some point therein. Area element dA subtends a solid angle 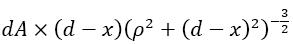at any point in the vapor overlay, and it is only the vapor particles having velocity directions within that angle which are capable of impinging upondA following the 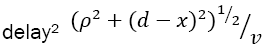On impact/rebound they each transfer a perpendicular component of momentum in an amount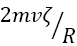, it being assumed, simplistically to be sure, that elastic surface collisions prevail. And so, with the MB distribution in mind, we find that infinitesimal area dA absorbs in time τ≥0 a perpendicular momentum dP(τ) in an amount.

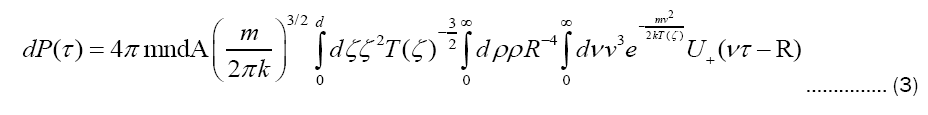
with U₊(vτ-R) being the Heaviside unit step, unity when vτ >R and zero otherwise, and 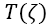replacing T(x) in the obvious way (consult Endnote 2). Differentiation wrt τ brings in the Dirac delta function δ and provides the interface ablative pressure p(τ) in the form

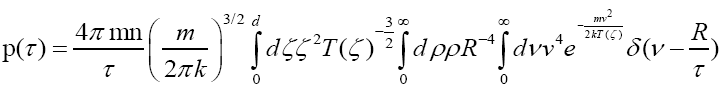
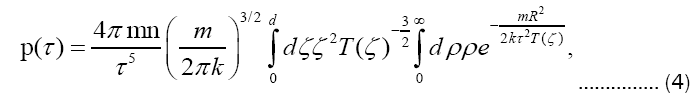
the integration over velocity v yielding easily in the presence of Dirac’s delta. Furthermore,

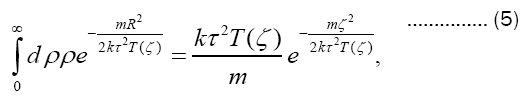
which demotes the right-hand side of (4) into just a single quadrature,

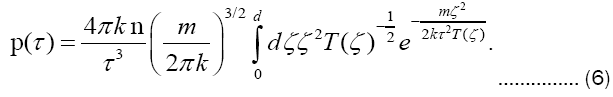
Limiting evaluations

At all finite times τ and with realistic parameters in hand, outright numerical integration is required to extract pressure estimates from (6). This obstacle notwithstanding, some semi-quantitative statements can be made at the limiting extremes

τ ↓0+and τ → ∞:

To begin with, as τ → ∞, evident by inspection that p(τ) properly descends to zero as the inverse cube power τ^-3

Likewise null close to the time origin are p(0+) from (6) and its slope

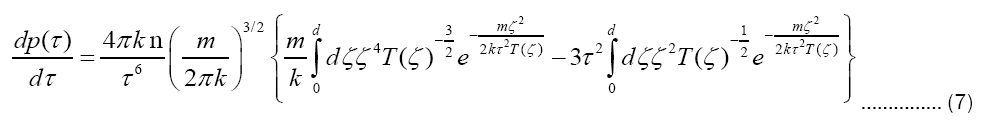
since, whenever l’Hôpital’s rule gives

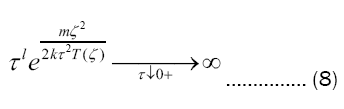
for all three powers l = 3, 4, and 6 now in play. Thus

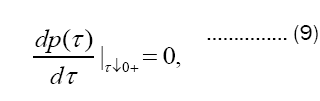
which, in conjunction with p(0+)=0, bespeaks an exceedingly gradual pressure growth past the moment of impact.

On the other hand, glancing somewhat further ahead, we find the time τ_pp of peak pressure by setting

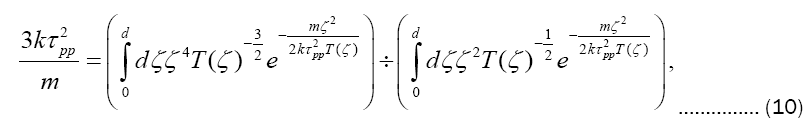
or else

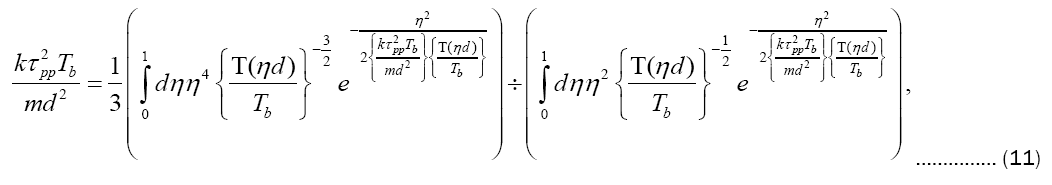
and then solving numerically for the dimensionless variable 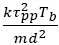The existence of τ_pp is guaranteed by virtue of the fact that (6) presents the pressure p(τ) as a product of factors, one of which τ⁻³ clearly falls with growth in τ, whereas the other equally clearly rises.

Universal pressure profile

In a similar vein, prior to numerical implementation, we recast (6) in terms of a dimensionless time

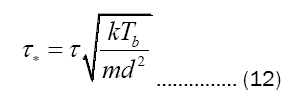
and temperature

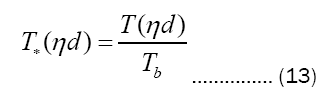
so as to obtain

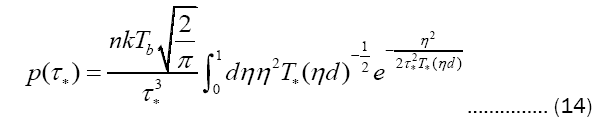
with

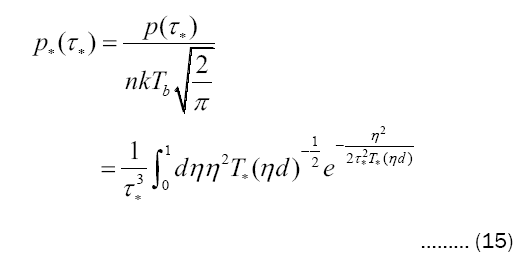
as a similarly dimensionless pressure. In view of Equations (1) and (2) we further have

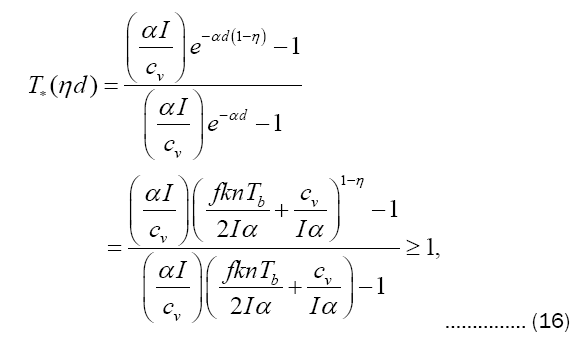
which latter reveals the second line of (15) in its universal aspect of depending only upon dimensionless parameter groupings.

A numerical example

We have carried out computations based on Equations (15) and (16) roughly tailored for aluminum. Accepted values gleaned from the open literature are

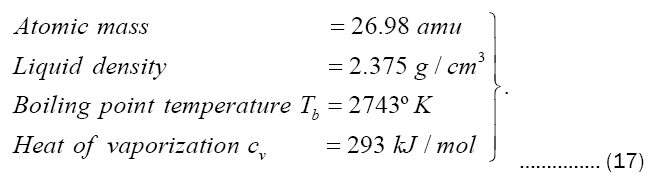
With use of Avogadro’s number N = 6.02214 × 10²³ atoms/mol we proceed to find the boiling substrate number density

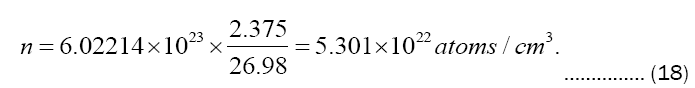
Setting f=3 so as to account for purely translatory freedom and with Boltzmann’s constant with k=1.38064852 × 10⁻¹⁶ erg/°K, we get

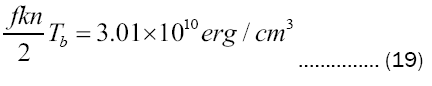
whereas

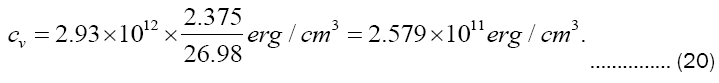
If we regard 50 keV as a typical x-ray photon energy then, from an online, public access x-ray attenuation calculator [1] we find

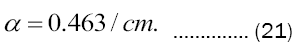
We next turn the matter on its head by insisting upon a vaporized depth d of just one cm and solving

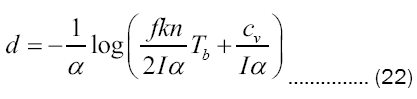
for the energy inflow

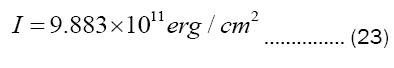
adequate to achieve this, a value that lies comfortably within the range of nuclear blast intensities [2].

And finally, with the toolkit of values thus assembled, we find, via Gaussian integration of (15), the ablative pressure temporal profile depicted in Figure 1. Furthermore, with the scaling factors from (12) and the first line of (15), respectively for time

Figure 1: Normalized pressure profile p_*(τ_*)vs normalized time τ_*

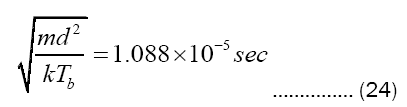
and pressure

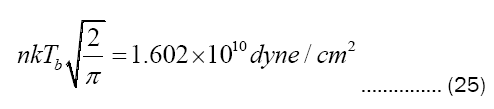
kept firmly in mind, this pressure pulse would seem to indicate convincingly that the ablating surface experiences a substantial jolt, easily able to deflect from its intended course the subsequent trajectory of an exposed space vehicle. The cumulative impulse

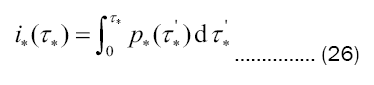
is tracked in Figure 2, once more in dimensionless terms. Its scale is given by

Figure 2: Normalized impulse profile i_*(τ_*)vs normalized time τ_*

Endnotes

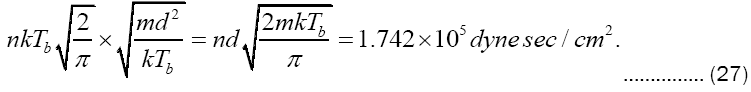
1. Under the present circumstances, a resolute optimism is required to even think, let alone to write about thermodynamic equilibrium, including our foundational allusion to the Maxwell-Boltzmann distribution law. Otherwise put, we are committed here to the assumption that the granularity of our temporal perception is far, far coarser than any operative thermalization times. Observe in passing that (2) gives the vaporized depth

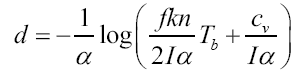
quite explicitly, with an implied insistence that 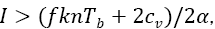an inequality stronger even than that mentioned in connection with Eq. (1) and designed to accommodate a positive depth d to the prescribed value of melting temperature T_b.

2. For ease of writing we set henceforth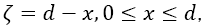 for the distance upward from the vaporized/unvaporized interface, and 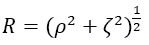for the molecular flight interval. We then proceed to abuse notation by writing 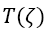for ��(x) as that latter appears on the right in Eq. (1). Such notational abuse still further intensifies in (11) et seq., when scaling by depth d leads us to write

References

1. Günter Weber, Helmholtz-Institut Jena, Fröbelstieg 3, 07743 Jena, Germany.
2. Glasstone S., et al., The effects of nuclear weapons, Third Edition, United States Department of Defense and the United States Department of Energy, 1977:305-310, 355-357.