Keywords
|
| Gaussian pyramid, Scale Invariant Feature Transformation, keypoints, Spatio-Temporal domain. |
INTRODUCTION
|
| Human action recognition these days is the developing area in the computer vision. The aim of the human action recognition is to recognize the action performed in a video automatically thus reducing the need for human interaction. Many algorithms have been used till date for the human action recognition. |
| In the initial set of algorithms blob based, holistic and part-based representations methods were used for recognition. But however they failed to produce accurate results under different variations. This led to a need for an efficient algorithm which would produce accurate results even under such variations. The bag of features model provided scale and location invariance [1].They did not provide rotation invariance. Lowe came up with the SIFT algorithm which provides scale, location and rotation invariance in the year 1999[2]. |
| The 2D SIFT algorithm initially introduced considered images as input. The scale space and the Gaussian pyramid were formed and the interest points were found from the DoG images. These interest points were further used recognition. But this algorithm provided invariance only in the spatial domain and neglected the temporal domain. Dollar et al in the year 2005 gave importance to only the temporal domain discarding the spatial constraints [3]. Since they relaxed the spatial constraints, their detector detects more interest points than a 3D Harris detector by applying Gabor filters on the temporal dimension to detect periodic frequency components [4]. |
| In this paper a ST-SIFT detector algorithm is introduced, were equal importance is given to both spatial and temporal domains. The key points are found in xy, xt and yt domain individually and then the common points which contain the vital information are selected. The ST-SIFT detector algorithm would be further enhanced to ST-SIFT algorithm which makes the algorithm not only scale and intensity invariant but also rotation invariant. SIFT algorithm has its applications in many fields such as medical analysis, real time applications, traffic monitoring, sports event analysis, human-computer interface, video surveillance etc. |
| The materials used for this work are: |
| - The videos from Google are taken as the database. |
| - The software used in the project is MATLAB |
METHODOLOGY
|
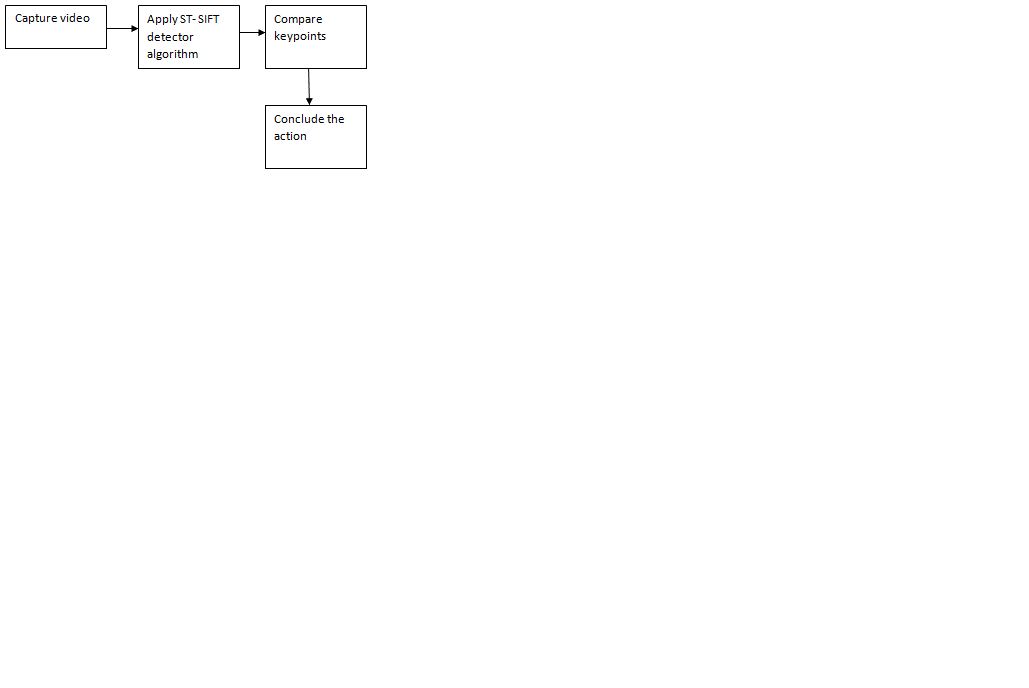
| The Fig. 1 shows the block diagram of the human action recognition using ST-SIFT algorithm |
| Initially the video containing the human actions is obtained. It is divided into frames which are then input to the STSIFT detector algorithm for further processing. The keypoints are compared with those in the database and the action performed is concluded. |
ST-SIFT DETECTOR ALGORITHM
|
| The Fig. 2 shows the block diagram of the ST-SIFT detector algorithm |
| A. Finding Gaussian operator |
| The Spatio Temporal Gaussian operator is found using the spatial and temporal scale parameter sigma and tow. The operator is found at different scales which are required to construct the scale and the time space. |
| B. Constructing a scale and time space |
| The initial phase of the algorithm involves progressive blurring of the original video frames with Gaussian operator which results in first octave. The original video frames are then resized to half its size and blurred out video frames are obtained which result in the second octave. Every consecutive octave will have its size reduced by half of its preceding octave. The number of octaves and scales are determined based on the characteristics of the video. |
| C. Construction of DoG pyramid. |
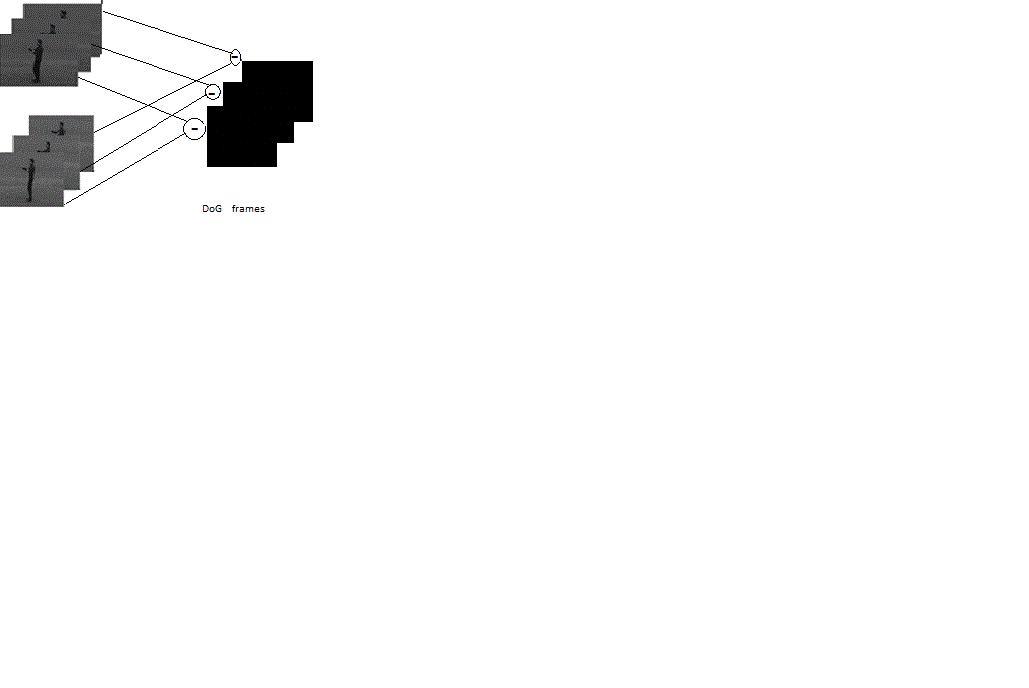
| The difference between neighbouring set of frames differing only in scale and time factor are found. The resulting video frames represent stable locations in scale and time space. These video frames are called the DoG frames. The problems rose due to the scale and temporal variations are overcome by using these DoG frames for further processing. As a result a specific action in different scales will be recognized the same action. These frames can then be used in further steps to obtain the key points. |
| D. Finding keypoints |
| The local maxima and the minima i.e. the key points have to be found. They are found by iterating through each pixel and checking its neighbours. If the pixel being checked has its value greater than the maximum (lesser than the minimum) value of the neighboring pixels, then it is considered the key point. Initially keypoints in xy, xt and yt planes are found individually. The common key points in all three planes contain important and useful information. These points are extracted and further considered the keypoints. The red dot in the Fig. 3 represents the pixel being compared. There are totally 26 neighboring pixels, 8 of them in the same frame, 9 in the frame-1 and 9 in the frame+1.If the pixel has the value more than or less than all the other 26 pixels then it will be taken as the keypoint. |
| The Fig. 3 shows finding keypoints only in xy plane for a single pixel. Similarly keypoints are found in yt and xt planes. This process would be continued for all the pixels in the frames to obtain the final set of keypoints. |
| E. Get rid of bad key points |
| Few of the key points obtained might be due to noise and few do not contain important information. The algorithm becomes more efficient and robust if these bad points are eliminated. Therefore a threshold is set and any key point having pixel value below this threshold is no more considered a key point. The key points if any at the edges are also eliminated. |
| F. Action recognition |
| The keypoints for a video involving human action are found. For a different video captured under different conditions involving same action being performed, keypoints are again found and are compared. If they match each other, it indicates that both the videos contain the same action being performed. |
EXPERIMENTAL RESULTS
|
| The time scale space for the capture video was found which is shown in the Fig. 4. Along the horizontal axis the octaves are marked as octave 1 and octave 2. The top most set of frames in first octave represents the original set of frames. As we come down along the vertical axis from top to bottom we observe the variation in the scale of the frames. These are the frames blurred out with different scaling factor using the ST-Gaussian operator. The number of scales depends on the video and the efficiency of the results required. More number of scales results more efficiency and accurate results. The second set of frames in the Fig. 4 (2nd column) are obtained by resizing the original video to half its size by leaving out every alternate pixel in the each frame and every alternate frame in the video. If more number of octaves is required the process of resizing continues. |
| The Fig. 5 shows how the single set of DoG frames were found from the time scale space. |
| The keypoints were found from the DoG frames. |
SUMMARY AND CONCLUSIONS
|
| In this paper ST-SIFT detector which is the extension to the spatial SIFT detector algorithm was demonstrated. The purpose of this extension was to obtain more efficient scale and intensity invariant features in both spatial and temporal domain. A single video of human action at different scales and intensities were used for demonstration. |
Figures at a glance
|
 |
 |
 |
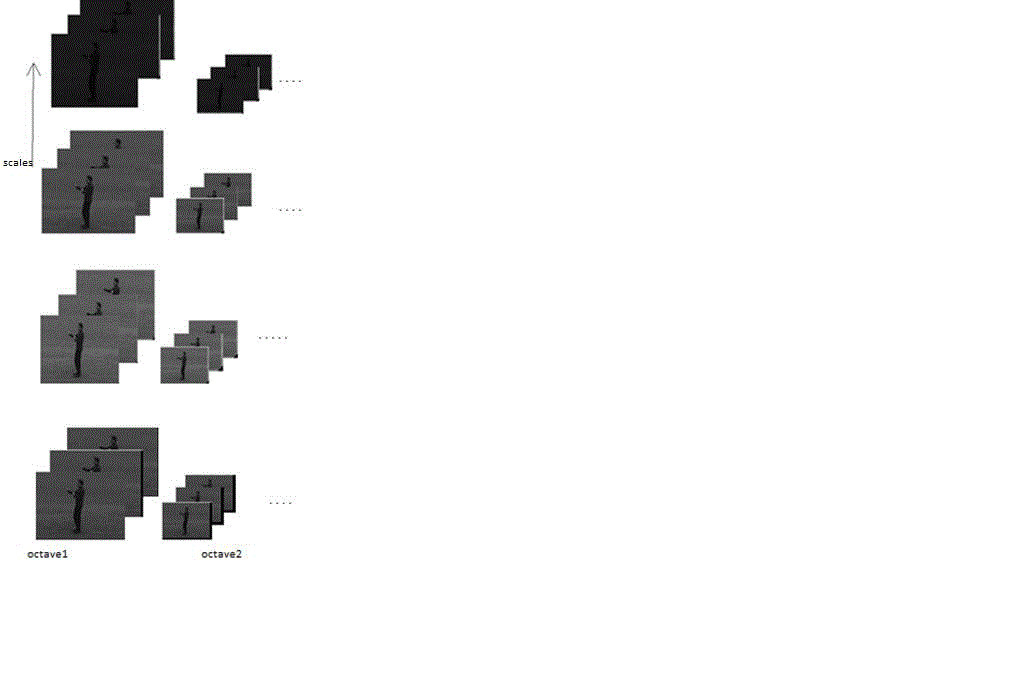 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
|
| |
References
|
- Niebles, J, Wang, H and Fei-Fei L ( 2008), ” Unsupervised learning of human action categories using spatial-temporal words”,
- International Journal of Computer Vision, Vol.79, pp.299-318.
- Lowe David G (1999) ,"Object recognition from local scale-invariant features", Proceedings of the International Conference on Computer
- Vision, Vol.2, pp.1150–1157.
- Dollar P, Rabaud V, Cottrell G and Belongie S (2005), “Behavior recognition via sparse spatio-temporal features”, IEEE International
- Workshop on Visual Surveillance and Performance Evaluation of Tracking and Surveillance, Vol.2, pp.65-72.
- 4. Chen Ming-Yu and Hauptmann Alexander, "MoSIFT: Recognizing Human Actions in Surveillance Videos" (2009). Computer Science
- Department, Paper 929, 2009, http://repository.cmu.edu/compsci/929, retrieved on 12/1/2014.
|