Keywords
|
| Tapped delay line filter, Adaptive Synchronization, Time varying channel, Adaptive Filtering |
INTRODUCTION
|
| From last few decades adaptive filtering is gaining momentum in many Digital signal processing (DSP) applications. Digital signal processing (DSP) has been a major player in the current technical advancements such as noise filtering, system identification, and voice prediction. In recent times the Kalman adaptive filter algorithm has been used for solving these optimization problems to more traditional methods such as steepest descent. The benefits of Kalman filtering for parameter estimation when neural networks are the approximating functions. |
| Adaptive synchronization is an important part in coherent communication systems, especially for those employing a high bandwidth-efficient modulation scheme such as quadrature amplitude modulation (QAM) [3]-[4]. Adaptive synchronization important in conventional single-carrier communication systems, but also is necessary in multicarrier communication systems [1]. The Kalman filter is known as the optimally recursive linear filter in the minimum mean squared error (MMSE) sense [5]. The phase and observations can be linear in the measurement equation and thus the Kalman filter is applied. |
| The Kalman filter is used to estimate of the state variable given an a priori estimate and observed measurements. Kalman filter equations represent the least squares problem and are solved by evaluating cross- covariances and autocovariances between estimated state variables and observations. As the covariance is an optimal measure only for linear dependence, the Kalman filter is an optimal, unbiased estimator for linear models of multivariate Gaussian. Non- Gaussian marginal functions or multivariate dependence structures can originate from strong non-linear model behaviour and compromise the results of the filter. |
| This paper is organized as follows: In section II linear channel estimation is explained. Then parameter estimation, state estimation and linear channel estimation is explained. In Section III, Kalman filter is explained using tapped delay line channel model with Kalman parameter equations. In Section IV, shows the true values of weight, estimated tap weight, Kalman gain and minimum mean square error (MMSE). Finally, a conclusion is made. |
LINEAR CHANNAL ESTIMATION
|
| The term estimator is related to the filtering. It is used to refer as a system i.e. designed to extract information about a prescribed quantity of interest from noisy data. The term channel estimation allows the receiver to approximate the effect of the channel on the signal. The channel is suffered from the two impairments: ISI and Noise [9]. The ISI (inter symbol interference) and noise etc. are remove by using channel estimation. The net result of two impairments is that the signal received at channel output is a noisy and distorted version of the signal that is transmitted. The function of the receiver is to operate on the received signal and deliver a reliable signal to a user at the output of the system. |
| A. Parameter Estimation |
| In the parameter estimation parameter does not change at all or changes slowly in time, whereas the state estimation continuously evolves in time. Parameter identification in many communication and control system some of the system parameters are not known with desired accuracy. The method of estimating these known parameter from observed data is called parameter identification. System identification the more general problem of developing a mathematical model of the system from observed data is called system identification[6]. |
| B. State Estimation |
| State estimation is described by signal processing, filtering and smoothing. Three basic approaches used for estimation are least-squares, maximum-likelihood, and Bayesian. An estimator is defined as a function of the observations possessing certain desirable properties such as unbiasedness, consistency, and minimum variance. A Kalman filter provides estimates that are optimal in the least-squares, maximum-likelihood and Bayesian sense for a Gauss-Markov model. The stochastic process is Markov if, given its present state, its future is independent of its past[7][8]. |
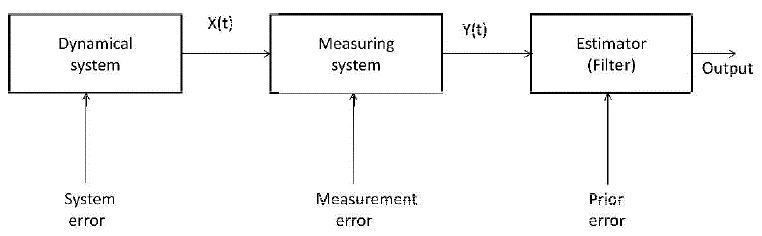
| A continuous time dynamical system whose state at time t is denoted by the multidimensional vector x(t). The equation described the evolution of the state x(t) is usually subject to system errors. The filtering problem is complicated by the fact that x(t) is hidden and the only way it can be observed is through indirectly measurement whose equations is a function of the state x(t) itself. Moreover the measurement equation is subjected to unavoidable noise of its own. The dynamical system is given in below fig. 1. |
| C. Channel Estimation |
| The Channel estimation is defined as the process which characterizing the effect of the physical channel on the input sequence. The channel estimate, estimates of the impulse response of the system, if the channel assumed to be linear. It must be stressed once more that channel estimation is only a mathematical representation of what is truly happening. A good channel estimate is one where some sort of error minimization criteria is satisfied (e.g. Minimum Mean Square Error (MMSE) [12]. |
| There are two channel estimation methods are proposed. The Maximum Likelihood (ML) estimator is unbiased, but it is more sensitive to noise. The second channel estimation method, based on the minimization of the mean square error (MMSE) [9].The signal received from the channel is suffer from phase-distortion, inter symbol interference and thermal noise. |
| There are various reasons to estimate the channel that is it allows the receiver to calculate the effect of the channel on the signal, remove inter symbol interference, noise. In Diversity techniques Rake receiver use the channel estimation to implement the match filter such that the receiver is optimally matched to the received signal instead of the transmitted one. Minimize the error probability maximum detectors used channel estimation technique. It also allows the implementation of the coherent demodulation. Coherent de-modulation requires the knowledge of the phase of signal. |
KALMAN FILTER
|
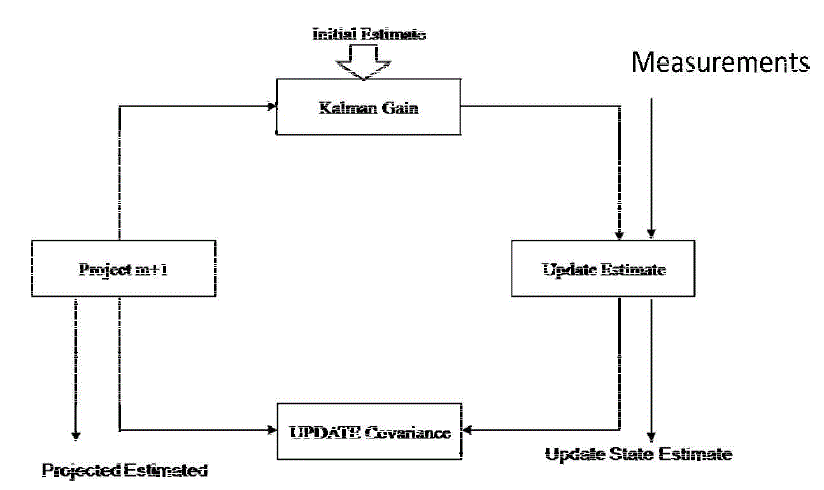
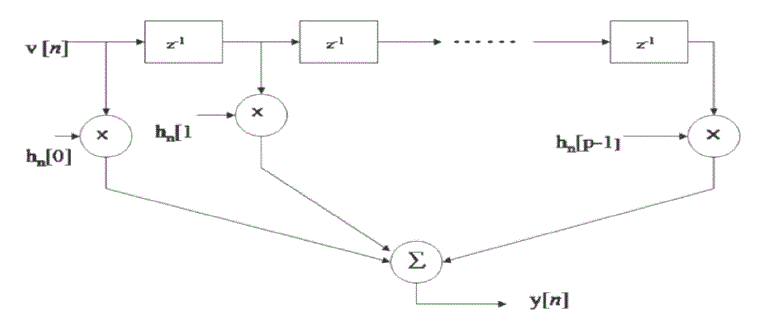
| The Kalman filter is a set of mathematical equations that provides an efficient computational (recursive) means to estimate the state of a process, in a way that minimizes the mean of the squared error. The Kalman filter is an efficient recursive filter which estimates the state of a dynamic system and noisy measurements. The Kalman filter is widely used in navigational and guidance systems, radar tracking, sonar ranging, and satellite orbit determination, as well as in fields as diverse as seismic data processing, nuclear power plant instrumentation, and econometrics. The signal is characterized by a dynamics or state model where the kalman filter may be thought of a sequential MMSE estimator of a signal that contains noise. It generalizes the sequential MMSE estimator, to allow the unknown parameters to evolve in time according to a dynamic model. Fig. 2 shows the block diagram of kalman filter as estimator. Fig. 3 shows the Tapped delay line linear channel modal. |
| Kalman filter parameter equation are given as |
| 1. Prediction: |
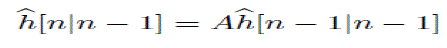 .....(1) .....(1) |
| 2. Minimum Prediction MSE: |
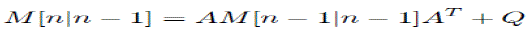 ......(2) ......(2) |
| 3. Kalman Gain: |
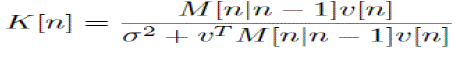 ........(3) ........(3) |
| 4. Correction: |
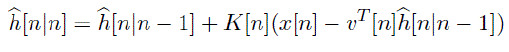 .......(4) .......(4) |
| 5. Minimum MSE: |
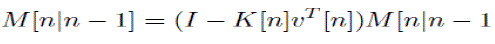 ......(5) ......(5) |
| Initializations: |
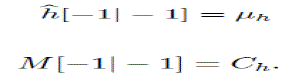 |
RESULT AND DISCUSSION
|
| The parameters of the channel are estimated by using kalman filter. The channel is assumed to be time varying in nature. The channel is act as a tapped delay line modelled with n no of weights. The no. of tap weights is assumed as per requirement. Matlab simulation results of time varying channel estimation using kalman filter. |
| We implemented the Kalman filter estimator for a tapped delay line having p = 3 weights |
| using MATLAB version 7.6.0(R2008a).We assumed |
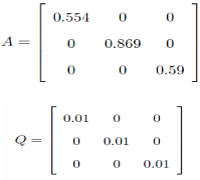 |
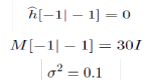 |
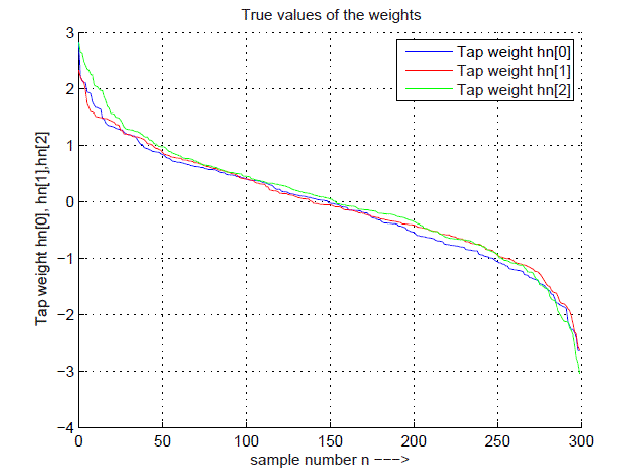
| The true values of the weights are shown in fig 4. There are three tap weights hn[0]; hn[1] and hn[2]. The no. of tap weights may be increases. The graph shows that the values of true weights are decreases monotonically. The graph can be drawn for n no. of samples. The value of sample may be fixed or it can be vary as per requirement. |
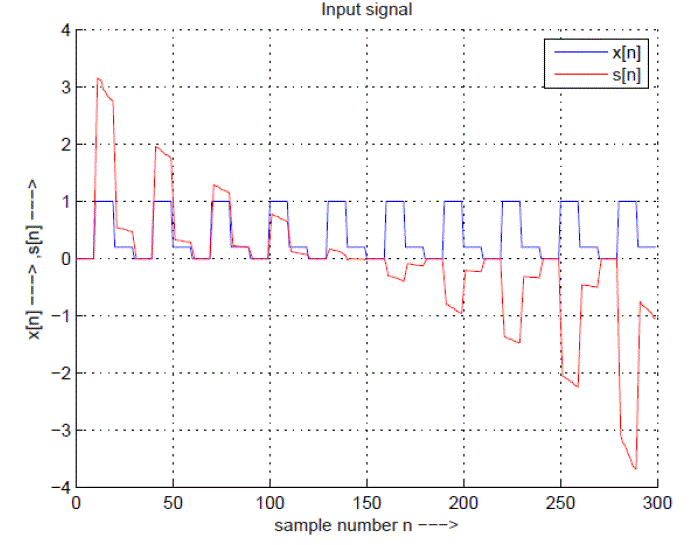
| Input signals are shown in Fig 5. X[n] is the desired input and S[n] is the actual output which is obtained. The s[n] is the noiseless signal. The desired input signal is suffer from inter symbol interference and noise. And s[n] output signal obtain without noise. |
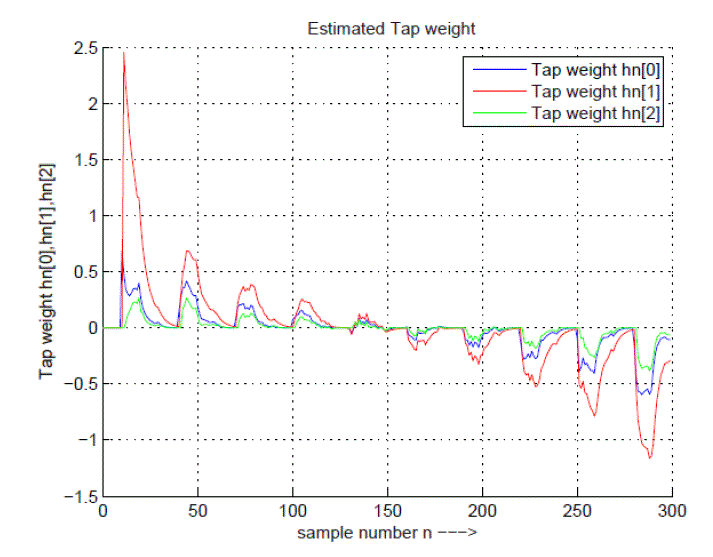
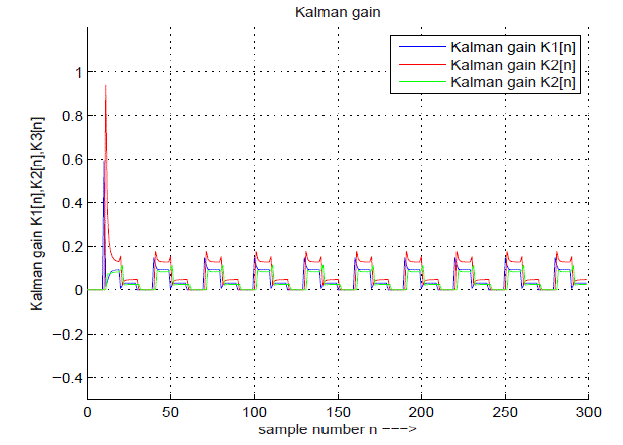
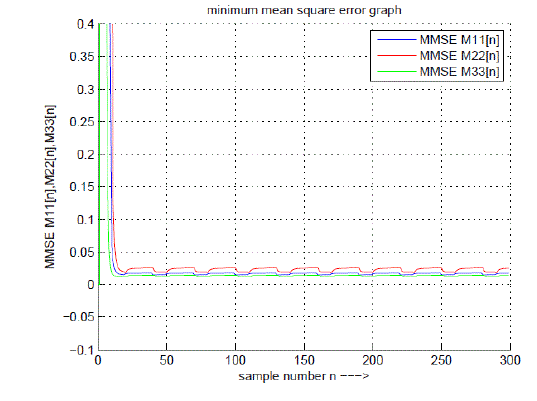
| The estimated tap weights are shown in Fig 6. Then the actual values of the tap weights are estimated by applying kalman parameters. The three estimated tap weights value are considered hn[0]; hn[1]; and hn[2]. The calculated Kalman gain is shown in the Fig. 7. It indicates that as the no. of tap weight increase Kalman gain decreases as per graph. The minimum mean square error is shown in Fig 8. This MMSE graph indicates the as no tap weights are increases the error is minimized as per graph. To minimize the error the gain is also decrease |
CONCLUSION
|
| In this paper, channel parameters are estimated and Adaptive Synchronization is done by using Kalman filter. The channel is assumed to be time varying in nature is modelled as a Low Pass tapped delay line filter. Tapped delay line linear channel model is used to estimate the parameter of the channel using Kalman filter. |
| |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
Figure 8 |
|
| |
References
|
- C. H. Huang, S. C. Chen, and D. C. Chang, “A study on joint effect of synchronization and channel estimation in the DVB-T receiver,” in 2005 8th International Symposium on Communications (ISCOM 2005), Kaoshiung, Taiwan, Nov. 2005.
- D. R. Stephens, Phase-locked Loops for Wireless Communications: Digital, Analog and Optical Implementations, Kluwer Academic Publishers, 2nd ed., 2002.
- L. K. Tan et al., “A 70-Mb/s variable-rate 1024-QAM cable receiver IC with integrated 10-b ADC and FEC decoder,” IEEE Journal of Solid State Circuits, Vol. 33, No. 12, pp. 2205-2218, Dec. 1998.
- D. A. Byan, “QAM for terrestrial and cable transmission,” IEEE Transactions on Consumer Electronics, Vol. 41, No. 3, pp.383-391, Aug. 1995.
- B. D. O. Anderson and J. B. Moore, “Optimal Filtering”, Englewood Cliffs, New Jersey: Prentice-Hall, 1979.
- J. G. Proakis, “Digital Communications", 3rd edition, McGraw-Hill, 1995.
- S. Haykin, “Adaptive Filter Theory", Prentice-Hall, 3rd Ed., 1996.
- D. Stranneby& W. Walker, “Digital Signal Processing and Applications", NewenesAn Imprint of Elsevier, 2nd Edition, 2009.
- S. M. Kay, “Fundamentals of Statistical Signal Processing: Estimation Theory", Prentice-Hall, 1998.
- Grewal M. S., and Andrews A. P., “Kalman filtering, theory and practice", Prentice- Hall, 1993.
- Thomas Drumright, “Adaptive Filtering", Spring 1998.
- S. M. Kay, “Fundamentals of Statistical Signal Processing: Estimation Theory", Prentice-Hall, 1998.
|