Keywords
|
| Credit Risk Analysis; IBk Classifier; K Star Classifier |
INTRODUCTION
|
| Important activity of banking industry is to lend money to those who are in need of money. In order to pay back the principal borrowed from depositors, this industry collect interests on the payments made by the borrower. The borrowers, who fail to make their payments, have defaulted on their guarantee of settlement. To minimize the defaulter rate banking industry need to evaluate the credit details of borrowers. This needs improved research in credit risk assessment. This paper evaluates the Adeptness of Instance Based Classifiers and K Star Classifier for Credit Risk Assessment of banking customers and compared their results. These classifiers fall in the family of Memory based learning. Memory-based learning compares new problem instances with training instances, which are already available in memory. It got its name because it constructs hypotheses directly from the training instances themselves. It has different advantages like, very fast training, learning complex target functions easily, No information loss, and the ability to adapt its model to previously unseen data. Motivated by the need of such requirement, in this work, adeptness evaluation of Instance based classification and K Star Classifier for their suitability on credit data analysis is examined and compared. |
LITERATURE REVIEW
|
| Many researchers have made the analysis of credit risk using various computing techniques at different stages. A neural network based system for automatic support to credit analysis in a real world problem is presented in [1] & [2]. Hybrid method for evaluating credit risk using Kolmogorove-Smirnov test, DEMATEL method and a Fuzzy Expert system is explained in [3]. The credit risk for a Tunisian bank through modeling the default risk of its commercial loans is analyzed in [4]. An integrated back propagation neural network with traditional discriminant analysis approach is used to explore the performance of credit scoring in [5]. An application of artificial neural network to credit risk assessment using two different architectures are discussed in [6]. A comparative study of corporate credit rating analysis using support vector machines (SVM) and back propagation neural network (BPNN) is analyzed in [7]. Modeling framework for credit assessment models is constructed by using different modeling procedures and performance is analyzed in [8]. A triple-phase neural network ensemble technique with an uncorrelation maximization algorithm is used in a credit risk evaluation system to discriminate good creditors from bad ones is explained in [9].Artificial neural networks using Feedforward back propagation neural network and business rules to correctly determine credit defaulter is proposed in [10]. Credit risk analysis using different Data Mining models like C4.5, NN, BP, RIPPER, LR and SMO are compared in [11]. Credit risk assessment using six stage neural network ensemble learning approach is discussed in [12]. This research work compares the adeptness of Instance based classifier and K Star Classifier for the effective assessment of credit risk |
DATA USED FOR ANALYSIS
|
| The German credit data is taken for credit data analysis [13]. It consists of 20 attributes and 1000 instances. It has two classes, namely, good and bad. The class is obtained based on the values of all the 20 attributes. Table 1 lists the attributes of Credit-g dataset. |
METHODOLOGY USED
|
| The Classifiers used for its adeptness to do credit risk evaluation are listed below. |
| A. IBk Classifier |
| IBK is an implementation of the k-nearest-neighbor classifier. Each case is considered as a point in multi-dimensional space and classification is done based on the nearest neighbors. The value of ‘k’ for nearest neighbor can vary. This determines how many neighbors can be considered to decide how to classify an unknown instance. For example, for the ‘German credit’ data, IBK would consider the 20 dimensional spaces for the 20 input variables. A new instance would be classified as belonging to the class of its closest neighbor using Euclidean distance measurement. If the value of ‘k’ is 6, then 6 closest neighbors are considered. The class of the new instance is considered to be the class of the majority of the instances. If 6 is used as the value of k and 4 of the closest neighbors are of type ‘Good’, then the class of the test instance would be assigned as ‘Good’. The time taken to classify a test instance with nearest-neighbor classifier increases linearly with the number of training instances kept in the classifier. Its performance degrades rapidly with increasing noise levels. It also performs poor, when different attributes affect the outcome to different extents. One parameter that can affect the performance of the IBK algorithm is the number of nearest neighbors to be used. By default it uses just one nearest neighbor. |
| B. K Star Classifier |
| K-Star is a memory-based classifier that is the class of a test instance is based upon the class of those training instances similar to it, as determined by some similarity function. The use of entropy as a distance measure has several benefits. Amongst other things it provides a consistent approach to handling of symbolic attributes, real valued attributes and missing values. K* is an instance-based learner which uses such a measure [14]. |
| 1) Specification of K* |
| Let I be a (possibly infinite) set of instances and T a finite set of transformations on I. Each t ?? T maps instances to instances: t: I → I. T contains a distinguished member ?? (the stop symbol) which for completeness maps instances to themselves (?? (a) = a). Let P be the set of all prefix codes from T* which are terminated by σ. Members of T* (and so of P) uniquely define a transformation on I: t (a) = tn (tn-1 (... t1 (a) ...)) where t = t1...tn |
| A probability function p is defined on T*. It satisfies the following properties: |
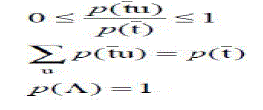 (1) (1) |
| As a consequence it satisfies the following: |
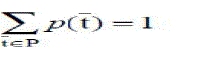 (2) (2) |
| The probability function P* is defined as the probability of all paths from instance ‘a’ to instance ‘b’: |
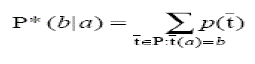 (3) (3) |
| It is easily proven that P* satisfies the following properties: |
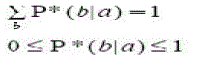 (4) (4) |
| The K* function is then defined as: |
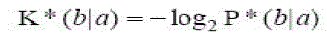 (5) (5) |
| K* is not strictly a distance function. For example, K*(a|a) is in general non-zero and the function (as emphasized by the | notation) is not symmetric. Although possibly counter-intuitive the lack of these properties does not interfere with the development of the K* algorithm below. The following properties are provable: |
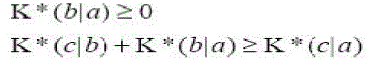 (6) (6) |
| The comparison of the results is made on the basis of the following criteria. |
| C. Accuracy Classification |
| All classification result could have an error rate and it may fail to classify correctly. So accuracy can be calculated as follows. |
| Accuracy = (Instances Correctly Classified / Total Number of Instances)*100 % (7) |
| D. Mean Absolute Error (MAE) |
| MAE is the average of difference between predicted and actual value in all test cases. The formula for calculating MAE is given in equation shown below: |
| MAE = (|a1 – c1| + |a2 – c2| + … +|an – cn|) / n (8) |
| Here ‘a’ is the actual output and ‘c’ is the expected output. |
| E. Root Mean Square Error (RMSE) |
| RMSE is used to measure differences between values predicted by a model and the values actually observed. It is calculated by taking the square root of the mean square error as shown in equation given below: |
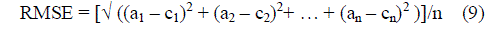 |
| Here ‘a’ is the actual output and c is the expected output. The mean-squared error is the commonly used measure for numeric prediction. |
| F. Confusion Matrix |
| A confusion matrix contains information about actual and predicted classifications done by a classification system. |
| The classification accuracy, mean absolute error, root mean squared error and confusion matrices were calculated using the machine learning tool. |
RESULTS AND DISCUSSION
|
| This work is carried out using Open Access Machine learning tool to evaluate the adeptness of instance based classifier and K-Star classifier for credit risk assessment. |
| G. Performance of IBk Classifier |
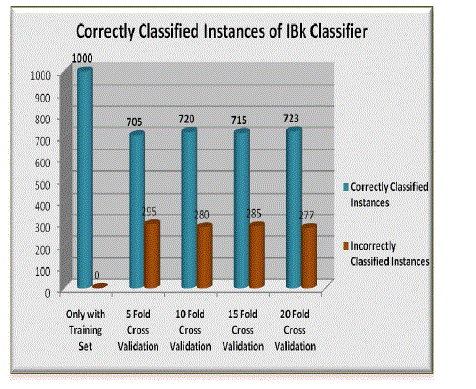
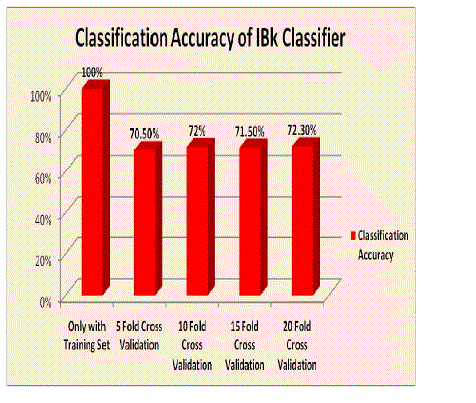
| The performance of the IBk classifier for credit risk analysis is shown below. Table 2 summaries the overall performance of IBk classifier in terms of Correctly Classified Instances, Classification Accuracy, Kappa statistics, RMSE and MAE values, etc. Table 3 to Table 7 shows the Confusion matrix of IBk classifier for the training data set and other Cross Validation (CV) techniques used. Correctly Classified instances of IBk classifier is shown in Fig 1 and the Classification Accuracy obtained by IBk classifier is shown in Fig 2. |
| H. Performance of K Star Classifier |
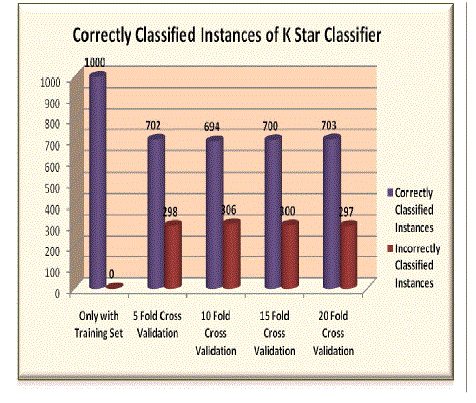
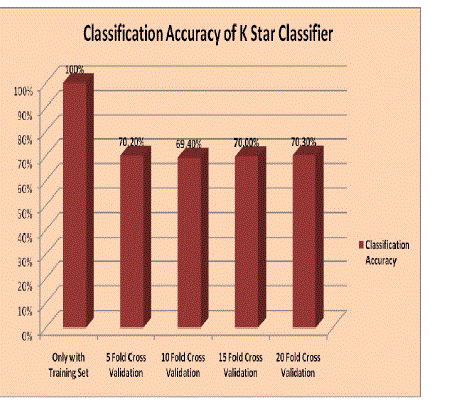
| The performance of the K Star classifier for credit risk analysis is shown below. Table 8 to Table 12 shows the Confusion matrix of K Star classifier for the training data set and other Cross Validation (CV) techniques used. Table 13 summaries the overall performance of K Star classifier in terms of Correctly Classified Instances, Classification Accuracy, Kappa statistics, RMSE and MAE values, etc. Correctly Classified instances of K Star classifier is shown in Fig 3 and the Classification Accuracy obtained by K Star classifier is shown in Fig 4. |
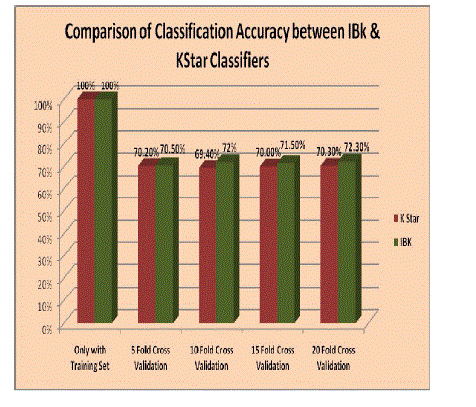
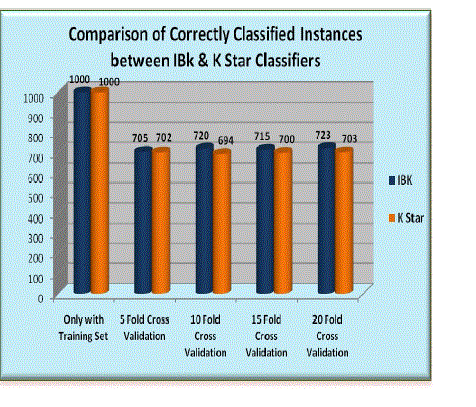
| The comparison between IBk classifier and K Star classifier are shown in Fig 5 and Fig 6 in terms of classification accuracy and Correctly Classified Instances. The overall ranking is done based on the classification accuracy, MAE and RMSE values and other statistics found using Training Set results and Cross Validation Techniques. Based on that, it is concluded that IBk classifier performs better than K Star. |
CONCLUSION
|
| This research work investigated the adeptness of Instance Based classifier and K Star Classifier for credit risk assessment. Experimentation is done using the open source machine learning tool. Adeptness evaluation of both classifiers has been done and a practical guideline for selecting the renowned and more suited algorithm for credit risk assessment is presented. After experimentation it is concluded that IBk Classifier performs better than K star Classifier in Credit Risk Assessment. |
ACKNOWLEDGMENT
|
| The author acknowledges the Management of IBS, Hyderabad for providing motivation and support. |
Tables at a glance
|
 |
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
Table 5 |
 |
 |
 |
 |
| Table 6 |
Table 7 |
Table 8 |
Table 9 |
 |
 |
 |
 |
| Table 10 |
Table 11 |
Table 12 |
Table 13 |
|
| |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
 |
 |
 |
| Figure 4 |
Figure 5 |
Figure 6 |
|
| |
References
|
- Germano C. Vasconcelos, Paulo J. L. Adeodato and Domingos S. M. P. Monteiro, “A Neural Network Based Solution for the Credit Risk Assessment Problem”, Proceedings of the IV Brazilian Conference on Neural Networks - IV Congresso Brasileiro de Redes Neurais pp. 269- 274, July 20-22, 1999 - ITA, São José dos Campos - SP – Brazil.
- Vincenzo Pacelli and Michele Azzollini, “An Artificial Neural Network Approach for Credit Risk Management”, Journal of Intelligent Learning Systems and Applications, 2011, 3, 103-112.
- Sanaz Pourdarab, Ahmad Nadali and Hamid Eslami Nosratabadi, “A Hybrid Method for Credit Risk Assessment of Bank Customers” , International Journal of Trade, Economics and Finance, Vol. 2, No. 2, April 2011.
- Hamadi Matoussi and Aida Krichene, “Credit risk assessment using Multilayer Neural Network Models - Case of a Tunisian bank” 2007.
- Tian-Shyug Lee, Chih-Chou Chiu, Chi-Jie Lu and I-Fei Chen, “Credit scoring using the hybrid neural discriminant technique”, Expert Systems with Applications (Elsevier) 23 (2002), pp. 245–254.
- Eliana Angelini, Giacomo di Tollo, and Andrea Roli “A Neural Network Approach for Credit Risk Evaluation”, Kluwer Academic Publishers, 2006, pp. 1 – 22.
- Zan Huang, Hsinchun Chena, Chia-Jung Hsu, Wun-Hwa Chen and Soushan Wu, “Credit rating analysis with support vector machines and neural networks: a market comparative study”, Decision Support Systems (Elsevier) 37 (2004) pp. 543– 558.
- Arnar Ingi Einarsson, “Credit Risk Modeling”, Ph.D Thesis, Technical University of Denmark, 2008.
- Kin Keung Lai, Lean Yu, Shouyang Wang, and Ligang Zhou, “Credit Risk Analysis Using a Reliability-Based Neural Network Ensemble Model”, S. Kollias et al. (Eds.): ICANN 2006, Part II, LNCS 4132, pp. 682 – 690, 2006.© Springer-Verlag Berlin Heidelberg.
- A.R.Ghatge, P.P.Halkarnikar, “ Ensemble Neural Network Strategy for Predicting Credit Default Evaluation” International Journal of Engineering and Innovative Technology (IJEIT) Volume 2, Issue 7, January 2013 pp. 223 – 225.
- S. Kotsiantis, “Credit risk analysis using a hybrid data mining model”, Int. J. Intelligent Systems Technologies and Applications, Vol. 2, No. 4, 2007, pp. 345 – 356.
- Lean Yu, Shouyang Wang, Kin Keung Lai, “Credit risk assessment with a multistage neural network ensemble learning approach”, Expert Systems with Applications (Elsevier) 34 (2008) 1434–1444.
- UCI Machine Learning Data Repository – http://archive.ics.uci.edu/ml/datasets.
- John G. Cleary, “K*: An Instance-based Learner Using an Entropic Distance Measure”.
|