Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

AGC AND AVR OF MULTI AREA POWER SYSTEMS WITH AND WITHOUT GRC NONLINEARITY

M. Nagendra1, Dr. M.S. Krishnarayalu2
  1. PG Student [PSE], Department of EEE, V.R.Siddhartha Engineering College, Vijayawada-520007, AP, India
  2. Professor, Department of EEE, V.R.Siddhartha Engineering College, Vijayawada-520007, A.P, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

A three area power system with Generation Rate Constraints (GRC) nonlinearity and a four area power system without GRC nonlinearity are considered. Load frequency and voltage control problems are studied with Automatic Generation Control (AGC) and Automatic Voltage Regulator (AVR) respectively using PID and fuzzy logic controllers for these Multi Area Power Systems (MAPS). The study shows that PID controller is more effective than fuzzy logic controller. For MAPS with GRC nonlinearity the system settles quickly with less peak overshoot when PID controller is used. For MAPS without GRC nonlinearity the system settles quickly when PID controller is used, even though the peak overshoot (undershoot) is more.

Keywords
Automatic Generation Control (AGC), Automatic Voltage Regulator (AVR), Multi Area Power Systems (MAPS), Proportional-Integral-Derivative (PID) Controller, Fuzzy Logic Controller (FLC), Generation Rate Constraints (GRC).

INTRODUCTION
Electric power system disturbances caused by load fluctuations result in changes to the desired frequency value. In MAPS when a load perturbation takes place in one area, it will affect the frequency of other areas also. To improve the stability of the power networks, it is necessary to design automatic generation control systems that control the power generation and active power [1-5]. The importance of AGC and AVR is well known in MAPS. AGC problem is solved by applying Area Control Error (ACE) as input to a PID controller [6]. Similarly AVR is achieved using PID controller.
PID controller is a very popular industrial controller. There are many methods available for tuning of PID controllers [7]. If properly tuned it gives superior performance. These days simulation software tools are widely popular. MATLAB Simulink is one of them. A method is proposed to tune PID controller using Simulink [6]. The same method is used here to tune PID controllers. Another important controller is Fuzzy Logic Controller (FLC). Fuzzy control methods are applied to AGC problem [8-12].
In this paper firstly we consider a three area MAPS with GRC nonlinearity. Then we consider a four area MAPS without GRC nonlinearity. We study performances of these systems using PID and fuzzy logic controllers.

SYSTEM
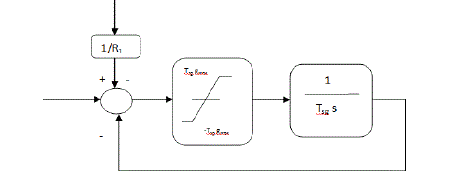
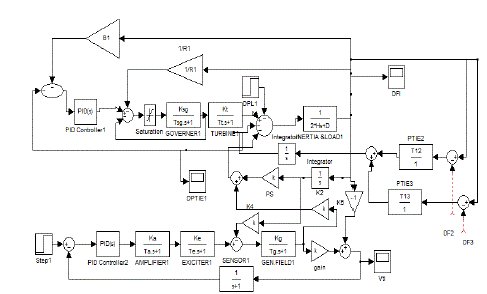
Simplified representation of three area power system shown in Fig. 1 and modeling of different components of power system are taken from [1]. Figs. 2 and 3 show the governor model with GRC, AGC and AVR model of Area- 1 of a three-area power system with GRC respectively.

Generation Rate Constraints
Maximum and minimum rates of change of power generation are called generation rate constraints in a power system. In power plants, power generation can change only at specified maximum rate. If generation increased above the specified limit then system may experience large momentary disturbance. This results in unnecessary stress on controller. One way of considering GRC is to add limiters to the governors as shown in Fig 2. Maximum rate of valve opening and closing speed is restricted by these limiters. Most of the reheat units have generation rate around 3%/min and some have generation rate between 5 to 10%/min [4].

CONTROLLERS

PID Controller
In order to keep the power system in normal operating state, a number of controllers are used in practice. Because of the inherent nonlinearities in system components and synchronous machines, most of the automatic generation controllers are primarily composed of an integral controller. The integrator gain is set to a level that compromise between fast transient recovery and low overshoot in the dynamic response of the overall system. This type of controller is slow and does not allow the controller designer to take into account possible non-linearity in the generator unit. . Hence the PID controller will be used for the stabilization of the frequency in the AGC problems. Here tuning of PID controller is very important to get optimal performance. The basic structure of a PID controller is
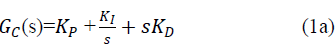image
where KP, KI and KD are proportional, integral and derivative gain constants. Proportional control results in decrease of rise time but also results in oscillatory performance. Derivative control reduces the oscillations by providing proper damping which results in improved transient performance and stability. Integral control reduces the steady state error to zero. Theoretically KP, KI and KD are to be selected from infinite combinations. Proper selection ensures the bull’s eye. In MATLAB, the transfer function of PID controller is
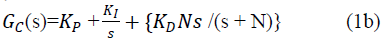where N sets the pole location of derivative filter. Default value of N is 100.
PID controller tuning can be achieved in three steps using MATLAB Simulink [6]. In Step 1 we select KP that results in a highly oscillatory stable response with KD = KI = 0. In Step 2 we fix the parameter KD, for KP selected in Step1, taking care of transient performance. In Step 3 we fix the parameter KI, for KP and KD selected in Steps 1 and 2, taking care of steady state performance. This completes the tuning of PID controller. Following this tuning method the resulting parameters of PID controller are given in Tables 3 and 4.

Fuzzy Logic Controller
Fuzzy Logic (FL) is a problem-solving control system methodology. It resembles human decision making with its ability to work from approximate data and find precise solution. Fuzzy controllers consist of three stages
1. Input stage
2. Processing stage and
3. Output stage.
The input stage maps inputs to the appropriate membership functions and truth values. The processing stage uses each appropriate rule and generates a result for each rule, then combines the results of all the rules. A fuzzy system knowledge base consists of fuzzy IF-THEN rules and membership functions characterizing the fuzzy sets. Output stage converts the combined result back into a specific control output value. In addition to input and output scaling factors are needed to modify the universe of discourse. Their role is to tune the fuzzy controller to obtain the desired dynamic properties of the process-controller closed loop.
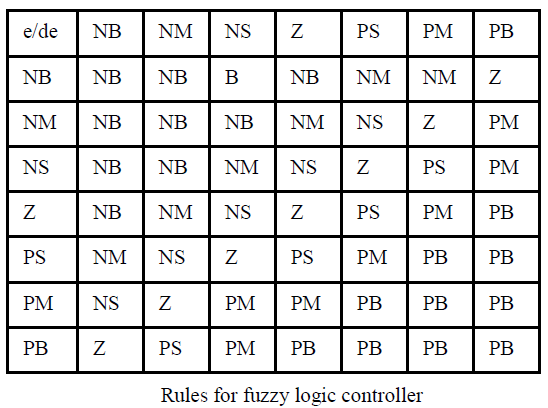
The inputs of the proposed Fuzzy controllers are area control error (ACE), and change rate in area control error (ΔACE) which is indeed error (e) and the derivation of the error (Δe) of the system, respectively. The type of the FLC obtained is called Mamdani type which has fuzzy rules of the form If ACE is Ai and ΔACE is Bi THEN u is Ci i=1 to n. Here Ai, Bi, Ci are the fuzzy sets. The triangle membership functions for each fuzzy linguistic values of the ACE and ΔACE are shown in Table in which NB, NM, NS, Z, PS, PM, and PB represent negative big, negative medium, negative small, zero, positive small, positive medium and positive big, respectively.
image

RESULTS AND DISCUSSIONS
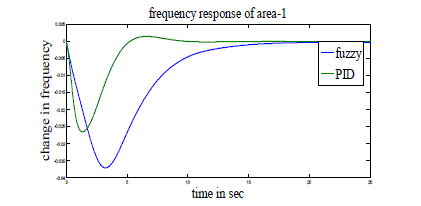
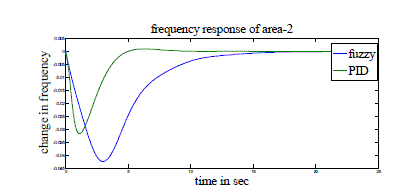
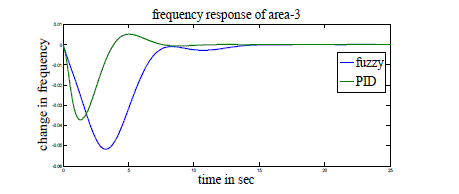
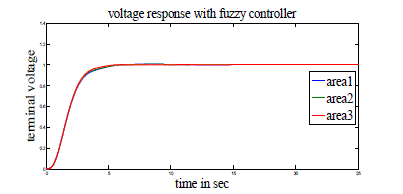
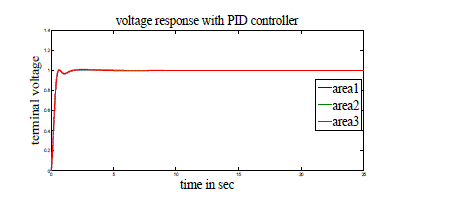
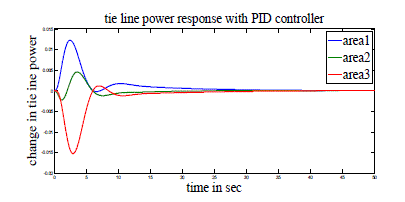
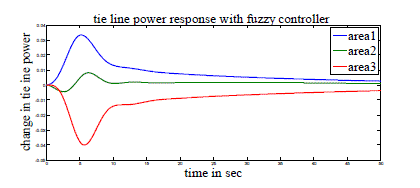
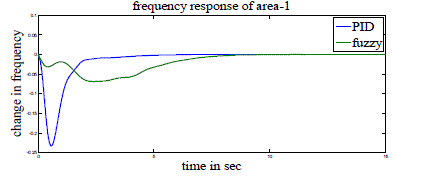
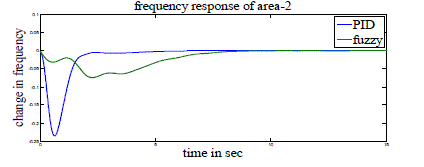
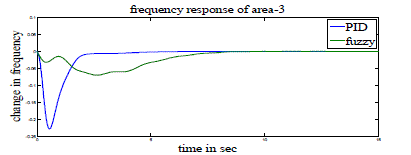
Case 1: Here three-area power system with GRC is considered. PID controllers of the form (1) are used in AGC and AVR modeling. These PID controllers are tuned as mentioned in [6] and shown in Tables 3 and 4. Simulation parameters used for AGC and AVR are shown in Tables 1 and 2 of Appendix. Figs 4-10 show the resulting responses with PID and Fuzzy controller considering GRC.
From all these figures we note that the results are better with PID controller compared to Fuzzy controller with less peak overshoot (undershoot) and settling time.
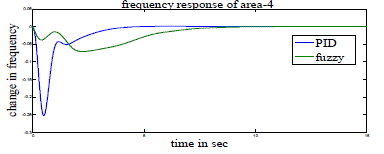
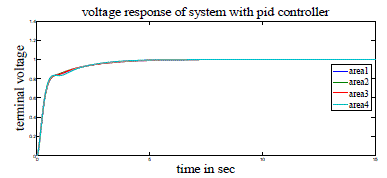
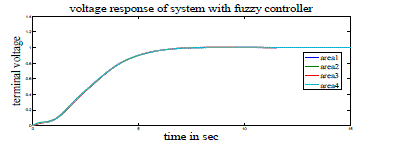
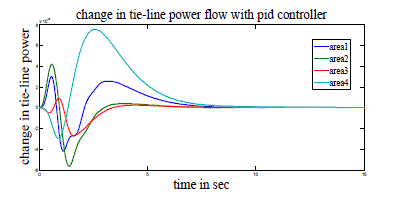
Case 2: Here a four area power system without GRC is considered and is modeled similar to three area system. This system is analyzed with PID controller tuned by method [6] and Fuzzy controller. Figs 11-18 show the frequency, voltage and tie line power response of this 4-area power system with PID and fuzzy controllers. Simulation parameters for AGC and AVR are shown in Tables 5 and 2 and PID parameters used in simulation are shown in tables 6 and 7 respectively in Appendix.
From these output responses we note that the settling time is less with PID controller whereas peak overshoot (undershoot) is less with fuzzy controller.

CONCLUSIONS
This paper presents the simulation of AGC and AVR of MAPS with and without GRC using Fuzzy and PID controllers. The results are compared. It is observed that PID controller [6] is better than fuzzy controller. Hence by proper tuning we can ensure better results from PID controller.

ACKNOWLEDGEMENTS
We greatly acknowledge Siddhartha Academy of General and Technical Education, Vijayawada for providing the facilities to carry out this research.
 

Tables at a glance
Table icon Table icon Table icon Table icon
Table 1 Table 2 Table 3 Table 4
Table icon Table icon Table icon
Table 5 Table 6 Table 7
 

Figures at a glance
Figure Figure Figure Figure Figure
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure Figure Figure Figure Figure
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10
Figure Figure Figure Figure Figure
Figure 11 Figure 12 Figure 13 Figure 14 Figure 15
Figure Figure Figure
Figure 16 Figure 17 Figure 18
 

References