Research and Reviews - International Journals

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Algorithms for Edge Detection and Enhancement for Real Time Images: A Comparative Study

Ashita Vermani1, Akshyata Ojha2
  1. Assistant Professor, Dept. of Electronics & Telecommunication., College of Engineering Roorkee, Roorkee, India
  2. Student, Dept. of Electronics & Telecommunication., College of Engineering Roorkee, Roorkee, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Thermal images are used for detection and identification of edges in any object due to varying atmospheric conditions. In this paper, five algorithms, viz, Robert, Sobal, Prewitt, laplacian and Canny edge detection algorithm are discussed and their performances are compared for optimal edge detection. Edge detection play a linchpin role in image analysis and able to solve complex problems, it is an important step to identify object segmentation and help in feature extraction. It basically works on grey level of pixels, it is used to track targets, compress data, recognition of object etc. as it significantly reduces amount of data and filters out useless information while preserving important structural properties. Performance of algorithms is decided in considering accuracy and speed.

Keywords
images, optimal edge detection, grey level of pixels, data compression

INTRODUCTION
To detect edges, we must have knowledge about infrared imaging/ thermal imaging. Thermal imaging is done to analyze objects in the dark with the help of black body radiation , all objects emit radiation above absolute zero temperature. With increase in temperature, emitted radiation will increase thus object appear brighter and clearer then cooler object. Thermo graphic cameras detect radiation in IR range and produce image called thermograms. Thermograms represent quantity of IR energy emitted transmitted and reflected by an object, but the controversy is that because of different IR energy sources, accurate temperature of the object can’t be measured.
Incident Energy= Emitted Energy + Transmitted Energy + Reflected Energy
Since Emissivity is the ability of material to emit thermal radiation with change in temperature. Its value is between zero to one and black body is the material which radiates IR radiation at its contact temperature, emissivity of true black body is one in practicality. The rate of emission of IR radiation produce fraction of true contact temperature and this fraction is called emissivity. Introduction of thermal imaging system is done for edge detection which has ability to see through smoke. It detects variation in temperature to differentiate between targets and their backgrounds. Because of their low cost, they are used in number of industrial and civil applications. Thermal imagers can scan @ 30 times per second and sense temperature ranging from -40 F to 36000 F.
In fig 1, Lens focuses the IR radiation emitted by the source object [1]. Phase array of IR detector scan the focus light and hereby detector elements create detailed temperature pattern i.e. thermogram. The thermogram then translated into electrical impulses. The impulses then sent to signal processing unit then that translate information into data for the display. The display appears in various colors depending on intensity of infrared emission and the combination of all impulses create image

RELATED WORK
In [7] A.P. Blicher, used methods of edge detection are discussed. Robert cross operator is first used in computer vision and image processing. It was proposed by Lawrence Robert in 1963, it calculates gradient of image followed by discrete differentiation .It is done by evaluating sum of the squares of the difference between diagonally adjacent pixels. Robert cross operator performs a simple quick two dimensional spatial gradient measurement is discussed in [9] in which pixel value at each point is output which represent the absolute magnitude of spatial gradient. W. Frei and C.C. Chen [10] used Sobel operator which is discrete differential operator which evaluate the approximation of gradient as intensity function. Sobel operator is based on convolving the image with small , separable, and integer valued filter in horizontal and vertical direction thus is relatively inexpensive . In[8], auhor used Prewitt operator in which image processing particularly for edge detection[2] used for high frequency variations. In the image it shows how abruptly or smoothly the image changes as the operator calculates the gradient of image intensity at each point by giving the direction of the largest possible increase front light to dark . W.M. Krueger and K. Phillips[4] used Canny edge detector also known as optimal detector[3] it follow the list of criteria to improve the current method of edge detection .The criteria includes low error rate ,no response to non edges , well localization of edge points ,minimal response to noise . X. Jing, Y. Nong, and Y. Shang[11] used Laplacian which is a two dimensional isotropic measure of second spatial derivative of the image.It highlights region of rapid intensity change, it uses two Gaussian and laplacian filter.

VARIOUS TECHNIQUES FOR EDGE DETECTION
Edge detection is a basic tool used in image processing. It is a process of identifying and locating sharp discontinuities of an image. Discontinuities are areas of abrupt pixel change by which boundaries of the object are characterized. It is used for feature detection and extraction, which aims to identify points in a digital image where brightness of image changes sharply and find discontinuities. Thus, applying an edge detection algorithm to an image may significantly reduce the amount of data to be processed and may therefore filter out information that may be regarded as less relevant, while preserving the important structural properties of an image. If the edge detection step is successful, the subsequent task of interpreting the information contents in the original image may therefore be substantially simplified. Traditional approach of edge detection involve convolution of image with 2D filter which is sensitive to large gradient. They give values of zero in uniform region. Edge detection operators have features like Edge Orientation, Noise Environment, Edge Structure.
There are two techniques:
Gradient Based: It detect edges by looking for maximum and minimum of first derivative. It includes sobel operator, prewitt operator, Roberts operator.
Laplacian Based: It searches zero crossings in the second derivative of image to find edges. It includes laplacian of Gaussian, Canny edge detection.
As we know edges have higher pixel intensity values than surroundings, so once threshold is set we compare the gradient value and detect an edge when threshold is exceeded. When first derivative is maximum, second derivative is zero.

METHODOLOGY
For evaluating the output and generating MATLAB code following steps are taken-
1. Accept a sample image in two dimensional domain
2. Apply mask Gx , Gy to the input image
3. Apply edge detection algorithms
4. Obtain mask manipulation of Gx and Gy separately on the input image
5. Combine result to obtain absolute magnitude of the gradient
6. Trace the absolute magnitude

SIMULATION RESULTS

A. Gradient based techniques:
a) Roberts Cross-Gradient Operator: It is used in image processing and computer vision for edge detection. It approximates the gradient of an image by discrete differentiation. Discrete differentiation is done by computing sum of the squares of differences between diagonally adjacent pixels. It quickly compute 2D spatial gradient of input image at that point.
Two kernels used as operator here. One kernel is 900 rotated form of other.
image
These kernels respond maximum to edge at 450 to pixel grid.
Gradient magnitude |G|=(Gx2+Gy2)1/2
Approximate magnitude |G|=|Gx|+|Gy|
Angle of orientation which will give rise to spatial gradient is α=arctan(Gy/Gx)-3π/4
As shown in fig 2 firstly we convert the image in 2-D then with the help of two kernals image is traced in xaxis and y-axis respectively .with the help of both x axis and y axis gradient magnitude and orientation is computed and final detected image is obtained

b) Sobels Operator:
It is discrete differentiation operator, calculates approximation of gradient of image intensity function. This operator works on convolution of image with small separable and integer valued filter in both directions. For high frequency, it produces crude gradient. The two kernels used here are Gx and Gy. For horizontal and vertical derivative approximation.
image
* 2D Convolution operation
Soble kernels= Averaging x differentiation kernel
They compute the gradient with smoothing, x coordinate increase in right direction and y coordinate in down direction. At each point gradient is approximated through
|G|=(Gx2+Gy2)1/2
And the gradient directions α=arctan(Gy/Gx)
α=0 for vertical edge
Intensity function at discrete point is known thus to define derivative of this function, we need to sample image point.
Only eight image points are needed to calculate gradient vector and two discrete filters are separable. As shown in fig3 x and y axis detection is followed by a figure in which edge is traced with the help of magnitude and orientation. When we calculate x axis gradient the Gx kernel is convolved with the image. Similarly for y axis detection we convolved y axis kernel with image.

c) Prewitt Operator:
The operator estimates gradient of image intensity giving largest possible increase from light to dark. Only the difference is of kernels. They are decomposed into averaging and differential kernel.
As shown in fig 4 for x axis detection we convolve Gx kernel with input image. The kernals taken are small and thus prevent blurring and other problems. Similarly after calculating y axis gradient by rotating Gx kernel by 900 we evaluate magnitude and orientation -
image

B. Gaussian Based Techniques:

 
Laplacian of Gaussain: (LOG Operator) It highlights regions of rapid intensity change. Laplacian is applied after application of smoothening and approximating Gaussain filter to image, thus sensitivity to noise is reduced. It takes single grey level image as input and produces another grey level image as output.
L(x,y)=Laplacian of image
I (x,y)= Pixel intensity values
L(x,y)=Δ2I/Δx2 + Δ2I/Δy2
It uses hybrid filter that is the combination of convolution of gaussian and laplacian filter
Three kernels used approximate second derivative which are usually small and very sensitive to noise
image
As shown in fig 5 applying log operator to the image and with the help of these three kernals the edge of the image can be detected .
Preprocessing step reduces high frequency noise component before differentiation here convolution is associative so we convolve Gaussian smoothing filter with laplacian filter. So there are two advantages, due to small kernels, fewer arithmetic operations are required and LOG operator kernel is pre-calculated so need to evaluate at runtime.
image

d) Canny Edge Detection:
It is most commonly used tool. This is usually used as standard edge detection method. Canny used many ways to approximate and optimize the edge detection problems. This detector has low error rate i.e. no response to non edges and the edge are well localized, i.e. difference between edge pixels in detector and actual edge should be minimum. Here the optimal detector provides good detection, good localization and minimal response. Four filters used to detect horizontal, vertical, diagonal in image.
|G|=(Gx2+Gy2)1/2
And α=arctan(Gy/Gx)
Convolution of raw image with Gaussian filter is used for noise reduction. It estimates image gradient by assuming local maxima in the gradient direction. It uses Hysteresis thresholding in which high thresholds are used to mark out edges roughly and eliminate noise pixels and low threshold are used for suppression.
More over there are two parameters used in this algorithm which are adjustable in nature thus provide flexibility and affect the computation time and effectiveness of algorithm. The parameters are:
1. The size of the Gaussian filter i.e. the smoothening filter used in first stage is small and hence cause less blurring and allow detection of small sharp lines. A larger filter causes more blurring so if we need to detect larger and smoother edges we can also use large blurring radii filter.
2. The use of two thresholds with hysteresis allow more flexibility then in a single threshold approach. However f the threshold is set too high it can miss the important information , on the other if it is set too low it will identify irrelevant information.So we have to fix accordingly.
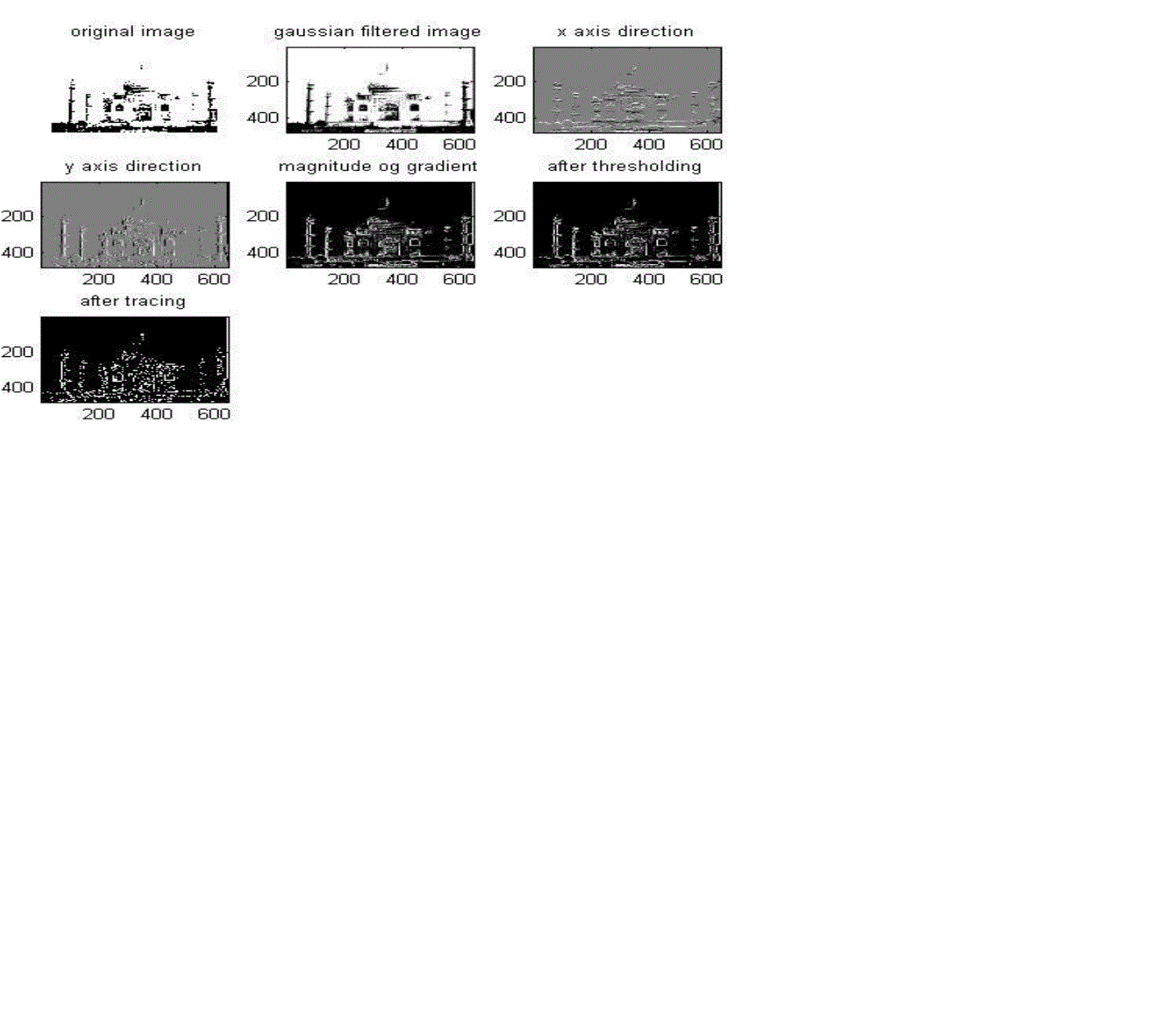
As shown in fig 6 the 2-D original image first passed through Gaussian filter to reduce noise then x axis gradient and y axis gradient is calculated same as in prewitt and sobal operator. The edge detected image is then subjected to thresholding and then traced.

CONCLUSION
The purpose of this paper is to compare various edge detection techniques using MATLAB software. We dealt with gradient based and laplacian based techniques. On the basis of above simulation results shown by fig 2, fig 3, fig 4, fig5 and fig 6. Edge tracing is done in x-axis, y-axis separately then combined result is shown by magnitude gradient, after thresholding, tracing is done. A satisfactory edge detection algorithm is the the one which provides error less solution and is adaptable to different noise levels. Canny algorithm is adaptable to various environment, its parameters allow it to recognize edges of unique characteristic. As the derivation of optimal filter results in finite impulse response (FIR),which makes computation slow in spatial domain thus Rachid Deriche’s infinite impulse response (IIR) is used as canny filter. It has features like recursion, short computation, fixed amount of time for desired smoothening .However it is bias towards horizontal and vertical edges thus it does not give good approximation of rational symmetry .Gradient based algorithms such as Prewitt filter has major drawback that they are sensitive to noise also size of kernel filter and coefficients is fixed so cannot adapt image. Canny’s edge detection is more expensive on the basis of computation however it performs better than all.

Figures at a glance
Figure Figure Figure Figure Figure
Figure 2 Figure 3 Figure 4 Figure 5 Figure 6

References