Keywords
|
| Voltage stability analysis, voltage collapse, voltage stability index, node sensitivity |
NOMENCLATURE
|
| Z Line impedance. |
| X Line reactance |
| QJ Reactive power at the receiving end |
| Vi Sending end voltage |
| Θ Line impedance angle |
| Δ Angle difference between the supply voltage and the receiving voltage |
| Pi Sending end real power |
| Pj Real power at the receiving end |
INTRODUCTION
|
| Voltage control problem are very much familiar to the electric utility industry are now receiving special attention by every power system analyst and researchers. With growing size along with economic and environmental pressures, the possible threat of voltage instability is becoming increasingly pronounced in the power system networks.[7] The voltage stability problem is now a serious concern to the electric utility industry. Many large interconnected power systems are increasingly experiencing abnormally high or low voltages and voltage collapse. These voltage problems are associated with the increased loading of transmission lines, insufficient local reactive supply, and the shipping of power across long distances. The heart of the voltage stability problem is the voltage drop that occurs when the power system experiences a heavy load, and one serious type of voltage instability is voltage collapse. Voltage collapse is characterized by an initial slow progressive decline in the voltage magnitude of the power system buses and a final rapid decline in the voltage magnitude [5]. |
| Electric power utilities are being under pressures by governments’ agency, politics, residential and industrial customers to provide reliable and uninterrupted service from power plants to loads. Unfortunately, a few utilities are able to construct new power plants and advance their systems targeting high reliability standard while others are forced to operate near their functioning design limits due economic and environmental constraints or because of the shortage in power delivery investment [3]. |
| Continuous monitoring of the system status is required because the voltage instability affects the satisfactory operation of power system. Stability of the power systems can be identified through various stability factors. The slow variation in reactive power loading towards its maximum point causes the conventional load flow solution to attain its non convergence point.[1]. Many of the researchers in the recent-past focused on the effective online monitoring of status of the system and hence to solve the problem of voltage collapse. In this regard, voltage stability index of each transmission line becomes the useful measure of power system monitoring. The index could identify how far a system is from its point of collapse. Performance indices to predict closeness to voltage stability boundary have been a permanent concern of researchers and power system operators, as these indices can be used online or offline to help dispatchers determine how close the system is to a possible voltage instability state Several voltage stability indices used to measure proximity to voltage collapse in off-line as well as on-line applications are described with great detail. A fast method for identification of the weakest bus.Sensitivity relates to the test's ability to identify positive results. The sensitivity of a test is the proportion of people that are known to have the disease who test positive for it. This can also be written as: Sensitivity = Probability of a positive test, given that the patient is ill. In load flow, sensitivity terms are used to find which nodes to generate a minimum voltage as compared to other nodes. Sensitive node is the one which is mostly suffered by the changes in load demands. For transmission network security & failure point of view it is quite important to calculate the most sensitive node in the network [2]. |
| In this review paper we have introduce some effective methods for finding weakest or critical bus with minimum time period and least value of weakest bus. |
METHODS ARE USED TO FIND SENSITIVE NODE
|
| There are several method are given for finding voltage sensitivity in different bus network applied at different situations. Description of these methods are following: |
| i). Line Stability Index Formulation (LSIF). |
| ii). Fast voltage stability index (FVSI). |
| iii). Voltage Collapse Prediction Index (VCPI). |
| iv). Modal Analysis. |
| v). TRGGQ: |
| vi). Voltage Sensitivity Factor (VSF). |
| vii). L-Index: |
| viii) Reactive Power Margin |
| xi). Line Stability Factor. |
| x). New Voltage Stability Index (NVSI). |
1).Line Stability Index Formulation
|
| Based on the transmission concept in a single line M. Moghavvemi’s derived a line stability index to find the voltage of an interconnected system in a reduced single line network, in this formulation the discriminator of the voltage quadratic equation is set to be greater or equal than zero to maintain stability. A typical single transmission line where index is derived from is illustrated in Fig. 1: |
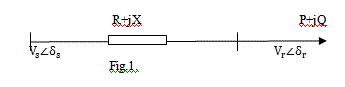 |
| Fig. 1. Single line diagram of a transmission line in the power system Where, Vs∠δs, Vr∠δr are the sending end and receiving end voltages. R+jX is the impedance of the transmission line P+jQ is the receiving end apparent power θ is |
| the line impedance angle δ is the angle difference between the supply voltage and the receiving end voltage. The line stability index is expressed by Lmn, proposed by Moghavvemi and Omar (1998) is formulated based on a power transmission concept in a single line. The line stability index Lmn is given by [1] |
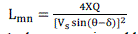 (1) (1) |
| When the stability index Lmn is less than 1, the system is stable and when this index exceeds the value 1, the entire system loses its stability and voltage collapse occurs. Hence the value of Lmn must be lower than 1 to maintain a stable system.[1] |
2).Fast voltage stability index(FVSI) :
|
| It is calculated using reactive power flow as, |
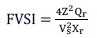 (2) (2) |
| The value of evaluated index close to 1 indicates that the particular line is near to instability point. The critical bus is determined by finding out the maximum permissible load on the bus. The most critical bus in the system is the bus which can bear smallest maximum load.[1] |
3). Voltage Collapse Prediction Index (VCPI):
|
 (3) (3) |
| VCPI is a voltage collapse indicator based on bus system and derived from power flow equation where the apparent power, Si, at any bus is expressed as: |
| Based on equation the voltage collapse prediction index is expressed as |
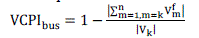 (4) (4) |
| VCPI varies from zero to one, indicating the voltage stability margin. Once the value of VCPI closes to unity or exceeds it, the system voltage collapses [2]. |
4).Modal Analysis:
|
| Modal analysis is used to computes eigenvalues and eigenvectors of a reduced Jacobian matrix of power flow to predict voltage instability in power systems. The eigenvalues of the reduced matrix determine the system mode while the eigenvectors gives an approximate measure to system instability. The equation of power flow is given by |
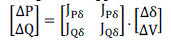 (5) (5) |
| whereΔP and ΔQ are the changes in the real and reactive powers while ΔV andΔδ are the deviations in bus Voltage magnitude and angle. If ΔP is assumed to be zero, the V-Q sensitivity is expressed as |
 (6) (6) |
| Where Jr = JQV - (JQδ. JPδ-1. JPV) By taking the right and left eigenvector matrix into account, the Jr matrix can be expressed as |
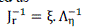 (7) (7) |
| where, ξ and η are the left and the right eigenvectors while Λ is the diagonal eigenvector matrix of Jrmatrix. Then, the V-Q sensitivity is expressed as |
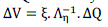 (8) (8) |
| Once the eigenvectors are normalized as it did in practice, ξi . ηi = 1 Where ∀i = 1.2,………n then the equation expressed as |
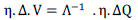 |
| Since η = η-1,the final ΔV and ΔQ relationship is expressed as ΔV = Ãâ°Ãâ¦-1. ΔQ |
| Where Ãâ°Ãâ¦-1 can be expressed in matrix form as |
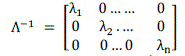 (10) (10) |
Hence, 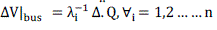 (11) (11) |
| For any i, if λ > 0, then the variation of Vi and Qi are in the same direction and the system is stable while the system is considered unstable when λ < 0 for any i. Once assumed ΔQ=0 in Eq. (7), the V-P sensitivity is established and expressed as |
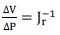 (12) (12) |
| Where Jr = JPV - (JPδ. JPδ-1. JQV) By taking the right and left eigenvector matrix into account, the Jr matrix can be expressed as. |
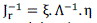 (13) (13) |
| By doing the same procedure, the V-P sensitivity is then expressed as |
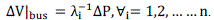 (14) (14) |
| For any i, if λ > 0, then the variation of Vi and Qiare in the same direction and the system is stable while the system is considered unstable when λ < 0 for any i.[2]. |
5).TRGGQ:
|
| TRGGQ is a voltage stability indicator used to screen the maximum available margin utilized in remedial scheme protection against cascaded voltage collapses. TRGGQ represents the gradient of the total reactive power generation with respect to the total active or reactive demand perturbations termed as TRGGQmpQ and TRGGQmpP where both indicescan be defined in any direction of load increase. The TRGGQmpQ is defined as the change rate of QGtotal with respect to a point of QD in the direction nmp and can be given by: |
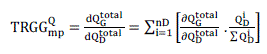 (15) (15) |
| The TRGGQpmp is defined as the change rate of QGtotal with respect to a point of PD in the direction nmp and can be given by: |
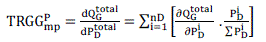 (16) (16) |
| and TRGGQpmp TRGGQmpP indices increase incrementally when the load increase gradually until reach to a point where both indices go to infinity or drop sharply to zero indicating voltage collapse.[2]. |
6).Voltage Sensitivity Factor
|
Voltage Sensitivity Factor Based on general concept, SF (sensitivity factor) index for a system represented by F (z,λ ) can be defined as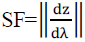 . when SF becomes large, the system turns insecure and ultimately collapses. Here the system voltages are checked with respect to the change in loading, which results in a Voltage sensitivity factor (VSF) calculated as . when SF becomes large, the system turns insecure and ultimately collapses. Here the system voltages are checked with respect to the change in loading, which results in a Voltage sensitivity factor (VSF) calculated as 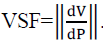 High sensitivity means even small changes in loading causes large changes in the voltage magnitude, which indicates the weakness of a bus.[3]. High sensitivity means even small changes in loading causes large changes in the voltage magnitude, which indicates the weakness of a bus.[3]. |
7). L-Index:
|
| L-index has been established as a fast voltage stability indicator for transmission system For an n-bus power system, buses can be separated into two groups: bringing all load buses to the head and denote them as αL and putting the generator buses to the tail and term them as i.e. αL = {1,2……nL-1, nL},αG={nL+1, nL+2……..nL-1,n},where nL is the number of load buses. With a multi-node system, |
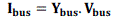 (17) (17) |
| By arranging the load buses αL and generator buses αG as mentioned earlier, equation (17) can be written as |
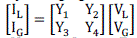 (18) (18) |
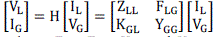 (19) (19) |
| Where ZLL, FLG, KFG,and YGG are sub-block of matrix H ; VG, IG, VL, IL are voltage and current vector of generator and load buses respectively. For any load bus j ∠ αL, stability index Lj can be expressed as |
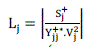 (20) (20) |
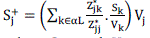 |
| Where Sk and Vk are complex power and complex voltage of node k respectively. The range of value is [0, 1]. Stability requires that Lj < 1 and must not be violated on a continuous basis. A global system indicator L describing the stability of the complete system is L= max ( Lj ) When L approaches 1.0; power system will approach voltage collapse. In practice L must be lower than a threshold value. The predetermined threshold value is specified at the planning stage depending on the system configuration and utility policy regarding quality of service.[3] |
8).Reactive Power Margin
|
| Reactive power margin for a load bus is measured as a distance between the lowest MVAr point of Q-V curve and Voltage axis as shown in Fig. 1 Thus reactive power margin indicates how further the loading on that particular bus can be increased before its loading limit is exhausted and voltage collapse takes place Reactive power margins are used in to evaluate voltage instability problems for coherent bus groups. These margins are based on the reactive reserves on generators, SVCs and synchronous condensers that exhaust reserves in the process of computing a Q-V curve at any bus in a coherent group or voltage control area. In this study, the reactive power margin index is used to measure the strength of the buses of a primary distribution network for different sets of load models.[3]. |
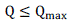 (22) (22) |
9). Line Stability Factor (LQP) :
|
| The LQP was used in the comparison since this factor is more sensitive to change in reactive power. The formulation begins with the power equation in a power system and finally LQP [15] is expressed as |
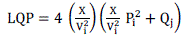 (23) (23) |
| All the above said indices have effectively shown the variation of reactive power load but not real power load. Most of these indices have been derived from the receiving end reactive power equation of transmission line. Instead of that, the index solved by considering the receiving end real power equation, it depends the resistance of the transmission line. However, the resistance values are negligible or even zero in standard and practical line data, and hence the index remains either infinite or zero.[4]. |
10).New Voltage Stability Index (NVSI)
|
| NVSI may be mathematically explained as follows: |
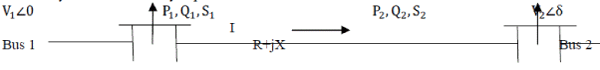 |
| Figure 2: Line Mode |
| From the Fig. 2, current flowing between bus 1 and 2, |
| Comparatively resistance of transmission line is negligible. The equation may be rewritten a and the receiving end power, S=V2I* Incorporating and solving this is an equation of order two of V2. The condition to have at least one solution is: Taking the suffix “i” as the sending bus & “j” as the receiving bus, NVSI can be defined by |
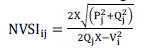 (24) (24) |
| The procedure to estimate the NVSI in all transmission lines in power system is shown in Fig. 2. The value of NVSI must be less than 1.00 in all transmission lines to maintain a stable system. |
| The merits of the index are that it relates both real and reactive power whereas other indices relate only the reactive power of the system. Moreover usage of fuzzy logic method produces more accurate and exact results. The number of mappings is reduced from 7 to 3 outperforming the existing methods. |
CONCLUSION
|
| Main aim of this paper was to introduce the voltage stability problem along with possible analytical solution.Line Stability Index Formulation [1] & Fast voltage stability index(FVSI).[1] method applied on IEEE 14 bus system and increased Load step by step and it is observed that bus 9 and 14 are most critical buses and when subjected to change in load may result in voltage collapse.The results of performed indices were compared to alternative methods to verify their accuracy for two loading scenarios. TRGGQq and VCPI are indices for the first scenario in which the IEEE 57- bus system was subjected to load increase. All indices started with system initial state and ended at the same voltage collapse point at loading rate k =0.39. VCPI has an advantage of providing voltage stability indications at each individual bus while the proposed sensitive indices along with TRGGq have a great sensitivity to system voltage collapse based on active and reactive powers which can be used in load-generation balance. |
| The weakest bus is defined as the bus which has very low reactive power maximum loadability and the most critical line means the line which is connected in the weakest bus, reaches the stability index closer to unity. Voltage Sensitivity Factor, L-Index, Reactive Power Margin [3] method applied on 16 bus Distribution system the highest value of VSF and L-index establish bus 7 as the weakest bus. For example, for constant power load models, lowest min Q arg 22.94MVAr has been found with bus 7, which establishes it as the weakest bus. The finding is in complete agreement with VSF and L-index which have highest values at, 0.53 and 0.22 respectively, to prove bus 7 as the weakest bus .We have reviewed new approaches of voltage stability analysis projecting successfully the point of voltage collapse. Though load model plays significant role in occurrence of voltage collapse and instability problems, .So the above said methods, which can be used irrespective of load types, is required to identify the weakest bus and take protective measures. |
| |
Tables at a glance
|
 |
| Table 1 |
|
| |
References
|
- P.R. Sharma, Rajesh Kr.Ahuja, Shakti Vashisth, Vaibhav Hudda Department of Electrical Engineering, YMCAUST, Faridabad1, 2, 3 Department of Electrical Engineering, AKGEC, Gaziabad4 “Computation of Sensitive Node for IEEE- 14 Bus system Subjected to Load Variation “INTERNATIONAL JOURNAL OF INNOVATIVE RESEARCH IN ELECTRICAL, ELECTRONICS, INSTRUMENTATION AND CONTROL ENGINEERING Vol. 2, Issue 6, June 2014 .
- F.A. Althowibi,M.W. Mustafa 2PhD Student, Dept. of EPE, UniversitiTeknologi Malaysia, Skudai, Johor, Malaysia 1Professor, Dept. of EPE, UniversitiTeknologiMalaysia,Skudai, Johor, Malaysia 2 “Voltage Collapse Sensitivity in Power Systems” International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering,Vol. 2, Issue 7, July 2013.
- Tareq Aziz, Student Member, IEEE, T. K. Saha , Senior Member, IEEE and N. Mithulananthan , Member, IEEE School of Informtaion Technology and Electrical Engineering The University of Queensland, St. Lucia Brisbane, Australia E-mail address: taziz@itee.uq.edu.au“Identification of the weakest bus in a distribution system with load uncertainties using reactive power margin”.
- R. Kanimozhi† and K. Selvi* Corresponding Author: Dept. of Electrical and Electronic Engineering, Anna University, BITCampus, Thiruchirapalli, Tamilnadu, India (kanimozhi_17@yahoo.com) * Dept. of Electrical and Electronic Engineering, Thiagarajar College of Engineering, Madurai, Tamilnadu, India (kseee@tce.edu) Received: October 18, 2012; Accepted: February 19, 2013“A Novel Line Stability Index for Voltage Stability Analysis andContingency Ranking in Power System Using Fuzzy Based Load Flow” J ElectrEngTechnol Vol. 8, No. 4: 694-703, 2013 http://dx.doi.org/10.5370/JEET.2013.8.4.694
- Byung Ha Lee and Kwang Y. Lee, Senior Member Transactions on Power Systems, Vol. 6, No. 3, August 1991 “A STUDY ON VOLTAGE COLLAPSE MECHANISM IN ELECTRIC POWER SYSTEMS” Department of Electrical and Computer Engineering The Pennsylvania State University University Park, PA 16802.
- ArunPachori, Asso. Prof. JEC, Jabalpur (MP), India ,2).HemantAmhia, (Asst. Prof.) JEC, Jabalpur (MP),India, VikendraMoranya, JEC, Jabalpur (MP),India International journals of emerging trend in Electronics and computer Science (IJETECS) Volume2,Issue9,sept2013. “Optimal Location of Static VAR Compensator in IEEE- 14 bus Power System at Varying Load Conditions”
- Power System Engineering, Second Edition by D.P.Kothari,I.J.Nagrath.
- PUSHPENDRA MISHRA, 2H. N. UDUPA, 3PIYUSH GHUNE1Research Scholar - MIT, Indore, 2Dean Academics - MIT, Indore, 3Assistant Professor – MIT, Indore E-Mail: mishrapushpendra08@gmail.com, hnudupa@gmail.com, piyushghune@yahoo.com“CALCULATION OF SENSITIVE NODE FOR IEEE – 14 BUS SYSTEM WHEN SUBJECTED TO VARIOUS CHANGES IN LOAD”Proceedings of IRAJ International Conference, 21st July 2013, Pune, India, ISBN: 978-93-82702-22-1
- Multiple Distributed Generator Placement in Primary Distribution Networks for Loss Reduction Duong Quoc Hung, Student Member, IEEE, and NadarajahMithulananthan, Senior Member, IEEE.
- Voltage Collapse Sensitivity in Power Systems F.A. Althowibi 1 ,M.W. Mustafa 2 PhD Student, Dept. of EPE, UniversitiTeknologi Malaysia, Skudai, Johor, Malaysia 1 Professor, Dept. of EPE, UniversitiTeknologiMalaysia,Skudai, Johor, Malaysia 2.
- The Judgment of Voltage Weak Point Method based on eigenvalue structure analysis Xiong Hu School of Electrical Engineering Wuhan University Wuhan, China xh5233063@163.comXiang Tieyuan School of Electrical Engineering Wuhan University Wuhan, China xty01@163.com 978-1-4244-6255-1/11/$26.00 ©2011 IEEE.
- RENWEABLE ENERGY RESOURCES AND DISTRIBUTED GENERATION IN INDIA Deepak Pandey1, Jitendra Singh Bhadoriya2, M.Tech(Research Scholar),Dept. of Electrical & Electronics Engineering ,NRI Institute of Information Science & Technology, Bhopal(M.P.),India 1 Asst. Professor, Dept. of Electrical & Electronics Engineering ,NRI Institute of Information Science & Technology, Bhopal(M.P.),India 2.
|