Keywords
|
| Sequential pattern mining, Progressive databases, Classification of algorithms. |
INTRODUCTION
|
| Data mining [Chen et al. 1996] is the process of extracting interesting (non-trivial, implicit, previously unknown and potentially useful) information or patterns from large information repositories such as: relational database, data warehouses, XML repository, etc. Also data mining is known as one of the core processes of Knowledge Discovery in Database (KDD).Usually there are three processes in KDD. One is called pre processing, which includes data cleaning, integration, selection and transformation. The main process of KDD is the data mining process, in this process different algorithms are applied to produce hidden knowledge. After that comes another process called post processing, which evaluates the mining result according to users? requirements and domain knowledge? Regarding the evaluation results, the knowledge can be presented if the result is satisfactory, otherwise we have to run some or all of those processes again until we get the satisfactory result. Various data mining techniques are applied to the data source; different knowledge comes out as the mining result. Those knowledge are evaluated by certain rules, such as the domain knowledge or concepts. After we get the knowledge, the final step is to visualize the results. They can be displayed as raw data, tables, decision trees, rules, charts, data cubs or 3D graphics. |
Types of Mining
|
| There are two classes of data mining descriptive and prescriptive. Descriptive mining is to summarize or characterize general properties of data in data repository, while prescriptive mining is to perform inference on current data, to make predictions based on the historical data. There are various types of data mining techniques such as association rules, classifications and clustering. Based on those techniques web mining and sequential pattern mining are also well researched. Association rule mining, one of the most important and well researched techniques of data mining, was first introduced in [Agrawal et al. 1993]. It aims to extract interesting correlations, frequent patterns, associations or casual structures among sets of items in the transaction databases or other data repositories. |
SEQUENTIAL PATTERN MINING
|
| Sequential pattern mining is an important data mining problem, which detects frequent sub sequences in a sequence database. The major techniques for sequential pattern mining are |
| 1. Apriori-based Approaches |
| – GSP |
| – SPADE |
| 2. Pattern-Growth-based Approaches |
| – FreeSpan |
| – PrefixSpan |
| Data are changing all the time; especially data on the web are highly dynamic. As time goes, new datasets are inserted; old datasets are deleted while some other datasets are updated. It is observable that time stamp is an important attribute of each dataset, also it is important in the process of data mining and it can give us more accurate and useful information. A database consists of sequences of values or events that change with time is called a time-series database [Han and Kamber 2000], a time-series database records the valid time of each dataset. Time-series database is widely used to store historical data in a diversity of areas such as, financial data, medical data, and scientifical data and so on. Different mining techniques have been designed for mining time-series data [Han and Kamber 2000], basically there are four kinds of patterns we can get from various types of time-series data: |
| A. Trend analysis: Trend analysis is to find the evolution patterns of attributes over time; they can be long-term trend movements, cyclic movements or variations, seasonal movements and irregular/random movements. |
| B. Similarity search: Similarity search tries to find sequences that differ only slightly. Similarity searching is a blurry matching process that can tolerate some differences within a certain threshold. Based on the length of sequences we are trying to match, sequence matching can be classified as: subsequence matching and whole sequence matching. |
| C. Sequential patterns: Sequential pattern mining is trying to find the relationships between occurrences of sequential events, to find if there exists any specific order of the occurrences. We can find the sequential patterns of specific individual items; also we can find the sequential patterns cross different items. Sequential pattern mining is widely used in analyzing of DNA sequence. |
| D. Periodical patterns: Periodical patterns are those recurring patterns in the time series database; periodicity can be daily, weekly, monthly, seasonal or yearly. Obviously, periodical patterns mining can be viewed as sequential pattern mining by taking the periodical sequences as a set of sequences. Sequential database is a special case of time series database, consequently most researches in sequential pattern mining focus on two main issues. The first issue is sequential pattern mining, aiming at finding the frequently occurred sequences to describe the data or predict future data. The second issue is periodical pattern mining, which can be viewed as sequential pattern mining. |
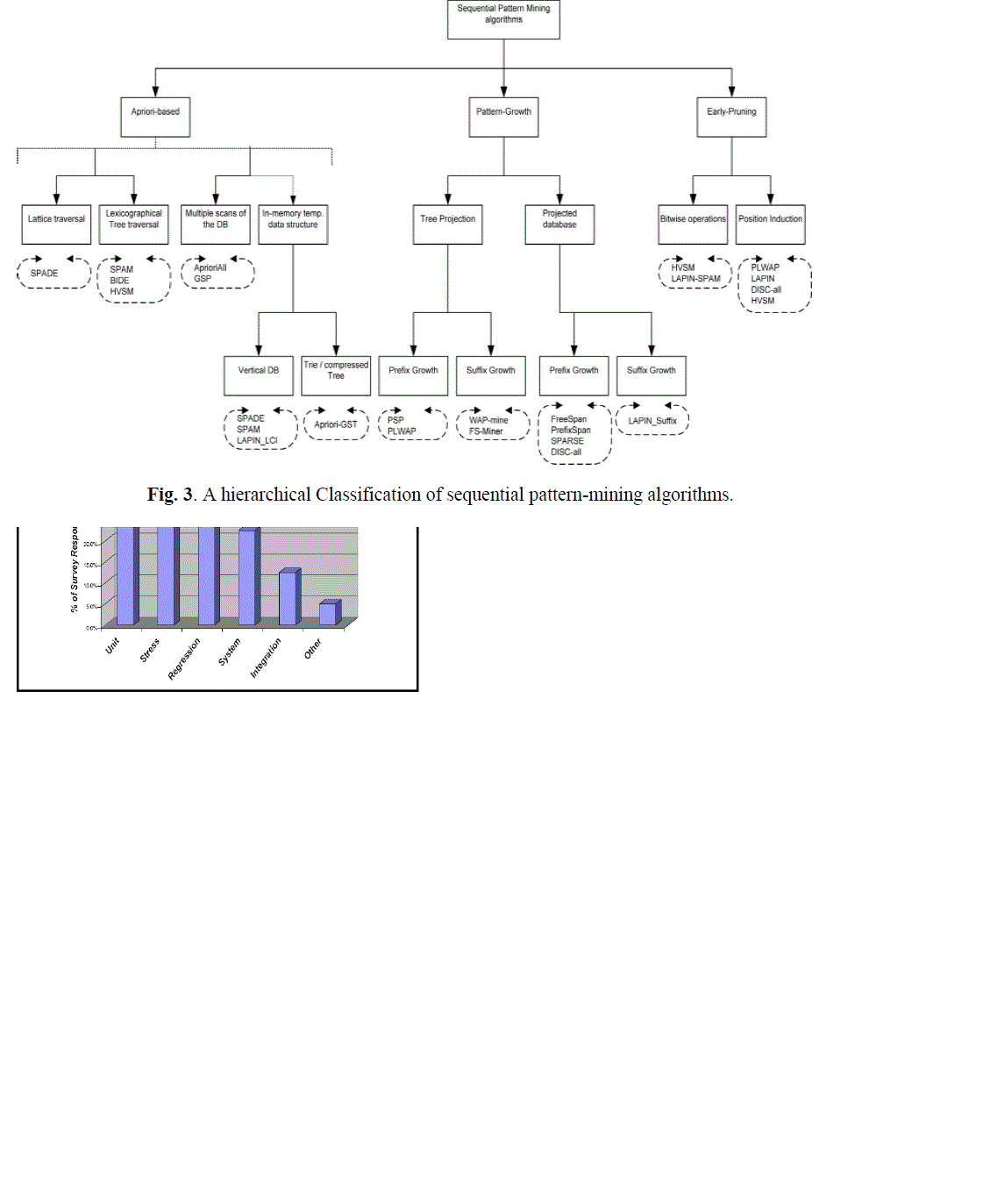
A CLASSIFICATION OF SEQUENTIAL PATTERN-MINING ALGORITHMS
|
| A Classification of existing sequential pattern-mining algorithms is provided in Figure 1 in this part, which lists the algorithms, showing a comparative analysis of their different important features. This proposed classification is composed of three main categories of sequential pattern-mining algorithms, namely, apriori-based, pattern-growth and Early Pruning algorithms. These features are a result of careful investigation of the surveyed algorithms and represent a superset of features usually discussed in the literature. |
| Frequent sequential pattern discovery can essentially be thought of as association rule discovery over a temporal database. While association rule discovery [Agrawal et al. 1993] covers only intratransaction patterns (itemsets), sequential pattern mining also discovers intratransaction patterns (sequences), where ordering of items and itemsets is very important, such that the presence of a set of items is followed by another item in a time-ordered set of sessions or transactions. The set of all frequent sequences is a superset of the set of frequent itemsets. Due to this similarity, the earlier sequential pattern-mining algorithms were derived from association rule mining techniques. The first of such sequential pattern-mining algorithms is the AprioriAll algorithm [Agrawal and Srikant 1995], derived from the Apriori algorithm [Agrawal et al. 1993; Agrawal and Srikant 1994]. An algorithm can fall into one or more (hybrid algorithms) of the categories in the proposed taxonomy. Algorithms mainly differ in two ways: |
| (1) The way in which candidate sequences are generated and stored. The main goal here is to minimize the number of candidate sequences generated so as to minimize I/O cost. |
| (2) The way in which support is counted and how candidate sequences are tested for frequency. The key strategy here is to eliminate any database or data structure that has to be maintained all the time for support of counting purposes only. The data structures used to store candidate sequences have also been a research topic and an important heuristic for memory utilization. |
A. Features for Apriori-Based Algorithms
|
| The Apriori [Agrawal and Srikant 1994] and AprioriAll [Agrawal and Srikant 1995] set the basis for a breed of algorithms that depend largely on the apriori property and use the Apriori-generate join procedure to generate candidate sequences. The Apriori property states that “All nonempty subsets of a frequent itemset must also be frequent”. It is also described as anti monotonic (or downward-closed), in that if a sequence cannot pass the minimum support test, all of its super sequences will also fail the test. |
| Given a database of web access sequences D over J items, and two sets X,Y ⊆ J , then X ⊆ Y ⇒ support(Y) ≤ support(X) . Hence, if a sequence is infrequent, all of its supersets must be infrequent; and vice versa, if a sequence is frequent, all its subsets must be frequent too. This anti monotonicity is used for pruning candidate sequences in the search space, and is exploited further for the benefit of most pattern growth algorithms. |
| Algorithms that depend mainly on the apriori property, without taking further actions to narrow the search space have the disadvantage of maintaining the support count for each subsequence being mined and testing this property during each iteration of the algorithm, which makes them computationally expensive. To overcome this problem, algorithms have to find a way to calculate support and prune candidate sequences without counting support and maintaining the count in each iteration. Most of the solutions provided so far for reducing the computational cost resulting from the apriori property use a bitmap vertical representation of the access sequence database [Zaki 1998; Ayers et al. 2002; Yang and Kitsuregawa 2005; Song et al. 2005] and employ bitwise operations to calculate support at each iteration. |
| All key features of apriori-based methods that pose challenging problems are as follow: |
| (1) Breadth-first search: Apriori-based algorithms are described as breath-first (level-wise) search algorithms because they construct all k-sequences together in each kth iteration of the algorithm as they traverse the search space. |
| (2) Generate-and-test: This feature is introduced by the Apriori algorithm [Agrawal et al. 1993] and is used by the very early algorithms in sequential pattern mining. In BIDE (an algorithm for mining frequent closed sequences [Wang and Han 2004]), it is referred to as “maintenance-and-test”. It entails using exhaustive join operators (e.g., Apriori-generate, GSP-join), in which the pattern is simply grown one item at a time and tested against the minimum support. Algorithms that depend on this feature only display an inefficient pruning method and generate an explosive number of candidate sequences, consuming a lot of memory in the early stages of mining. |
SEQUENTIAL PATTERN-MINING ALGORITHMS
|
| The surveyed algorithms are presented in this section. Section 4.1 reviews apriori-based algorithms; Section 4.2 summarizes pattern growth algorithms; and Section 4.3 discusses hybrid algorithms. |
4.1. Apriori-Based Techniques
|
| 4.1.1. AprioriAll [Agrawal and Srikant 1995] . AprioriAll scans the database several times to find frequent itemsets of size k at each kth-iteration (starting from k = 2). It also has the generate-and-test feature by performing the Apriorigenerate join procedure [Agrawal and Srikant 1994] to join Lk−1 with itself to generate Ck, the set of candidate sequences in the kth-iteration, it then prunes |
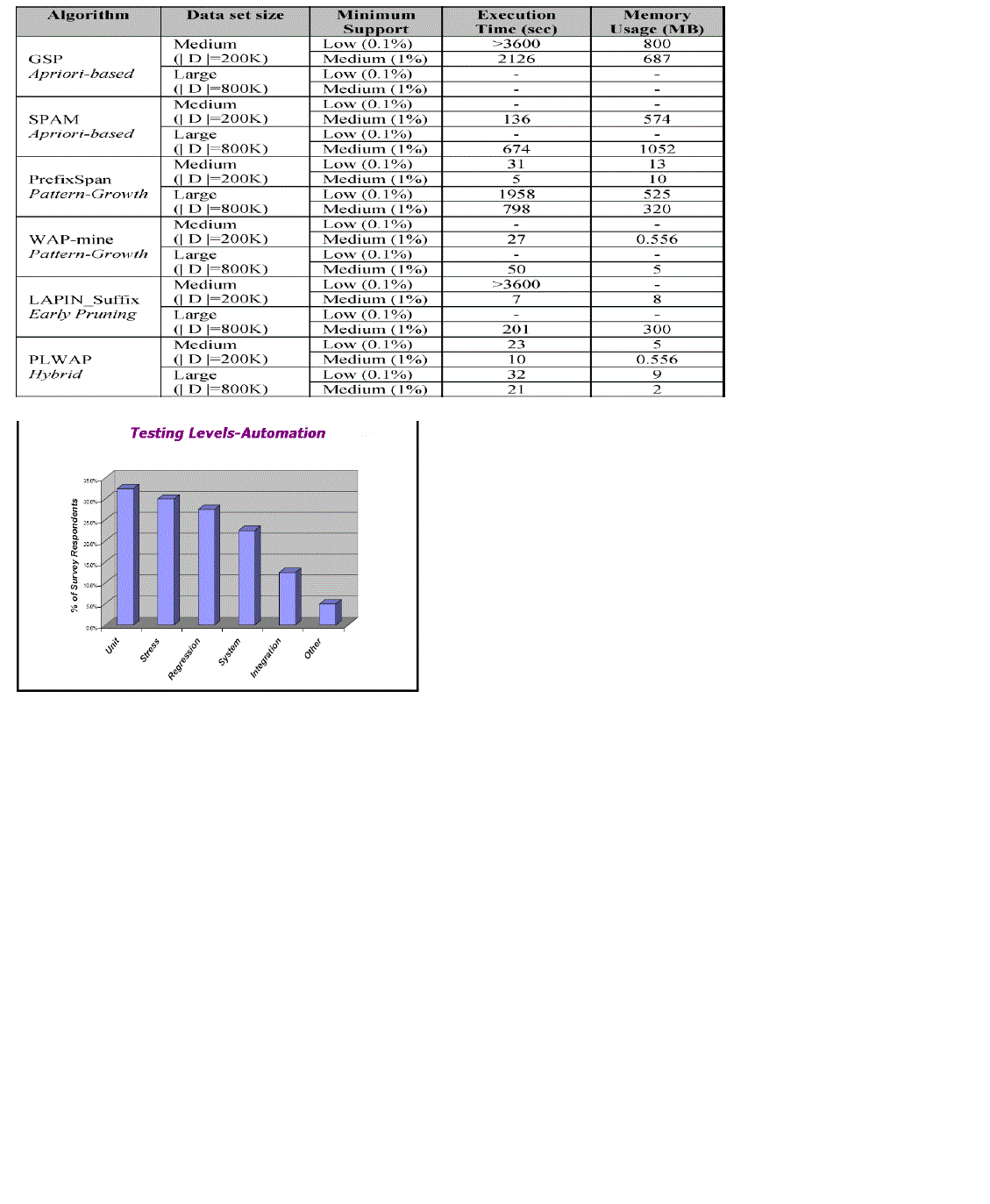
| The symbol “-” means an algorithm crashes with the parameters provided, and memory usage could not be measured.sequences in Ck which have subsequences not in Lk−1 (i.e., are not large), creates Lk by adding all sequences from Ck with support ≥ min sup until there are no more candidate sequences. The AprioriAll technique suffers from increased delays in mining as the number of sequences in the database gets larger. It also suffers from exponential growth of candidate sequences during execution. Several solutions were presented, including hashing to reduce the size of the candidate sequences [Park et al. 1995]; transaction reduction [Agrawal and Srikant 1994; Han and Fu 1995]; database partitioning [Savasere el al. 1995]; sampling [Toivonen 1996]; and dynamic itemset counting [Brin et al. 1997]. |
| 4.1.2. GSP [Srikant and Agrawal 1996] . The GSP algorithm, running on database D adopts a multiple-pass candidate generate-and-test method for finding sequential patterns. The GSP-join, like the apriori-generate join requires that two sequences in Lk join . |
| The prune phase deletes candidate sequences that have a contiguous (k − 1)-subsequence with support less than min sup. Each candidate sequence has one more item than a seed k-sequence, so all candidate sequences are the same number of items at each level. Support for these candidate sequences is again found during a pass over the data. The algorithm terminates when no new sequential pattern is found in a pass, or no candidate sequence can be generated. For increased efficiency, GSP employs a hash-tree to reduce the number of candidates in C that are checked for sequences. Note that, at each step, GSP only maintains in memory the already discovered patterns and the k-candidates, thus making it not a memory-only algorithm. GSP is reported to be 2 to 20 times faster than AprioriAll. |
| 4.1.3. PSP[Masseglia et al. 1999] . This is another apriori-based algorithm, also built around GSP, but the difference of using a prefix-tree. In PSP [Masseglia et al. 1999], user access sequences are sorted in the web log according to the IP address. The user is allowed to provide a time period _t by which access sequences that are temporally close to each other are grouped. A prefix-tree is then built to handle the mining procedure in a way similar to GSP. Following up on tree traversal, graph traversal mining was proposed by Nanopoulos and Manolopoulos [2000], which uses a simple unweighted graph to reflect the relationship between pages of websites. The algorithm is similar to apriori, without performing the Apriori-generate join. The database still has to be scanned several times, but it is more efficient than GSP. |
| 4.1.4. SPAM [Ayers et al. 2002] . SPAM integrates the ideas of GSP, SPADE, and FreeSpan. The entire algorithm with its data structures fits in main memory, and is claimed to be the first strategy for mining sequential patterns to traverse the lexicographical sequence tree in depth-first fashion. SPAM traverses the sequence tree in depth-first search manner and checks the support of each sequence-extended or itemset-extended child against min sup recursively. If the support of a certain child s is less than min sup, there is no need to repeat depth-first search on s by the Apriori property. Apriori-based pruning is also applied at each S-Step and I-Step of the algorithm, minimizing the number of children nodes and making sure that all nodes corresponding to frequent sequences are visited. |
4.2. Pattern-Growth Techniques
|
| Soon after the apriori-based methods of the mid-1990s, the pattern growth-method emerged in the early 2000s, as a solution to the problem of generate-and-test. The key idea is to avoid the candidate generation step altogether, and to focus the search on a restricted portion of the initial database. The search space partitioning feature plays an important role in pattern-growth. Almost every pattern-growth algorithm starts by building a representation of the database to be mined, then proposes a way to partition the search space, and generates as few candidate sequences as possible by growing on the already mined frequent sequences, and applying the apriori property as the search space is being traversed recursively looking for frequent sequences. PrefixSpan is based on recursively constructing the patterns by growing on the prefix, and simultaneously, restricting the search to projected databases. This way, the search space is reduced at each step, allowing for better performance in the presence of small support thresholds. PrefixSpan is still considered a benchmark and one of the fastest sequential mining algorithms alongside SPADE. Another algorithm, WAP-mine [Pei et al. 2000] is the first of the pattern-growth algorithms to use a physical tree structure as a representation of the sequence database along with support counts, and then to mine this tree for frequent sequences instead of scanning the complete sequence database in each step. |
| 4.2.1. FreeSpan [Han et al. 2000] . FreeSpan stands for Frequent Pattern-Projected Sequential Pattern Mining, and starts by creating a list of frequent 1-sequences from the sequence database called the frequent item list (f-list), it then constructs a lower triangular matrix of the items in this list. This matrix contains information about the support count of every 2-sequence candidate sequence that can be generated using items in the f-list, and is called S-Matrix |
| 4.2.2. PrefixSpan[Pei et al. 2001] . PrefixSpan examines only the prefix subsequences and projects only their corresponding postfix subsequences into projected databases. This way, sequential patterns are grown in each projected database by exploring only local frequent sequences. The key advantage of PrefixSpan is that it does not generate any candidates. It only counts the frequency of local items. It utilizes a divide-and-conquer framework by creating subsets of sequential patterns (i.e., projected databases) that can be further divided when necessary. PrefixSpan performs much better than both GSP and FreeSpan. The major cost of PrefixSpan is the construction of projected databases. |
| 4.2.3. WAP-mine [Pei et al. 2000] . Pattern-Growth Miner with Tree Projection. At the same time as FreeSpan and PrefixSpan in 2000/2001, another major contribution was made as a pattern growth and tree structure-mining technique, that is, is the WAP-mine algorithm [Pei et al. 2000] with its WAP-tree structure. Here the sequence database is scanned only twice to build the WAP-tree from frequent sequences along with their support, a “header table” is maintained to point at the first occurrence for each item in a frequent itemset, which is later tracked in a threaded way to mine the tree for frequent sequences, building on the suffix. The first scan of the database finds frequent 1sequences and the second scan builds the WAP-tree with only frequent subsequences. |
| 4.2.4. FS-Miner [El-Sayed et al. 2004] . Inspired by FP-tree [Han et al. 2000] and ISM [Parthasarathy et al. 1999], FSMiner is a tree projection pattern growth algorithm that resembles WAP-mine and supports incremental and interactive mining. The significance of FS-Miner is that it starts mining immediately with 2-subsequences from the second (which is also the last scan) of the database (at k = 2). It is able to do so due to the compressed representation in the FS-tree, which utilizes a header table of edges (referred to as links in El-Sayed at el. [2004]) rather than single nodes and items, compared to WAP-tree and PLWAP-tree. It is also considered a variation of a trie, as it stores support count in nodes as well as edges of the tree that represents 2-sequences and is required for the incremental mining process. |
4.3. Hybrid Algorithms
|
| Some algorithms combine several features that are characteristics of more than one of the three categories in the proposed taxonomy. For example, PLWAP [Lu and Ezeife 2003] combines tree projection and prefix growth features from pattern-growth category with a position-coded feature from the early-pruning category. All of these features are key characteristics of their respective categories, so we consider PLWAP as a pattern-growth/early-pruning hybrid algorithm. The ability of some algorithms to utilize a wide range of efficient features gives them an edge over other algorithms. It is also important to mention here that some features cannot be combined into one technique, such as, for example, “multiple scans of the database” and “tree projection;” since “tree projection” is used as an alternative in-memory database as does “support counting avoidance,” it cannot be combined with “multiple scans of the database”. |
| 4.3.1. SPADE [Zaki 2001] – Apriori-Based and Pattern-Growth Hybrid Miner. SPADE is a major contribution to the literature, and is still considered one of the benchmark sequential pattern-mining algorithms. It relies on the Lattice theory [Davey and Priestley 1990] to generate candidate sequences. This idea is borrowed from the incremental sequential mining algorithm ISM introduced earlier by Parthasarathy [1999]. SPADE discovers sequences of subsets of items, not just single item sequences as is the case with Apriori [Agrawal et al. 1993]; it also discovers sequences with arbitrary time gaps among items, and not just consecutive subsequences. SPADE relies on a lattice of frequent sequences generated by applying lattice theory on frequent sequences and their subsequences. SPADE works mainly in three steps, first finding frequent 1-sequences in an apriori-like way; and second, frequent 2-sequences. The third step traverses the lattice for support counting and enumeration of frequent sequences. The lattice can be traversed in either breadth-first or depth-first search. |
| 4.3.2. PLWAP[Ezeife and Lu 2005] – Pattern-Growth and Early-Pruning Hybrid Miner. PLWAP [Ezeife and Lu 2005] utilizes a binary code assignment algorithm to construct a preordered position-coded linked WAP-tree, where each node is assigned a binary code used during mining to determine which sequences are the suffix sequences of the last event and to find the next prefix for a mined suffix without having to reconstruct intermediate WAP-trees. |
WORK DONE ON SEQUENTIAL PATTERN MINING WITH A PROGRESSIVE DATABASE
|
A. A General Model for Sequential Pattern Mining with a Progressive Database
|
| Publication: IEEE Transactions On Knowledge And Data Engineering, Vol. 20, No. 9, September 2008. Authors: Jen-Wei Huang, Chi-Yao Tseng, Jian-Chih Ou, and Ming-Syan Chen, Fellow, IEEE. |
| In practice, users are usually more interested in the recent data than the old ones. To capture the dynamic nature of data addition and deletion, this paper present a general model of sequential pattern mining with a progressive database while the data in the database may be static, inserted, or deleted. In addition, we present a progressive algorithm Pisa, which stands for Progressive mIning of Sequential pAtterns, to progressively discover sequential patterns in defined time period of interest (POI). The POI is a sliding window continuously advancing as the time goes by. Pisa utilizes a progressive sequential tree to efficiently maintain the latest data sequences, discover the complete set of up-to-date sequential patterns, and delete obsolete data and patterns accordingly. |
B. Efficient Support Coupled Frequent Pattern Mining Over Progressive Database
|
| Publication: International journal of Database Management Systems(IJDMS),Vol.2,No.2,May 2010. Authors: Keshavamurthy B.N. , Mitesh Sharma and Durga Toshniwal. |
| The sequential pattern mining on progressive databases is relatively very new, in which we progressively discover the sequential patterns in period of interest. Period of interest is a sliding window continuously advancing as the time goes by. As the focus of sliding window changes , the new items are added to the dataset of interest and obsolete items are removed from it and become up to date. This papre proposed novel approach efficiently mines frequent sequential pattern coupled with support using progressive mining tree |
C. Hiding Co-occurring Sensitive Patterns in Progressive Databases
|
| Publication: PAIS „10, March 22, 2010, Lausanne, Switzerland. Copyright 2010 ACM. Authors: Amruta Mhatre Durga Toshniwal. |
| Sometimes although a particular pattern is not interesting, its co-occurrence with another pattern may reveal certain sensitive information. In this paper we present a novel technique to hide sensitive co-occurring sequential patterns. The proposed method works on progressive databases. Progressive databases are a generalized model of static, dynamic and incremental databases. The applicability of the method is also extended to suit these different types of databases. |
D. Sequential Pattern Mining With Multiple Minimum Supports in Progressive Databases
|
| Publication: International Journal of Database Management Systems ( IJDMS ) Vol.4, No.4, August 2012. Authors: K.M.V.Madan Kumar, P.V.S.Srinivas and C.Raghavendra Rao. |
| Although there may be lot of research work done on sequential pattern mining in static, incremental, progressive databases, the previous work do not fully concentrating on support issues. In this work we proposed a new approach which can be applied on any algorithm independent of that whether the particular algorithm may or may not use the process of generating the candidate sets for identifying the frequent item sets. The proposed algorithm will use the concept of “percentage of participation” instead of occurrence frequency for every possible combination of items or item sets. The concept of percentage of participation will be calculated based on the minimum support threshold for each item set. This paper present an algorithm MS DirApp, which stands for Multiple Support Direct Appending, which discovers sequential patterns in by considering different multiple minimum support threshold values for every possible combinations of item or item sets. |
E. Novel Tree based Approach for Mining Sequential Pattern in Progressive Database
|
| Publication: International Conference on Recent Trends in Computational Methods, Communication and Controls (ICON3C 2012) Proceedings published in International Journal of Computer Applications® (IJCA). Authors: S. Daniel Rajkumar,T.K.S. Rathish Babu,Dr. N. Sankar Ram. |
| The sequential pattern mining on progressive databases is comparatively very new, in which progressively find out the sequential patterns in time of interest. Time of interest is a sliding window which is continuously move forwards as the time goes by. As the focus of sliding window changes, the new items are added to the dataset of interest and obsolete items are removed from it and become up to date. Progressive databases have posed new challenges because of the following innate characteristics such as it should not only add new items to the existing database but also removes the obsolete items from the database. |
CONCLUSION
|
| This paper presents a classification of sequential pattern-mining algorithms, and shows that current algorithms in the area can be classified into three main categories, namely, apriori-based, pattern-growth, and early-pruning with a fourth category as a hybrid of the main three. A thorough discussion of 13 characteristic features of the four categories of algorithms, with an investigation of the different methods and techniques, is presented. This review of sequential pattern-mining algorithms in shows that the important heuristics employed include the following: using optimally sized data structure representations of the sequence database; early pruning of candidate sequences; mechanisms to reduce support counting; and maintaining a narrow search space. The quest for finding a reliable sequential pattern-mining algorithm should take these points into consideration. |
| The following requirements should be considered for a reliable sequential pattern-mining algorithm. First, a method must generate a search space that is as small as possible. Features that allow this include early candidate sequence pruning and search space partitioning. Sampling of the database and lossy compression (i.e., concise representation) can also be used to generate a smaller search space. Second, it is important to narrow the search process within the search space. An algorithm can have a narrow search procedure such as depth-first search. Third, methods other than tree projection should be investigated for finding reliable sequential pattern-mining techniques. After that this paper also describe the work done on sequential pattern mining with progressive database which is the current research area. |
Figures at a glance
|
 |
 |
 |
 |
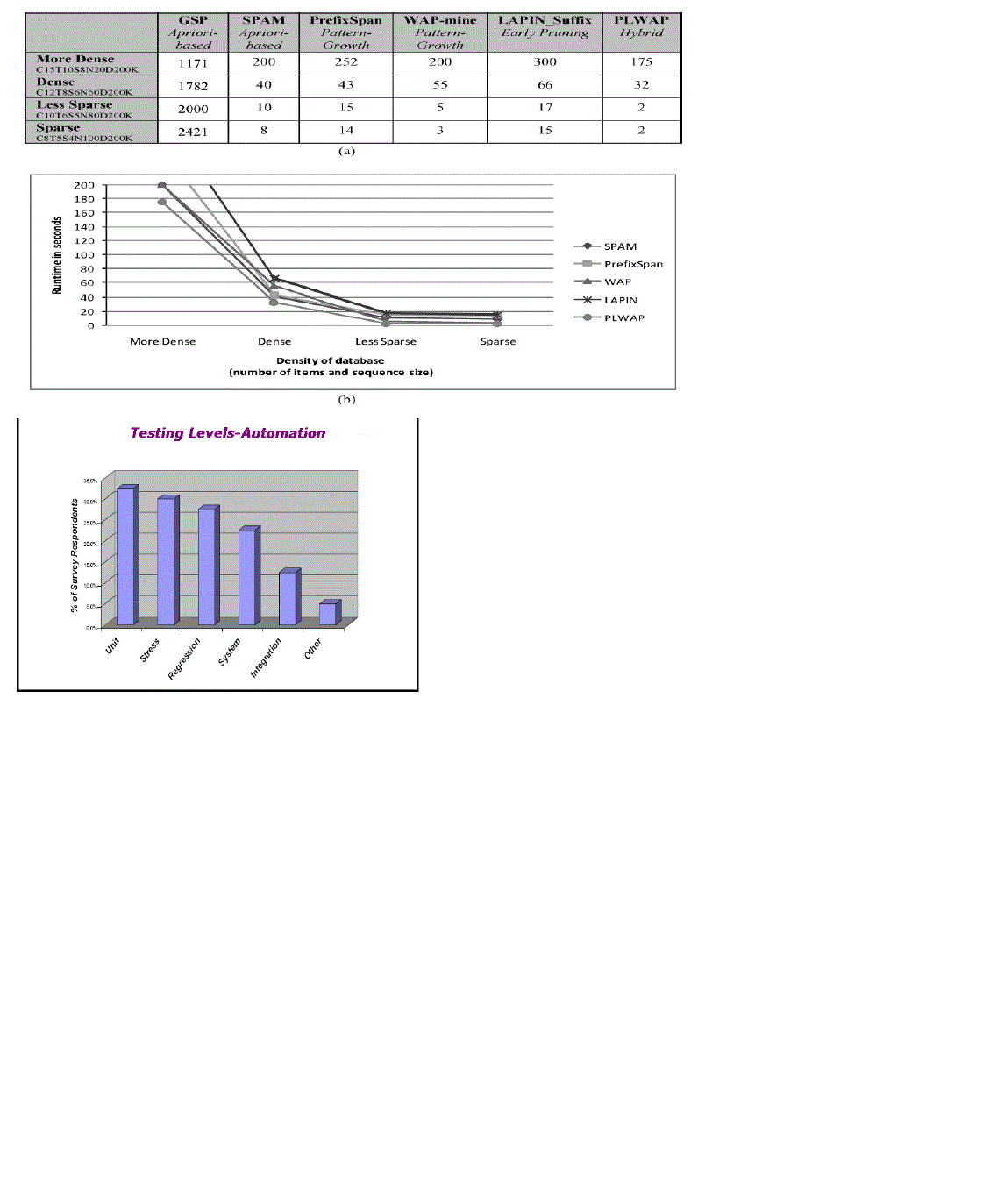 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
|
References
|
- AGRAWAL, R., IMIELINSKI, T., AND SWAMI, A. 1993. Mining association rules between sets of items in large databases. In Proceedingsof the ACM SIGMOD Conference on Management of Data. ACM, New York, 207–216.
- AGRAWAL, R. AND SRIKANT, R. 1994. Fast algorithms for mining association rules. In Proceedings of the1994 International Conference on Very Large Data Bases (VLDB’94). 487–499.
- AGRAWAL, R. AND SRIKANT, R. 1995. Mining sequential patterns. In Proceedings of the 11th Conference on Data Engineering (ICDE’95), 3–14.
- ANTUNES, C. AND OLIVEIRA, A. L. 2004. Sequential pattern mining algorithms: Trade-offs between speed and memory. In Proceedings of the Workshop on Mining Graphs, Trees and Sequences (MGTSECML/ PKDD ’04).
- AYRES, J., FLANNICK, J.,GEHRKE, J., AND YIU, T. 2002. Sequential pattern mining using a bitmap representation.InProceedings of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.429–435.
- BRIN, S.,MOTWANI, R., ULLMAN, J.D., AND TSUR, S. 1997. Dynamic itemset counting and implication rules for market basket analysis. In Proceedings of the ACM-SIGMOD International Conference on Management of Data (SIGMOD’97). ACM, New York, 255–264.
- CHIU, D.-Y., WU, Y.-H., AND CHEN, A. L. P. 2004. An efficient algorithm for mining frequent sequences by a new strategy without support counting. In Proceedings of the 20th International Conference on Data Engineering.375–386.
- DAVE, B. A. AND PRIESTLEY, H. A. 1990. Introduction to Lattices and Order.Cambridge University Press. DUNHAM, M. H. 2003. Data Mining: Introductory and Advanced Topics. Prentice Hall, Englewood Cliffs, NJ.EL-SAYED, M., RUIZ, C., AND RUNDENSTEINER, E. A. 2004. FS-Miner: Efficient and incremental mining of frequent sequence patterns in web logs. In Proceedings of the 6th Annual ACM International Workshop on Web Information and Data Management. ACM, New York, 128–135.
- EZEIFE, C. I. AND LU, Y. 2005. Mining web log sequential patterns with position coded pre-order linked WAP-tree. Int. J. Data MiningKnowl. Discovery 10, 5–38.
- EZEIFE, C. I., LU, Y., AND LIU, Y. 2005. PLWAP sequential mining: Open source code. In Proceedings of the 1st International Workshop on Open Source Data Mining: Frequent Pattern Mining Implementation (SIGKDD), ACM, New York, 26–35.
- FACCA, F. M. AND LANZI, P. L. 2003. Recent developments in web usage mining research. In Proceedings of the 5th International Conference on Data Warehousing and Knowledge Discovery. (DaWaK’03), Lecture Notes in Computer Science, Springer, Berlin. FACCA, F. M. AND LANZI, P. L. 2005. Mining interesting knowledge from weblogs: A survey. Data Knowl. Eng. 53, 3 225–241.
- GOETHALS, B. 2005. Frequent set mining. In The Data Mining and Knowledge Discovery Handbook, O. Maimon and L. Rokach Eds., Springer, Berlin, 377–397.
- HAN, J. AND FU, Y. 1995. Discovery of multiple-level association rules from large databases. In Proceedings of the International Conference on Very Large Data Bases (VLDB’95). 420–431.
- HAN, J., PEI, J.,MORTAZAVI-ASL, B.,CHEN, Q.,DAYAL, U., AND HSU,M.-C. 2000. Freespan: Frequent patternprojected sequential pattern mining. In Proceedings of the 6th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, New York, 355–359.
- HAN, J., PEI, J., AND YIN, Y. 2000. Mining frequent patterns without candidate generation. In Proceedings of the ACM SIGMOD International Conference on Management of Data (SIGMOD’00), ACM, New York, 1–12. HUANG, J.-W., TSENG, C.-Y., OU, J.-C., AND CHEN, M.-S. 2006. On progressive sequential pattern mining.InProceedings of the 15th ACM International Conference on Information and Knowledge Management.ACM, New York, 850–851.
- IV´ANCSY, R. AND VAJK, I. 2006. Frequent pattern mining in web log data.ActaPolytech.Hungarica 3, 1,- 77–90.
- JIN, X. 2006. Task-oriented modeling for the discovery of web user navigational patterns.Ph.D. dissertation, School of Computer Science. DePaul University, Chicago, IL.LIU, B. 2007.Web Data Mining: Exploring Hyperlinks, Contents, and Usage Data. Springer, Berlin.LU, Y. AND EZEIFE, C. I. 2003. Position coded pre-order linked WAP-tree for web log sequential pattern mining. In Proceedings of the 7th Pacific- Asia Conference on Knowledge Discovery and Data Mining.Lecture Notes in Computer Science, Springer, Berlin, 337–349.
- MASSEGLIA, F., PONCELET, O., AND CICCHETTI, R. 1999. An efficient algorithm for web usage mining.NetworkInform. Syst. J. 2, 571–603.
- MASSEGLIA, F., TEISSEIRE, M., AND PONCELET, P. 2005. Sequential pattern mining: A survey on issues and approaches. InEncyclopedia of Data Warehousing and Mining,1–14.
- NANDI, A. AND JAGADISH, H.V. 2007. Effective phrase prediction. In Proceedings of the International Conferenceon Very Large DataBases (VLDB’07).219–230.
- NANOPOULOS, A. AND MANOLOPOULOS, Y. 2000. Finding generalized path patterns for web log data mining. In Proceedings of theEast-European Conference on Advances in Databases and Information Systems.(Held jointly with the International Conference on DatabaseSystems for Advanced Applications: Current Issues in Databases and Information Systems, 215–228.
- PARK, J. S., CHEN, M. S., AND YU, P. S. 1995. An effective hash-based algorithm for mining association rules. In Proceedings of the 1995ACM-SIGMOD International Conference on Management of Data (SIGMOD’ 95). ACM, New York, 175–186.
- PARTHASARATHY, S., ZAKI, M.J., OGIHARA, M., AND DWARKADAS, S. 1999. Incremental and interactive sequence mining. InProceedings of the 8th International Conference on Information and Knowledge Management. ACM, New York, 251–258.
- PEI, J.,HAN, J.,MORTAZAVI-ASL, B., AND PINTO, H. 2001. PrefixSpan: Mining sequential patterns efficiently by prefix-projectedpattern growth. In Proceedings of the International Conference on Data Engineering.215–224.
- PEI, J.,HAN, J.,MORTAZAVI-ASL, B., AND ZHU, H. 2000. Mining access patterns efficiently from web logs. In Knowledge Discovery andData Mining.Current Issues and New Applications.Lecture Notes Computer Science, vol. 1805, Springer, Berlin, 396–407.-
- RYMON, R. 1992. Search through systematic set enumeration. In Proceedings of the 3rd International -Conference.on the Principles of Knowledge Representation and Reasoning.539–550.
- SAVASERE, A., OMIECINSKI, E., AND NAVATHE, S. 1995. An efficient algorithm for mining association rules in large databases. In Proceedings of the International Conference on Very Large Data Bases (VLDB’95).432–443.
- SONG, S., HU, H., AND JIN, S. 2005. HVSM: A new sequential pattern mining algorithm using bitmap representation. In Advanced Data Mining and Applications.Lecture Notes in Computer Science, vol. 3584, Springer, Berlin, 455–463.
- SRIKANT, R. AND AGRAWAL, R. 1996. Mining sequential patterns: Generalizations and performance improvements.InProceedings of the 5th International Conference on Extending Database Technology: Advances in Database Technology. Leture Notes in Computer Science, vol 1057, Springer, Berlin, 3–17.
- SRIVASTAVA, J., COOLEY, R., DESHPANDE, M., AND TAN, P.-N. 2000. Web usage mining: Discovery and applications of usage patterns from Web data. ACM SIGKDD Explorations Newsl. 1, 2, 12–23. TANASA, D. 2005. Web usage mining: contributions to intersites logs preprocessing and sequential pattern extraction with low support. Ph.D. dissertation, Universit´e De Nice Sophia-Antipolis. TOIVONEN H. 1996. Sampling large databases for association rules.In Proceedings of the International Conference on Very Large Data Bases (VLDB’95)134–145.
|