Keywords
|
| Binary arithmetic coding, M-coder, H.264/AVC. |
INTRODUCTION
|
| Arithmetic coding has attracted a growing attention in the past few years. It is an effective mode of coding and it is one of the very important algorithms in all image and video compression standards such as JPEG [1], JPEG-2000 [2] and H.264/AVC [3], HEVC [4], Dirac [5]. The algorithm is not only a lossless data compression method but also a type of entropy encoding. The arithmetic coder used in these standards which is multiplication free adaptive binary arithmetic coder with bit-renormalization and look-up tables used for multiplication approximation and probability estimation. |
| A basic idea about arithmetic coding uses a single floating point instead of string of input symbols so that it can be obtain a more efficient compression. The method is representing the encoded information as an interval between real axis of 0 ? .The interval is smaller than longer information, and indicating a longer information needs more number binary. |
| As a common requirement for all these applications, there is need for a fast and efficient binary arithmetic coding scheme. Efficient implementations in arithmetic coding both in hardware and software, however are not only required in the application domains of image and video coding but also in the data compression scheme needs high throughputs of arithmetic codes |
| The most efficient ABAC is the M-coder [7], which is the core of the context adaptive binary arithmetic coding (CABAC) [9] used in H.264/AVC. Since, M-coder is a key component of the entropy encoding in both compression schemes, the implementation of the ABAC with smaller memory foot print and lower computational complexity and higher compression efficiency remains an important challenge. |
RELATED WORK
|
| Arithmetic coding is a form of Entropy used in Lossless Data Compression. Normally, a string of characters such as the words "hello there" is represented using a fixed number of bits per character, as in the code. When a string is converted to arithmetic encoding, frequently used characters will be stored with fewer bits and not-so-frequently occurring characters will be stored with more bits, resulting in fewer bits used in total. Arithmetic coding differs from other forms of entropy encoding such as in that rather than separating the input into component symbols and replacing each with a code, arithmetic coding encodes the entire message into a single number, a fraction n where (0.0 ≤ n < 1.0). |
| What most compression systems have in common is the fact that the final process is entropy encoding, which is the process of representing information in the most compact form. It may be responsible for doing most of the compression work or it may just complement what has been accomplished by previous stages. When we consider all the different entropy coding methods, and their possible applications in compression applications, arithmetic coding stands out in terms of elegance, effectiveness and versatility, since it is able to work most efficiently in the largest number of circumstances and purposes. |
| Arithmetic coding is different from other coding methods for which we know the exact relationship between the coded symbols and the actual bits that are written to a file. It codes one data symbol at a time, and assigns to each symbol a real valued number of bits. |
| The code value v of a compressed data sequence is the real number with fractional digits equal to the sequence's symbols. We can convert sequences to code values by simply adding “0." to the beginning of a coded sequence, and then interpreting the result as a number in base-D notation, where D is the number of symbols in the coded sequence alphabet. For example, if a coding method generates the sequence of bits 0011000101100, then we have |
| Code sequence d = [0011000101100] |
| Code value v = 0: 00110001011002 = 0.19287109375 |
THE MAIN CONTRIBUTION OF THE PAPER
|
| In this paper, we present an efficient adaptive binary arithmetic coder which does not require multiplications and look-up tables. The proposed algorithm is a modification of ABAC based on virtual sliding window (VSW). It also allows assigning a specific window length depending on the statistical properties of the corresponding binary source. Therefore, in comparison to the state-of-the-art M-coder, it is faster and requires no look-up tables. Furthermore, it improves the compression efficiency. |
PROPOSED METHOD
|
A. Multiplication-free implementation:
|
| Probability estimation can be implemented by state machine approach. Some probability value is corresponds to each state. The transition state to state is defined by the value of the input symbol. This approach does not require multiplications or divisions for probability calculations. In addition to this the fixed set of states allows to implement the interval division part of the arithmetic coder without multiplications [6]. |
| For example let us consider a state machine based probability estimation in state-of-the-art M-coder from H.264/AVC standard. In M-coder [7] input symbols are divided in two types: Most probable symbols (MPS) and least probable symbols (LPS). State machine contains 64 states. East state defines probability estimation for least probable symbol. Set of probability values { ?p0,p?1,?p2......?p63 }. |
| To remove the multiplication, M-coder uses its approximation. After the renormalization procedure, register R satisfies the following inequality: |
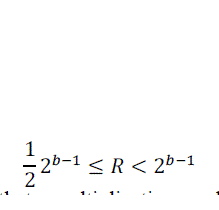 |
| From (1) it follows that a multiplication can be approximated in the following way |
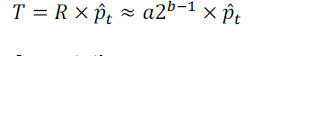 |
B. Look-up table implementation:
|
| probability estimation using virtual sliding window is proposed [10] |
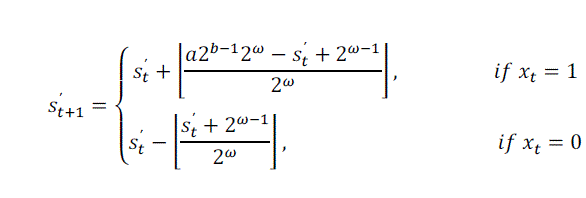 |
| In comparison with the M-coder, provides better compression efficiency due to an assignment of a specific virtual sliding window length selected according to the statistical properties of the corresponding binary source [10] and using multiplication in interval division part of the arithmetic coder instead of its approximation. Nevertheless, using these multiplications is not efficient; especially for a hardware implementation. |
| The proposed method gives the solution uses look-up table-free approach based on virtual sliding window (VSW). As an alternative to arithmetic coders, range coders use bytes as output bit stream element and do byte renormalization at a time. It was shown that adaptive binary range coder allows decreasing computation complexity. The new CABAC architecture was proposed. This architecture reduces the memory requirement by 50%, with at the expense of up to 0.02% coding loss. |
THE PROPOSED ADAPTIVE BINARY ARITHMETIC CODER
|
| To eliminate the multiplication operation, we use a similar reasoning as the one described in the above. Let us multiply both sides of above equation by α2b-1: |
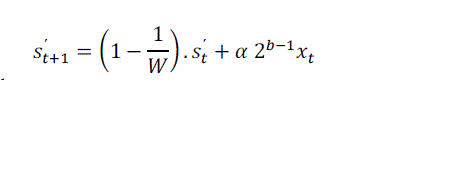 |
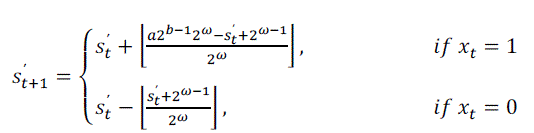 |
| Taking into account of equations (1), (2) |
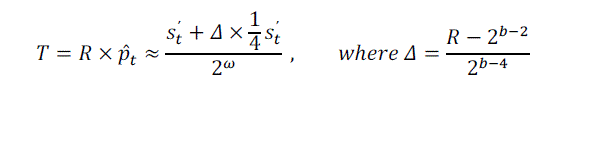 |
| The proposed coder can be implemented by using conditional and addition operations |
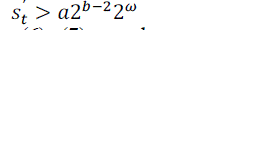 |
| By seeing the above equations (6), (7) an adaptive binary arithmetic coding is proposed by using conditional and addition operations. |
SIMULATION RESULTS
|
| For practical experiments the proposed adaptive binary arithmetic coder was embedded into the JM codec which is the reference software of H.264/AVC video coding standard. Compression results were obtained for the test video sequence “Pedestrian Area “for the Main profile of the standard. Bit-rate savings in percentage related to the M-coder for different quantization parameters are presented in Table 1. For both coders L and R are 10-bits registers (b = 10). |
| Our results show that the proposed adaptive binary arithmetic coder allows improving compression ratio of the H.264/AVC video coding standard for fixed visual quality. At the same time it has less encoding time than the Mcoder. |
CONCLUSION
|
| A new fast and efficient algorithm of binary arithmetic coding was presented. In comparison to the M-coder, it is faster, achieves better compression efficiency and less computational complexity and does not require look-up tables. Taking into account of these considerations the proposed coder is a modification of ABAC based on VSW. This coder can also achieve the trade-off between adaptation speed and precision of the probability estimation due to the utilization of different window sizes w. Experimental results have shown that our proposed coder provides advantages both in terms of compression performance and speed, when compared to the state-of-the-art M-coder. Therefore, the proposed ABAC can be more preferable for a future image and video coding standards and non-standardized codec’s. |
Tables at a glance
|
 |
| Table 1 |
|
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
References
|
- E. Belyaev, M. Gilmutdinov, and A. Turlikov, “Binary arithmetic coding system with adaptive probability estimation by Virtual
- D.arpe, H. Schwarz, and T. Wiegand, “Context-based adaptive binary arithmetic coding in the H.264/AVC video compression standard,” IEEE Trans. Circuits Syst. Video Technol., vol. 13, no. 7, pp. 620–636, Jul. 2003.
- V. Sze and M. Budagavi, “Overview of the high efficiency video coding (HEVC) standard,” IEEE Trans. Circuits Syst. Video Technol., vol. 22, no. 12, pp. 1649–1668, Dec. 2012.
- T. Nguyen, H. Schwarz, H. Kirchhoffer, D. Marpe, and T. Wiegand, “Improved context modeling for coding quantized transform coeffi- cients in video compression,” in Proc. Picture Coding Symp., 2010.
- H. Eeckhaut, B. Schrauwen, M. Christiaens, and J. Van Campenhout, “Tuning the M-coder to improve dirac’s entropy coding,” WSEAS Trans. Inf. Sci. Applicat., pp. 1563–1571, 2005.
- W.Pennebaker, J.Mitchel,G.Langdon,and R.Arps,“Anoverview of the basic principles of the q-coder adaptive binary arithmetic coder,” IBM J.Res. Develop., vol. 32, pp. 717–726, 1988.
- D. Marpe and T. Wiegand, “A highly efficient multiplication-free bi- nary arithmetic coder and its application in video coding,” in Proc. IEEEInt. Conf. Image Process., 2003, pp. 263–266.
- High Efficiency Video Coding, [Online]. Available: http://www.h265. net/
- V.SzeandM.Budagavi,“HighthroughputCABACentropycodingin HEVC,” IEEE Trans.CircuitsSyst.Video Technol.,vol.22,no.12,pp. 1778–1791,Dec. 2012.Sliding Window,” in Proc. 10th IEEE Int. Symp. Consumer Electron., 2006, pp. 194–198.
- D. Karwowski and M. Domanski, “Improved context-adaptive arithmetic coding in H.264/AVC,”in Proc.17th Eur.SignalProcess.Conf., 2009.
- D.arpe, H. Schwarz, and T. Wiegand, “Context-based adaptive binary arithmetic coding in the H.264/AVC video compression standard,”IEEETrans. Circuits Syst. Video Technol., vol. 13, no. 7, pp. 620–636, Jul. 2003.
- D. Karwowski and M. Domanski, “Improved context-adaptive arithmetic coding in H.264/AVC,”in Proc.17th Eur.SignalProcess.Conf., 2009.
- T. Nguyen, H. Schwarz, H. Kirchhoffer, D. Marpe, and T. Wiegand, “Improved context modeling for coding quantized transform coeffi- cientsin video compression,” in Proc. Picture Coding Symp., 2010.
- K.Vermeirsch,J.Barbarien,P.Lambert,andR.VandeWalle,“Region- adaptive probabilitymodel selection forthe arithmetic coding ofvideotexture,”in Proc. IEEE Int. Conf. Acoust., Speech, Signal Process., 2011, pp. 1537–1540.
- D. Hong and A. Eleftheriadis, “Memory-efficient semi-quasi renor- malization for arithmetic coding,” IEEE Trans. Circuits Syst. Video Technol., vol. 17, no. 1, pp. 106–109, Jan. 2007.
- M. Schindler, “Byte oriented arithmetic coding,” in Proc. Data Com- pression Conf., 1998.
- D.Subbotin, CarrylessRangecoder, 1999, [Online].Available:http://search.cpan.org/src/SALVA/Compress-PPMd-0.10/Coder.hpp.
- P. Lindstrom and M. Isenburg, “Fast and efficient compression of floating-point data,” IEEE Trans. Vis. Comput.Graphica, vol. 12, no. 5, pp.1245–1250, Sep.-Oct. 2006.
- A. Said, “Comparative analysis of arithmetic coding computational complexity,” Hewlett-Packard Lab. Rep., HPL-2004-75, 2004.
- K. Sarawadekar and S. Banerjee, “An efficient pass-parallel architec- ture for embedded block coder in JPEG 2000,” IEEE Trans. Circuits Syst. Video Technol., vol. 21, no. 6, pp. 825–836, Jun. 2011.
- “JPEG 2000 Image Coding System: Core Coding System,” ITU-T and ISO/IEC JTC 1, ITU-T Rec. T.800 and ISO/IEC 15444-1, JPEG 2000 Part 1, 2000
|