AN EFFICIENT APPROACH FOR THE
IMPLEMENTATION OF FP TREE

SADHANA KODALI; KAMALAKAR M; CH. GAYATRI; K.PRAVALLIKA

AN EFFICIENT APPROACH FOR THE IMPLEMENTATION OF FP TREE

SADHANA KODALI1, KAMALAKAR M2, CH. GAYATRI 3, K.PRAVALLIKA4

Assistant professor, Department of IT, Lendi institute of Engineering and Technology, Vizianagaram, AndhraPradesh,India
Assistant Professor, Department of CSE, Raghu Engineering College, Visakhapatnam, Andhra Pradesh,India
10KD1A1212, IV/IV B Tech, Department of IT, Lendi institute of Engineering and Technology, Andhra Pradesh, India
10KD1A1239, IV/IV B Tech, Department of IT, Lendi institute of Engineering and Technology, Andhra Pradesh, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Frequent pattern mining is one of the most common mining techniques to identify the frequent patterns in large data sets. The Apriori algorithm is one algorithm very efficient for mining frequent patterns. But the drawback is it generates a number of candidate item sets. The FP tree is a frequent pattern technique without candidate item set generation. We have proposed an approach for improving the performance of the FP tree using the parameter average support count.

Keywords

Frequent pattern mining, Apriori algorithm, FP tree, candidate item sets, average support count.

INTRODUCTION

Mining frequent patterns in transactional databases is a popular field of study in data mining. Apriori algorithm [1] is a traditional algorithm for finding the frequent patterns using some statistical measures such as support count and confidence. But the drawback of the Apriori algorithm is repeated database scanning and pruning of infrequent candidate item sets. Generating of the candidate item sets and pruning of the infrequent items is cost effective if large data sets are considered. An approach was proposed for mining frequent patterns without candidate generation [5] and an efficient FPtree based mining method, FP-growth was developed, for mining the complete set of frequent patterns by pattern fragment growth. [2].In our paper we would like to improve the efficiency of this algorithm by proposing an approach to still reduce the infrequent candidate generation and improve the space and time complexity of the algorithm. The algorithm efficient FP tree has the following major steps:

-Scan the database for the first pass and prune the item sets with infrequency using a threshold value avgsup. [3].

-Now the large database is condensed to a smaller data structure called the FP tree.

-Partitioning-based, divide-and-conquer method is used to decompose the mining task into a set of smaller tasks for mining confined patterns in conditional databases, which dramatically reduces the search space.

PROCESSING THE DATABASE

The first step is to preprocess the database before applying the algorithm. We take an example dataset to which we apply the formulas derived in [3].We compare this with the normal way of generating the fp tree and show the difference between these two approaches. We proposed a measure called as avgsup which is obtained by calculating the total support counts of n items and calculating the average of these items. This approach is much better for pruning of the infrequent items. The reason for this is, all the infrequent items fall below this threshold value called the avgsup. If there are {x1, x2, x3…. xk} items the avgsup is calculated using [3]

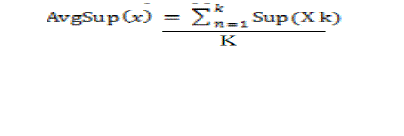The example dataset is taken in the following table:

The individual support counts of the items in the transaction are given in Table 2:

Step 1: Calculation of average support:

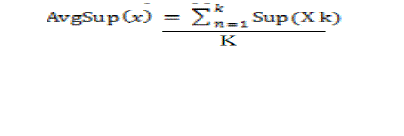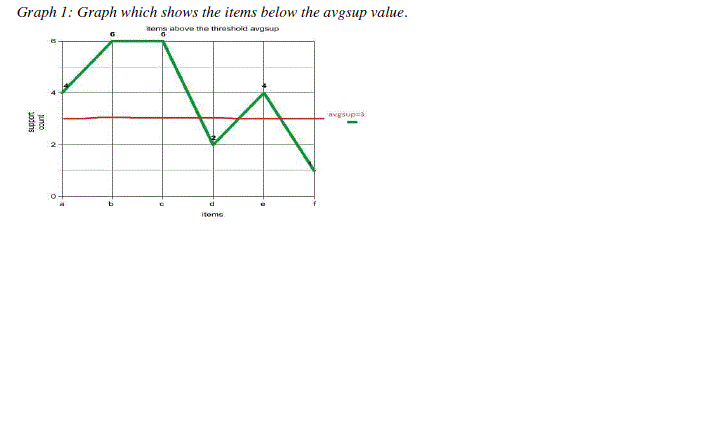
Avgsup= (4+6+6+2+4+1)/6

The support count of each item divided by the number of items. The value of avgsup for our example would be 3.5 for which we consider the floor value. The floor value of the avgsup denoted as ? avgsup?is given as 3.

Step-2: Pruning of the transactional database with avgsup count less than 3.We get the following items considered as the most frequent items

After removing the list of transactions which do not satisfy the threshold avgsup we get the above table.

CONSTRUCTION OF FP-TREE

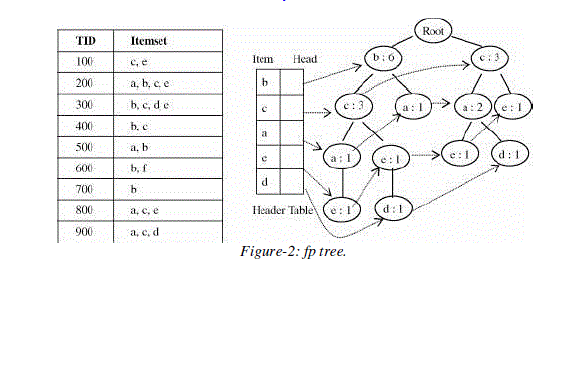
An fp tree is constructed for the items in Table 3 using the normal approach for the construction of fp tree.

The same data is used to normally generate the fp tree. Figure: 2 represents the normal way of construction of the fp tree [6].

Observing the tree in figure 1 we can say it is an optimal way of implementing the fp tree. The tree in figure 1 clearly reduces the space complexity when compared with the normal way of generating the fp tree.

From this we can understand that items d and f are infrequent and those item-sets with the infrequent items become less frequent and the elimination of such items from the transactional database for the construction of the fp tree will not affect the frequent pattern.

EFFICIENCY OF THE PROPOSED APPROACH

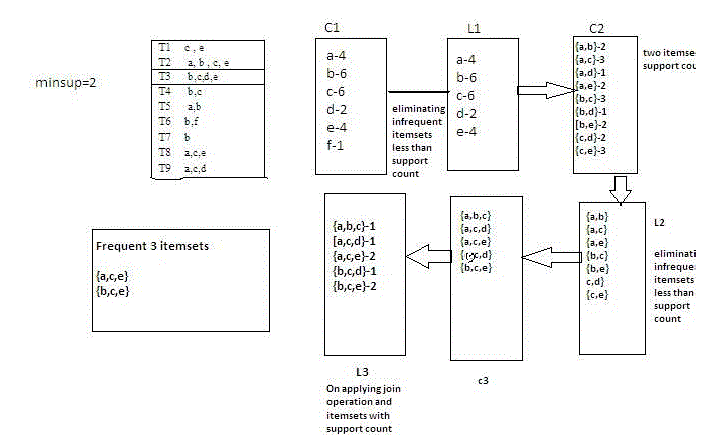
Using the same transactional database we apply Apriori algorithm and compare our results of the efficient fp tree with that of the existing Apriori algorithm.The apriori algorithm follows the steps below for the generation of frequent item-sets.

Step1: Apriori uses breadth-first search and a Hash tree structure to count candidate item sets efficiently. It generates candidate item sets of length k from item sets of length k-1.

Step2: Then it prunes the candidates which have an infrequent sub pattern. According to the downward closure lemma, the candidate set contains all frequent k-length item sets. [4]

Step3: After that, it scans the transaction database to determine frequent item sets among the candidates.

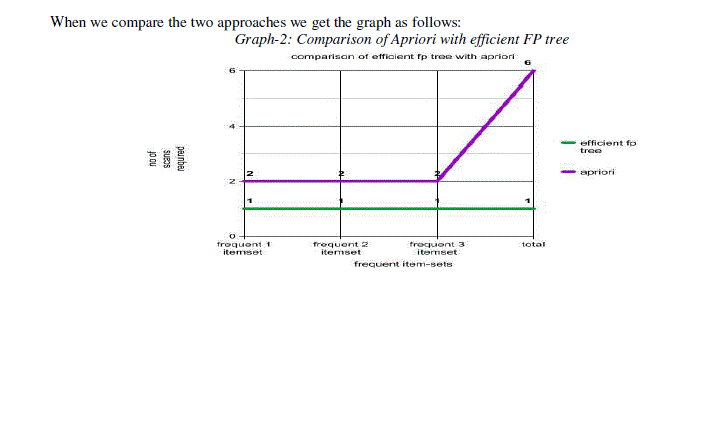
Observing the figure 1 and figure 3, we have the same frequent 3 item-sets. In our proposed approach efficient fp tree we obtained the frequent 3-item-sets only with one scan. But with the existing technique Apriori algorithm we need to scan the database four to five times and apply the pruning step to eliminate the infrequent item sets.

CONCLUSION

From the above we can observe that the efficiency of the proposed approach is more when compared with the existing techniques. The approach proposed by us will improve the time and space complexity. The approach proposed compresses the dataset and requires only one scan and two passes for the identification of frequent itemsets.

Tables at a glance


Table 1	Table 2	Table 3

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4	Figure 5

References

R. Agrawal and R. Srikant.“Fast algorithms for mining association rules in large databases.”Re-search Report RJ 9839, IBM Almaden Research Center, San Jose, California, June 1994.

JIAWEI HAN, JIAN PEI, YIWEN YIN, RUNYING MAO “Mining Frequent Patterns without Candidate Generation: A Frequent-Pattern Tree Approach “Proceedings of Data Mining and Knowledge Discovery, 8, 53–87, 2004 Kluwer Academic Publishers. Manufactured in The Netherlands.

Sadhanakodali,Kamalakar M ,”An Approach for Improving the Performance of the Apriori Algorithm published in IIJDWM”volume 3 issue 2.May2013.

en.wikipedia.org/wiki/Apriori_

Mining Frequent Patterns without Candidate Generation proceedings of SIGDOM ‘2000. Jiawei Han, Jian Pei, and Yiwen Yin.

C s n B e “An Implementation of the FPgrowth Algorithm “OSDM '05 Proceedings of the 1st international workshop on open source data mining: frequent pattern mining implementations.

/td>