An Efficient Contrast Enhancement Based On
Image Equalization with Improved Threshold
Median Filter

Nia Achu Issac; Anjaly Viswan

An Efficient Contrast Enhancement Based On Image Equalization with Improved Threshold Median Filter

Nia Achu Issac¹ and Anjaly Viswan²

M.Tech Student [VLSI & Embedded Systems], Sree Narayana Gurukulam College of Engineering Kadayiruppu, Kolenchery, Kerala, India
Asst. Prof, Department of Electronics and Communication, Sree Narayana Gurukulam College of Engineering, Kadayiruppu, Kolenchery, Kerala, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In this paper, a highly efficient contrast enhancement algorithm using Gaussian mixture modeling (GMM) is proposed for modeling the image gray level distribution. It gives better results compared to the existing algorithms .There are numerous enhancement techniques for contrast enhancement of which histogram equalization is mainly preferred due to its simplicity and effectiveness. The main limitations of this technique includes over enhancement and raised noise level. Hence this paper incorporates an enhancement criterion based on image equalization with improved threshold median filter which aims at enhancing the contrast along with suppression of impulse noise and preservation of edges .The proposed algorithm is adaptive and is free of parameter setting for a given dynamic range of soma in usa the enhanced image. It contributes effective enhancement and is applicable to both gray scale and color images.

Keywords

Contrast Enhancement, Histogram Equalization (HE), Gaussian mixture modeling (GMM), Histogram Partitioning, parameter estimation, Improved Threshold Median Filter (ITMF).

INTRODUCTION

The image enhancement aims to improve the interpretability of the information present in images for viewers. An enhancement algorithm is one that yields a better quality image by improving the image contrast. Image enhancement algorithms are employed to emphasize, sharpen or smoothen image features for display and analysis. Elementary enhancement techniques are mainly histogram based as they are simple, fast and produces acceptable results. Histogram modification basically modifies the histogram of an input image so as to improve the visual quality of the image. Histogram equalization is a process that attempts to spread out the gray levels in an image so that they are evenly distributed across their range. Normal histogram equalization usually leads to over enhanced output image with raised noise level.

Presently several methods are available for image enhancement such as HE [1], GHE [1], BPHEME [2], FHSABP [3], CEBGA [4] and HMF [5] etc. The aforementioned techniques may create problems when enhancing a sequence of images, when the histogram has spikes or when a natural-looking enhanced image is required.Image equalization using Gaussian mixture modelling also has been proposed for image enhancement [6]. It mainly uses Figuereudo Jain (FJ) algorithm for parameter estimation due to its advantages over EM algorithm [8].The main drawback of aforesaid method is in the modeling section, which is varying best models during successive modeling. Hence to overcome this, the concept of histogram equalization is proposed with improved GMM.In this enhanced image is generated by transforming the pixels gray levels in each input interval to the appropriate output gray-level interval according to the dominant Gaussian component and the cumulative distribution function of the input interval.

By enhancing the contrast of an image through transformation of its intensity levels, the histogram equalization might amplify noise if present and produce worse results. So there is need for filtering .This paper proposes an efficient contrast enhancement method based on image equalization with improved threshold median filter which eliminates the impulse noise and preserves the edges of the image. The proposed algorithm is adaptive and is free of parameter setting for a given dynamic range. This paper is organized as follows. Section II discusses the proposed methodology. Section III gives the simulation results and details. Conclusion and future enhancement is provided in Section IV .In this thesis for implementation of techniques MATLAB 12.a version is used which is a high-performance language for technical computing.

PROPOSED METHODOLOGY

Consider an input image X which has a dynamic range [xu, xl].The main objective of the algorithm is to generate an enhanced image Y within the range [yu, yl] which exhibits more visual quality than X.

The algorithm concentrates on the following steps:

A .Filtering

B. GMM Modeling

C. Histogram Partitioning

D. Mapping

A. Filtering

In digital signal and image processing; an image is often corrupted by noise in its acquisition or transmission. Noise is the undesirable information or signal which contaminates the image. The main goal of filtering is to enhance fine details in an image. Many conventional filtering techniques are used to eliminate the noise and to preserve the edges. Filtering techniques can be linear or non linear. The linear filtering leads to blurring and do not remove the noise effectively. Nonlinear filtering is generally preferred for removal of impulse noise and preservation of edges.

`The median filter is an effective method for the removal of impulse noise present in an image [11]. It replaces the central value in the concerned window with the median of all pixel values in it. The drawback of using standard median filter is that it fails to detect whether the pixel is noisy or not. So as it replaces both noisy and noise free pixels it leads to blurring of the image. The existing median filtering technique decreases the quality of the image rather than improving it. To overcome the above mentioned limitations modified forms of median filters have been proposed [12]. In this paper the Improved Threshold Median Filtering technique (ITMF) [13] is used to reduce the noise level in enhanced image and to preserve its edges. Thus this paper presents a new novel approach for image contrast enhancement using Image Equalization with Improved Threshold Median Filter. It is an adaptive 2D median filter. This median filter removes impulse noise by replacing the target pixel with the median value of all those pixels in the filtering window only if it is a noisy pixel. Here it uses two conditional thresholds (T_LOW, T_HIGH) to distinguish corrupted pixels from the noise-free pixels [13].The main advantage of this filter is that only corrupted pixels are replaced with the median values otherwise it is skipped. It is compared with other standard filters such as Min Filter, Max filter, Median filter, weighted average filter etc and it is noticed that this filter shows better results so it is chosen in our paper.

After filtering noise in the image is removed thereby the contrast may also get reduced. Thus after filtering our contrast enhancement algorithm has been applied to it so as to improve the contrast of the resultant output.

B.GMM Modeling

The histogram of the input image is modelled using GMM .A GMM can model any data distribution in terms of linear mixture of different Gaussian distributions with different parameters. Each Gaussian component has a different mean, standard deviation and weight in the mixture model ([6],[8]). Equation for finding GMM model is given by

where P(wn) is the probability of clusters ,N is the maximum number of clusters and p(x/wn) is the Gaussian density function.GMM is mainly specified by its parameters[8] .FJ algorithm is used for estimating the parameters of GMM due to its advantages over EM algorithm [8].This paper proposes a modified FJ algorithm for GMM. The main problem in existing algorithm is initialization of parameters. During each modeling process for the estimation of best parameters, the best model might change due to the random selection of mean values from the given set of data ([7]-[9]). The aforesaid problem is solved in this paper by diagonally selecting the mean values rather than selecting them randomly so as to make the modeling process more efficient. The main advantage of the proposed method is that during each modeling the best model obtained remains the same.

C. Histogram Partitioning

After the estimation of best model from the modeling section, the histogram is subjected to partitioning to get the input intervals. The intersection points of the Gaussian components are used for partitioning the dynamic range of the input image into several input gray-level intervals. The intersection points between two Gaussian components wp and wq are found by solving

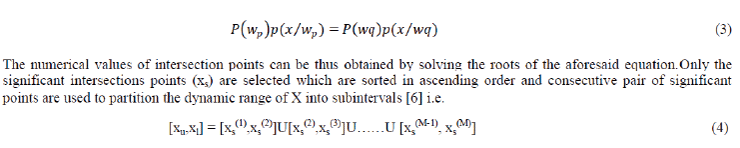Thus the dynamic range of input image is represented by the union of all intervals where M is the maximum number of significant intersection points. For each input gray level interval there is only one Gaussian component that is dominant with respect to the others which represents the data within that interval. Subinterval [xs (m), xs (m+1)] is represented by a Gaussian component(wm) , which is dominant with respect to the other Gaussian components in it. The dominant Gaussian component is found by considering the a posteriori probability of each component in specified interval.The cumulative distribution function (CDF) ([6] , [10]) in each input interval is also found by

D. Mapping

It is divided into the following sub sections:

1) Weighting section:

Each interval covers a certain range, which is proportional to weight α_m. Enhanced image is obtained by mapping each input interval to corresponding output interval by adding weight which depends on the rate of the total number of pixels that fall into interval and the standard deviation of the dominant Gaussian component[6]. Since the human eye is more sensitive to sudden changes in widely scattered data and less sensitive to smooth changes in densely scattered data, larger weights are given to widely scattered data and vice versa.

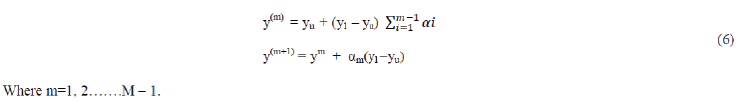2) Parameter estimation for final mapping:

The gray levels of the pixels in each input interval are transformed according to the dominant Gaussian component and the CDF of the interval to obtain the contrast-equalized image. For mapping, new parameters μ and of the dominant Gaussian component (wm ) of output interval have to be estimated [6] .The new parameters of the Gaussian distribution are computed as follows:

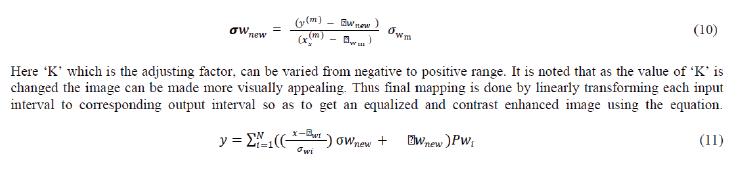SIMULATION RESULTS AND DISCUSSIONS

The original image and the enhanced image using the proposed method are shown here. Image equalization using GMM[6] has already being proved that it produces better enhancement results compared to other techniques like GHE [1], BPHEME [2], FHSABP [3], CEBGA [4] and HMF [5].Thus here in this paper we use images from fig 2 to fig 5 to compare the proposed method with HE[1] and Automatic Image Equalization And Contrast Enhancement Using GMM [6]. For experimental evaluation, Mat Lab 2012.a is used. For color images, the contrast enhancement is quantified by computing these measures on their luminance channel L*only. The input image is transformed to the CIE L*a*b* color space, and the luminance component L*is processed for contrast enhancement .From visual quality point of view, proposed algorithm is Comparable with existing systems. For the proposed method, the computed value of PSNR and MSE for different filters are shown in Fig.6, only few results are shown here. From the results obtained we conclude that the PSNR and MSE values of ITMF are better than other filters so we chose this in our paper.

CONCLUSION AND FUTURE WORK

This work is mainly concentrated on enhancing the contrast of an image. The proposed system can achieve image equalization that is good enough even under diverse illumination condition. The proposed algorithm produces good contrast enhancement results by utilizing the concept of histogram equalization. This algorithm can be applied to both gray scale and color images. Images with low contrast are automatically improved in terms of an increase in the dynamic range. Images with sufficiently high contrast are also improved but not as much. The algorithm further enhances the color quality of the input images in terms of color consistency. The proposed algorithm is free from parameter setting.

The current work is focused only on getting better enhancement by changing the value of adjusting factor ‟K‟. Thus as a future work this can be extended by evaluating the value of K automatically as per requirement of the image i.e. making K an adaptive factor.

ACKNOWLEDGEMENT

Authors would like to thank all the researchers who have contributed in this field of research. The comments of anonymous reviewers to improve the quality of this paper are also acknowledged.

Figures at a glance


Figure 1	Figure 2	Figure 3

Figure 4	Figure 5	Figure 6

References

R. C. Gonzalez and R. E. Woods, Digital Image Processing. Upper Saddle River, NJ: Prentice-Hall, 2006.

C.Wang and Z.Ye, “Brightness preserving histogram equalization with maximum entropy: A variation perspective,” IEEE Trans. Consum. Electron., vol. 51, no. 4, pp. 1326–1334, Nov. 2005.

C. Wang, J. Peng, and Z. Ye, “Flattest histogram specification with accurate brightness preservation,” IET Image Process., vol. 2, no. 5, pp. 249–262, Oct. 2008.

T. Arici, S. Dikbas, and Y. Altunbasak, “A histogram modification framework and its application for image contrast enhancement,” IEEE Trans. Image Process., vol. 18, no . 9, pp. 1921–1935, Sep. 2009.

S. Hashemi, S. Kiani, N. Noroozi, and M. E. Moghaddam, “An image contrast enhancement method based on genetic algorithm,” Pattern Recognit. Lett., vol. 31, no. 13, pp. 1816–1824, Oct. 2010.

“Automatic Image Equalization And Contrast Enhancement Using Gaussian Mixture Modeling”: TurgayCelik and TardiTjahjadi, IEEE transactions on image processing, vol. 21, no. 1, january 2012

D. Reynolds and R. Rose, “Robust text-independent speaker identification using Gaussian mixture speaker models,” IEEE Trans. SpeechAudio Process., vol. 3, no. 1, pp. 72–83, Jan. 1995.

M. Figueiredo and A. Jain, “Unsupervised learning of finite mixture models,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 24, no. 3, pp.381–396, Mar. 2002

“Gaussian Mixture Modeling of Histograms for Contrast Enhancement”, Yu-Ren Lai, Kuo-Liang Chung Guei-Yin Lin, Chyou-Hwa Chen

M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York:Dover, 1965.

P.Jagaatheeswari, S.Sureshkumar and M.Rajaram,A novel approach for contrast enhancement based on histogram equalization followed by median filter,APRN.,vol. 4,no. 7, pp.41-45, Sep 2009

Rajoopandey,An improved switching median filter for uniformly distributed impulse noise removal, World Academy of Science. pp.349-351., 2008.

A Low-Complexity and Low Power Median Filter Design ,Takeaki Matsubara, Vasily G. Moshnyaga, and Koji Hashimoto, 2010 International Symposium on Intelligent Signal Processing and Communication Systems (lSPACS 2010) December 6-8,2010