An Enhanced Image Steganographic Method with High Payload Capacity using Multidirectional Block Based Pixel-Value Differencing

Abstract

To increase the payload capacity of the hidden secret information and to provide an imperceptible stego-image for human vision, an enhanced steganographic method using multidirectional block based pixel-value differencing is proposed in this paper.To enhance the hiding payload capacity in image an steganographic method based on three-pixel block differences by Lin and Hseuh referring to only one direction but in the proposed method multi directional edges are considered and effectively adopted to design the scheme of multi directional block based PVD.As we know our human vision is sensitive to slight changes in the smooth regions, while it can tolerate more severe changes in the edge regions, in proposed method more secret data is embedded in those busy regions.In addition, to reduce the quality distortion of stegoimage brought from setting larger embedding capacity, an optimal approach of selecting the reference point and adaptive rules are presented. This approach can be apply to gray as well as colored image also.Experimental results show that the proposed scheme can provide higher embedding capacity and give protection from dual statistical stego-analysis.Besides, the embedded confidential data can be extracted from stego-images without the need of original images.

Keywords

Steganography,Pixel-value differencing, Data hiding,Multidirectional,Block based.

INTRODUCTION

The Internet allows users to exchange information without the limitations of time and location. Unauthorized persons can easily obtain secret data if appropriate precautions are not taken.Although encrypting a message before transmitting it on the Internet may provide a safe way for secret communication, encryption systems, such as data encryption standard DES and RSA, encrypt a message by transforming it into a meaningless form, which may alert interceptors.Data hiding is a technique that imperceptibly hides secret data into cover media, such as digital images, videos, audios, etc. The cover medium is only slightly modified, so these changes do not arouse suspicion in potential interceptors who might then notice the secret data. an ideal steganography scheme, to keep the stego-image from drawing attention from the opponent, should maintain an imperceptible stego-image quality. That is to say, if there are more similarities between the cover image and the stego-image, it will be harder for an attacker to find out that the stego-image.For the past decade, many steganographic techniques for still images have been presented. A simple and well known approach is directly hiding secret data into the least-significant bit (LSB) of each pixel in an image has important secret data hidden inside it (Wu and Hwang, 2007). This way, the secret data is more likely to travel from the sender to the receiver safe and sound. Fridrich et al. [3,4] compressed the least significant bit (LSB) plane to obtain extra space for embedding secret data. Celik et al. [9] improved Fridrich et al.`s scheme and proposed the generalized- LSB (G-LSB) scheme by compressing the quantization residuals of pixels to obtain extra space for embedding a message. In the above two schemes, the payload capacity is highly related to the compressed results. Tian [5] used a technique of expanding the difference between two neighboring pixels to find redundant space for embedding a message. In his scheme, a large location map is required to determine whether a pair of pixels embeds a message. Alattar [6] used the difference expansion of a vector to obtain more embedding space. The pixel-value differencing (PVD) method proposed by Wu and Tsai [7] can successfully provide both high embedding capacity and outstanding imperceptibility for the stego-image.Wang and Huang[8] modify the basic PVD method and suggest that the remainder of the two consecutive pixels can be computed by using the modulus operation, and then secret data can be embedded into the two pixels by modifying their remainder.Mandal and Das[14] proposed an approach in which PVD method is used and check whether the pixel value exceeds the range on embedding. Positions where the pixel exceeds boundary has been marked and a delicate handle is used to keep the value within the range.Exploiting Tian`s scheme of difference expansion, Chang and Lu [10] calculated the difference between a pixel and the mean value of its neighboring pixels to embed a message. Although the hiding ability was improved, a large location map was still required in both Alattar`s and Chang and Lu`s schemes. Ni et al. [11] proposed a novel reversible data hiding algorithm based on shifting an image histogram. The maximum point of the histogram is selected to embed a message. When embedding a message into the image, the pixel value at the maximum point is altered by 1 or left unchanged if the message bit is “1” or “0”, respectively. However, few images contain a large number of pixels with equal pixel values, so the embedding capacity of Ni et al.`s algorithm is small. Chih-Chiang Lee and Yen-Ping Chu[13] proposed a scheme which is built upon is block-based centralized difference expansion. In the proposed scheme, the original cover image is partitioned into a series of non-overlapping blocks, and the payload of each block depends on its block size and the image complexity. A new method is employed to compute the image complexity of each image block, and all the blocks are classified into four levels according to their block complexity values, and finally different amounts of data are assigned to image blocks at different complexity levels.Ching-Chiuan Lin and Nien-Lin Hsueh[12] proposed a novel steganographic scheme based on three-pixel block differences in which it embeds a message into a cover image using the two differences between the first and the second pixel as well as between the second and the third pixel in a three-pixel block and in the cover image, an absolute difference between a pair of pixels is selected to embed the message if the number of pixel pairs with the difference in the image is the largest. To embed a bit “1” or “0”, the selected difference is increased by 1 or left unchanged, respectively.However this scheme does not provide high payload capacity of image and the qulity of stego image is not good enough.

In this paper we modify and enhance Ching-Chiuan Lin and Nien-Lin Hsueh`s algorithm where data hiding take place on the basis of taking difference between three pixel to only one direction,we considered multi directional edges and effectively adopted to design the scheme of multi directional block based PVD. Also, to reduce the quality distortion of the stego-image brought from setting larger embedding capacity, an optimal approach of selecting the reference point and adaptive rules are presented.This can maintain the stego-image at an acceptable and satisfied quality. The rest of this paper is organized as follows. Section 2 reviews the PVD method and Ching-Chiuan Lin , Nien- Lin Hsueh`s method. In Section 3, the proposed construction scheme is presented. Experimental results are illustrated and discussed in Section 4, prior to Conclusions in Section 5.

II(A) Review Of The Ching-Chiuan Lin and Nien-Lin Hsueh`s method

In this scheme, a three-pixel block in an image contains two absolute differences—the difference between pixels one and two, and the difference between pixels two and three. Such a difference is called block difference. For simplicity,difference and block difference are interchangeable.

An image is divided into non-overlapping three-pixel blocks, where the maximum and minimum allowable pixel values are 255 and 0, respectively. Let g(d) be the number of pixel pairs with absolute difference equal to d, where 0≤ d ≤ 253 and pixel pairs in the block which contains a pixel value equal to 0 or 255 are not considered when calculating g(d). Before embedding a message, the proposed scheme selects a pair of differences M and m such that g(M) ≥ g(M) and g(m) ≤ g(m_) for all 0≤ M , m_≤ 253. Let (bi0, bi1, bi2) denote a block i with pixel values equal to bi0, bi1, and bi2, and max(bi0, bi1, bi2) and min(bi0, bi1, bi2) denote the maximum and minimum pixel values in the block, respectively. First, blocks satisfying the following two conditions are selected:

(1) 1 ≤ bi0, bi1, bi2≤ 254;

(2) min(bi0, bi1, bi2)=1 or max(bi0, bi1, bi2)=254. For each selected block i, the sender performs the following actions:

(1) increase di0 by 1 if M + 1≤ di0≤ m − 1, and increase

di1 by 1 if M + 1≤di1≤m − 1, where di0 = |bi0 – bi1| and

di1=|bi1−bi2|;

2) embed a message into block i if di0=M or di1=M; (3) after performing actions (1) and (2), record the index of block i as overhead information if min(bi0, bi1, bi2)=0 or max(bi0, bi1, bi2) = 255.

For example, if M = 1 and m = 20, then blocks (2, 1, 2),

(253, 254, 240), and (246, 243, 254) are selected in this step. The resulting blocks will be: (2, 0, 2) if it embeds two bits “11”, (253, 254, 239) if it embeds a bit “0”, and (246, 242, 254). Note that the results of block (246, 243, 254) are not determined by the embedded message, since it cannot embed a message. On the other hand, blocks (0, 3, 5) and (3, 4, 6) are not selected in this step. In this example, the index of resulting block (2, 0, 2) will be recorded as overhead information.Note that block (2, 0, 2) embeds two bits “11” and only the central pixel is modified by 1. Then, the sender scans the image again and performs the following actions for each block i with 2≤ bi0, bi1, bi2≤ 253:

(1) increase di0 by 1 if M+1≤ di0≤ m−1, and increase di1 by 1 if M + 1≤ di1≤ m − 1;

(2) embed the overhead information and the residual message into block i if di0 = M or di1 = M. In the above example, block (3, 4, 6) will become (3, 4, 7) if it embeds a bit “0”. Obviously, the resulting blocks (2, 0, 2), (253, 254, 239), and (246, 242, 254) are not considered.

Given M and m, for each block i with 1≤ bi0, bi1, bi2≤ 254, the receiver performs the following actions: (1) extract the overhead information or a message if di0 ∈ {M,M + 1} or di1 ∈ {M,M +1}; (2) decrease di0 by 1 if M +2≤ di0≤m, and decrease di1 by 1 if M + 2≤ di1≤m. Then, the receiver extracts the remaining message and recovers original blocks from the blocks with block indexes recorded in the overhead information extracted in the above extraction process.

II(B) Review Of The Pvd Method

In the original PVD method [7], a gray-valued cover image is partitioned into non-overlapping blocks composed with two consecutive pixels, pi and pi+1. From each block, a difference value di can be calculated by subtracting pi from pi+1. The set of all difference values ought to range from −255 to 255. Therefore, di ranges from 0 to 255. Thus, the block with a small value di locates in the smooth area, whereas a block with a large value di is considered as a block with sharp edges. According to the properties of human vision, eyes can tolerate more changes in sharp-edge blocks than in smooth blocks. That is, more data can be embedded into the edge areas than into smooth areas. Therefore, in the PVD method, the first step is to design a range table with n contiguous ranges ( Rk where k = 1, 2,…,n ) and the table range is from 0 to 255. The lower and upper boundary of Rk are denoted by lk and uk, respectively, then Rk ∈[lk,, uk].The width wk of Rk is calculated by wk = uk – lk +1 and wk decides how many bits can be hidden in two consecutive pixels. Since Rk is designed as a variable, the original range table is required to extract the embedded secret data based on the consideration of security.

The embedding algorithm is described as follows:

1.Calculate the difference value di between two consecutive pixels pi and pi+1 for each block in the cover image. The value is given by di= pi+1- pi.

2.Using |di| to locate a suitable Rk in the designed range table, that is to compute j=mink(uk-|di|)where uk ≥|di| for all 1≤k≤n.Then Rj is the located range.

3.Compute the amount of secret data bits t that can be embedded in each pair of two consecutive pixels by Rj The value t can be estimated from the width wj of Rj this can be defined by t= ⎣ log2wj⎦.

4. Read t bits from the binary secret data and transform the bit sequence into a decimal value b . For instance, if bit sequence=110 , then the converted value b =6 .

5. Calculate the new difference value di` given by di` = lj + b if di>0 and di′ = − (lj + b),if di < 0 to replace the original difference di

6. Modify the values of pi and pi+1 by the following formula:

( pi`, pi+1` )=(pi - ⎣ m/2⎦, pi+1+⎣ m/2⎦ )

Where m=di`-di.Until now, to embed the secret data into the pixel pair ( pi`, pi+1` ) is done by changing the values of pi and pi+1.

Repeat Step 1-6 until all secret data are embedded into the cover image, then the stego-image is obtained. During the phase of secret extraction, the original designed range table is required. In the beginning, the same method in the embedding phase is used to partition the stego-image into pixel pairs (blocks). Then the difference value di` for each pair of two consecutive pixels p^ i and p^ i+1 in the stego-image is calculated. Next, is used to locate the suitable Rj in Step 2 during the di`embedding phase. Therefore, b` is obtained by subtracting lj from di` If the stego image is not altered, b` is equal to b . Finally, b` is transformed from a decimal value into a binary sequence with t bits, where t= ⎣ log2wj⎦.

III. THE PROPOSED METHOD

In the Ching-Chiuan Lin and Nien-Lin Hsueh`s method three horizontal and consecutive pixels can only represent a vertical edge, but the edge can have different directions. This motivates us to improve the method based on three-pixel block differences by considering three directions.

A. The Block Creation procedure

Normally, the edges in an image are roughly classified into vertical, horizontal, and two kinds of diagonal directions. Motivated from the classical PVD method and one proposed by Ching-Chiuan Lin and Nien-Lin Hsueh, using pixel pairs on one directional edge can work efficiently for information hiding. This should accomplish more efficiency while considering four directions from four two-pixel pairs. This can be implemented by dividing the image into 2×2 blocks and one example block is shown in Fig. 1. However, since the changing of pixel values for the fourth pixel pair affects the first and the second pairs, the fourth pair is useless and has to be discarded. Therefore, we propose that three pairs are used to embed the secret data. Before introducing the proposed algorithm, the block creation procedure is to partition the cover image into non-overlapping 2×2 blocks with 4 pixels.

B.The Multidirectional Block Based Pixel Value Differencing Scheme

As shown in Fig.1 each 2×2 block includes four pixels of p(x,y) p(x+1,y ) p(x,y+1) and p(x+1,y+1) where x and y are the pixel location in the image. Let p( x, y) be the starting point, then three pixel pairs can be found by grouping p( x, y) with the right, the lower, and the lower right neighboring pixels. Those three pairs are named by P0 , P1, and P2 where P0=( p(x,y) , p(x+1,y )), P1=( p(x,y) , p(x,y+1 )) and P2=( p(x,y) p(x+1,y+1 )) respectively.

When using the proposed Multidirectional Block Based Pixel Value Differencing Scheme to embed the secret data, each pair has it`s modified Pi`and a new difference value di′for i = 0,1,2 . Here, the detailed embedding algorithm is left to be described in Section 3.D. Now, the new pixel values in each pair are different from their original ones. That is, we have three different values for the starting point p(x,y) named p0`(x,y) , p1`(x,y) and p2`(x,y) from P0 , P1, and P2 , respectively. However, only one value for pi( x, y)` can exist after finishing the embedding procedures. Therefore, one of p`i(x+y) is selected as the reference point to offset the other two pixel values. That is, two pixel values of one pair are used to adjust the other two pairs and construct a new 2×2 block. Suppose that the reference point is pi( x, y) `, then the other two difference values, d0`and d2`, can be proven unchanged after the adjustment given by

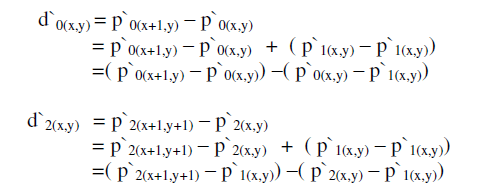Note that the embedded secret data are unaffected because of those three difference values are unaltered

C.Optimal Selection Rules for the Reference Point

Selecting different reference points results in varied Distort on to the stego-image. Here, we propose an optimal selection approach to achieve minimum Mean- Square-Error (MSE). Suppose that mi =di′− di , di and d`i are the difference values of pixel pair i before and after embedding procedures. The rules that can exactly determine one optimal reference pair without really estimating MSE are introduced as follows.

1) If all values of mi are great than 1 or smaller than -1, the optimal pixel pair ioptimal is the pair with the greatest |m| . For example, if mi={- 8, - 4, - 3}, i ∈{0,1, 2}, then ioptimal =0.

2) If all mi have the same sign and only one mi ∈{0,1, -1}, then the optimal pixel pair ioptimal is selected from the other two pairs with the smallest m . For example, if, mi ={4,3,1} i∈{0,1, 2}, then ioptimal =1.

3) If only one mi has a different sign from the other two pairs, the optimal pixel pair ioptimal is selected from the other two pairs with the smallest m . For example, if mi ={7, - 4,3}, i ∈{0,1, 2} , then ioptimal =2.

4) If only one mi ∈{0,1, -1} and the other two mi has different signs, the optimal pixel pair ioptimal is the pair with mi ∈{0,1, -1}. For example,if mi = {0, -4, 2},i∈{0,1, 2} , then ioptimal=0.

5) If there exists more than one pair with mi ∈{0,1, -1}, the optimal pixel pair ioptimal can be selected as any one pair with mi ∈{0,1, -1}. For example, if mi ={4,0,0}, i ∈{0,1, 2} then ioptimal=1 or 2.

By those selection rules described above, we can skip the calculation steps of MSE estimation to obtain the optimal reference pairs. Thus, the total computational complexity can be greatly reduced.

D. The Embedding Algorithm

The details of data hiding steps are described as follows.

1) Calculate four difference values di(x,y) for four pixel pairs in each block given by

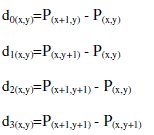2) Using |di,(x,y)| (i =0,…,3) to locate a suitable Rk,i in the designed range table, that is to compute j=mink(uk,j-|di,(x,y)|) where uk,j ≥|di,(x,y)| for all 1≤k ≤n. Then the located range can be represented by R j,i.

3) Compute the amount of secret data bits t i that can be embedded in each pair by Rj,i . The value t i can be estimated from the width w j,i of R j,i , this can be defined by t= [log2w j i ]

4) Read t i bits from the binary secret data and transform the bit sequence into a decimal value b i .

5) Calculate the new difference value d`i(x,y) given by d`i =li,j+ bi if di(x,y) ≥0 or d`i =-(li,j+ bi ) if di(x,y) <0 to replace the original difference d i(x,y) .

6) Modify the values of p n and p n + 1 by the following formula:

where pn and pn+1 represent two pixels in Pi and m=dn′ − dn .Until now, to embed the secret data into the pixel pair (pn`, pn+1`) is done by changing the values of p n and pn+1.

7)Using the selection rules to choose the optimal reference point p′i(x,y) with minimum MSE, then this selected point is used to offset the other two pixel pairs.

8) Now, the new block constructed from all pixel pairs and embedded with secret data is generated.

E. The Extraction Algorithm

To retrieve the embedded secret data from the stegoimage,the extraction algorithm is described in the following steps.

1) Partition the stego-image into 2×2 pixel blocks, and the partition order is the same as that in the embedding stage.

2) Calculate the difference values di`(x,y) separately for each block in the stego-image given by

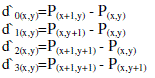3) |d`i(x,y)| is used to locate the suitable R k ,i as introduced in Step 2 of the embedding phase. At the same time, the amount of embedding bits t i, where ti = [log2 wj,i] is obtained.

4) After R k ,i is located, l j,i is subtracted from the selected |d`i(x,y)| and b`i is obtained. If the stego- image is not altered, is equal to bi . Finally,b`i is converted from a decimal value into a binary sequence with ti bits where ti = ⎣log2 wj,i⎦ . Note that the t i bit stream is only one part of the secret data before embedding.

IV. EXPERIMENTAL RESULTS

To demonstrate the accomplished performance of our proposed approach in capacity and security for hiding secret data in the stego-image, In our experiments, eight gray cover images ``Lena`` ,``Peppers```“Boat``, “Airplane”,`Baboon``, ”Tank”, ”Couple” and “Elaine”, were used, each with size 512 x512 to compare the proposed approach with the existing methods.

A. Capacity and PSNR

The secret binary data taken from the whole text of abstract part of this papers which is aproximately 1,271 bytes. We set the designed range table with the width in the set of wk={8,8,16,32,64,128}.The size of all cover images is 512×512 . Here, PSNR value is utilized to evaluate the invisibility of the stego-images.Table-I shows the experimental results of perfomance of the proposed method that demonstrate the proposed method enhances the data payload capacity of the images. To compare the proposed approach with the existing methods, Table II lists the experimental results after the secret data is embedded using those four approaches including proposed method.The hiding capacity (in bytes) and PSNR values achieved by the proposed scheme and the existing methods for seven images are shown. The listed values are the average results after embedding 100 randomly generated bit-sequences into the cover images.The results shows that the proposed approach can provide a higher performance in increasing the data payload capacity of the stego-images and maintaining the imperceptible quality simultaneously.

V. CONCLUSION

Using multidirectional edges we can hide more secret data into the cover image than the PVD and Ching- Chiuan Lin and Nien-Lin Hsueh`s method. Since our human vision is sensitive to slight changes in the smooth regions, while it can tolerate more severe changes in the edge regions, in proposed method more secret data is embedded in those busy regions.Also, we have presented an optimal selection approach for the reference point to reduce the quality distortion of the stego-image. This approach can be apply to gray as well as colored image also.Experimental results demonstrate that the secret data embedded in the stego image is imperceptible for human vision while compared with the cover image.Furthermore, the proposed approach can achieve superior embedding capacity than the existing methods, from the experimental results.Also, the extraction of the embedded secret data can work correctly from stegoimages without the need of original cover images. This has shown multiple merits of the proposed technique for data hiding.

Tables at a glance

Table 1 Table 2 Table 3

Figures at a glance

Figure 1 Figure 2

References

1. F. A. P. Petitcolas, R. J. Anderson and M. G. Kuhn, “Information Hiding - a Survey,” Proceedings of the IEEE, Vol. 87, pp. 1062–1078, (1999)
2. Y. K. Lee, L. H. Chen, “High capacity image steganographic model,” IEE Proceedings on Vision, Image and Signal Processing, Vol. 147, No.3, pp. 288-294, (2000)
3. J. Fridrich, M. Goljan, and R. Du, “Detecting LSB steganography in color, and gray-scale images,” IEEE multimedia, Vol. 8, Issue 4, pp. 22-28, (2001)
4. J. Fridrich, M. Goljan, R. Du, Lossless data embedding—new paradigm in digital watermarking, EURASIP J. Appl. Signal Process. 2002 (2) 185–196, (2002)
5. J. Tian, Reversible data embedding using a difference expansion, IEEE Trans. Circuits Syst. Video Technol. 13 (8) 890–896, (2003)
6. A.M. Alattar, Reversible watermark using the difference expansion of a generalized integer transform, IEEE Trans. Image Process. 13 (8) 1147– 1156, (2004)
7. H.-C. Wu, N.-I. Wu, C.-S. Tsai, and M.-S. Hwang, “Image steganographic scheme based on pixel-value differencing and LSB replacement methods,” IEEE Proceedings on Vision, Image and Signal Processing, Vol. 152, No. 5, pp. 611-615, (2005)
8. C.-M. Wang ,A high quality steganographic method with pixel-value differencing and modulus function.,The Journal of Systems and Software (2007)
9. M.U. Celik, G. Sharma, A.M. Tekalp, E. Saber, Lossless generalized- LSB data embedding, IEEE Trans. Image Process. 14 (2) 253–266 (2005).
10. C.C. Chang, T.C. Lu, A difference expansion oriented data hiding scheme for restoring the original host images, J. Syst. Software 79 (12) 1754– 1766,(2006)
11. Z. Ni, Y.Q. Shi, N. Ansari, W. Su, Reversible data hiding, IEEE Trans. Circuits Syst. Video Technol. 16 (3) 354–362 (2006).
12. Ching-Chiuan Lin∗, Nien-Lin Hsueh ,Alossless data hiding scheme based on three-pixel block differences , Pattern Recognition 41 1415 – 1425,(2008)
13. Chih-Chiang Leea, Hsien-ChuWub, Chwei-Shyong Tsaic,Yen-Ping Chud, Adaptive lossless steganographic scheme with centralized difference expansion, Pattern Recognition (41) 2097– 2106,(2008)
14. J. K. Mandal and Debashis Das, Steganography Using Adaptive Pixel Value Differencing(APVD) of Gray Images Through Exclusion of Overflow/Underflow, CS & IT-CSCP (2012)