The emergence of artificial neural networks in signal processing has led to improvements in signal compression. In this paper a comparison of ECG signal compression using Multi Layer Perceptron(MLP) neural network and Particle Swarm Optimisation(PSO) is made. For this different back propagation artificial networks are used as compressor and decompressor. Particle swarm optimisation (PSO) is used for optimising the learning rate and momentum. The proposed algorithm yields minimum mean square error for the ECG signals from MIT-BIH arrhythmia data base.
Keywords |
| Compression, Mean square error, Multi Layer Perceptron neural network, Particle Swarm Optimisation |
INTRODUCTION |
| Of the various Bio signals, ECG signals are important in modern clinical systems that require the storage,
processing and transmission of large quantities. The goal of compressing and transmitting data over the network is to
make the data to be sent as small as possible. Moreover, apart from decreasing the size of the original data, as much of
the original information as possible must be retained when dealing with medical information. Since it is required to
record a signal during 24 hours, the computer storage may arise up to several Giga Bytes. Considering the several
million medical signals annually recorded for the purposes of comparison and analysis, the need for effective data
compression techniques is becoming increasingly important. Many algorithms for ECG compression have been
proposed in the last thirty years. Artificial Neural Networks are systems which make use of some organizational
principles resembling those of human brain. In this paper section I gives the introduction. Section II deals with multi
layer perceptron neural network and its direct application to signal compression. Section III deals with the principle of
particle swarm optimisation. In section IV results and its analysis are dealt with and finally section V concludes the
work followed by references. |
MULTI LAYER NEURAL NETWORKS FOR ECG SIGNAL COMPRESSION |
| Multi layer neural networks with back propagation algorithm can directly be applied to signal compression. |
| A. BACK PROPAGATION LEARNING ALGORITHM |
| Based on this algorithm, the networks learn a distributed associative map between the input and output layers.
In this the weights are calculated during the learning phase of the network and in this respect this algorithm differs from
the others. In general, difficulty with multilayer perceptions is in calculating the weights of the hidden layers in an
efficient manner that results in the least (or zero) output error; the more hidden layers there are; the more difficult it
becomes. To update the weights, one should calculate an error. At the output layer this error is easily measured; this is
the difference between the actual and desired (target) outputs. At the hidden layers however, there is no direct
observation of the error, hence some other technique must be applied to calculate error, as this is the ultimate goal. |
| B. LEARNING WITH BACK PROPAGATION ALGORITHM |
| During the training session of the network, a pair of patterns is presented (xk ,dk), where xk is the
input pattern and dk is the target or desired pattern. The xk pattern causes output responses at each neuron in
each layer and hence actual output y
k at the output layer. At the output layer, the difference between the
actual and target outputs yields an error signal. This error signal depends on the values of the weights of the
neurons in each layer. This error is minimized, and during this process new values for the weights are
obtained. The speed and accuracy of the learning process (i.e).the process of updating the weights also
depends on factor known as the learning rate. |
| The basis for this weight update algorithm is simply the gradient method as used for simple
perceptrons with differentiable units. For a given input – output pair (xk’, dk’) the back – propagation
algorithm performs two phases of data flow. First, the input pattern ax’ is propagated from the input layer to
the output layer and, as a result of this forward flow of data, an actual output yk is produced. Then the error
signals resulting from the difference between dk and yk are back - propagated from the output layer to the
previous layers for them to update their weights. |
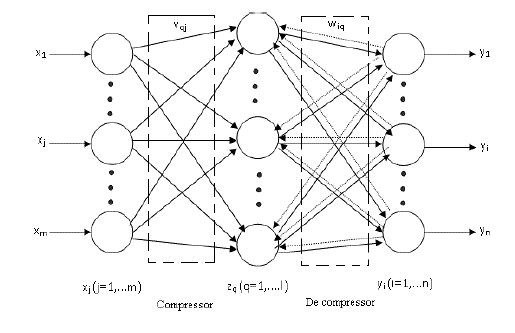
| Let us consider 'm' PEs (Processing Elements) in the input layer, 'l' PEs in the hidden layer and „n‟
PEs in the output layer as shown in Fig 1. |
| Consider an input – output training pair (x, d) a PE q in the hidden layer receives a net input of |
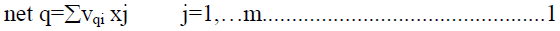 |
| And produces an output of |
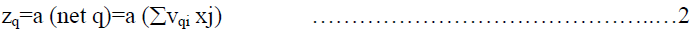 |
| The net input for a PE 'i' in the output layer is then |
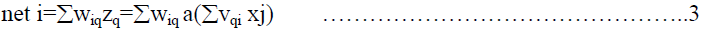 |
| and it produces an output of.. |
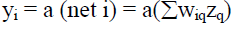 |
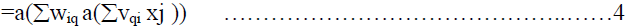 |
| The above equations indicate the forward propagation of input signals through the layers of neurons.
Next, we shall consider the error signals and their back propagation. |
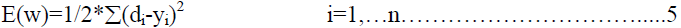 |
| Then according to the gradient method the weights in the hidden to output connections are updated
by |
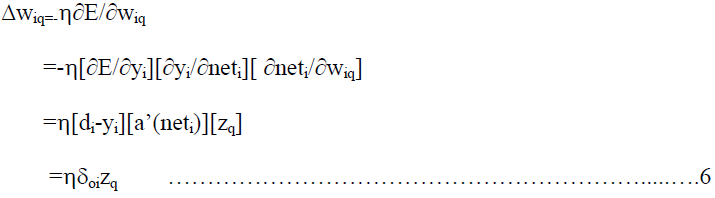 |
| where δoi is the error signal and its double subscript indicates the 'i'th node in the output layer. The
error signal is defined by |
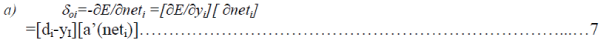 |
| For the weight update on the input to hidden connect ions, the chain rule wi th the
gradient method i s appl ied and the weight update on the l ink weight connect ing PE j in the
input layer to PE q in the hidden layer i s obtained. |
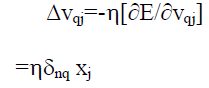 |
| where δnq is the error signal of PE q in the hidden layer and is defined as |
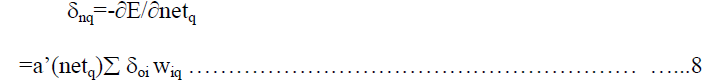 |
| where netq is the net input to the hidden PE q. The error signal of PE in a hidden layer is different
from the error signal of a PE in the output layer. Due of this difference, the above weight update procedure
is called the generalized delta-learning rule. |
| The process of computing the gradient and adjusting the weights is repeated until a minimum error
is found[6]. In practice, one develops an algorithm termination criterion so that the algorithm does not
continue this iterative process forever. |
| The back – propagation algorithm can be outlined as |
| Step 1 : Initialize all weights to small random values. |
| Step 2 : Choose an input-output training pair. |
| Step 3 : Calculate the actual output from each neuron in a layer by propagating the signal forward through
the network layer by layer (forward propagation). |
| Step 4 : Compute the error value and error signals for output layer. |
| Step 5 : Propagate the errors backward to update the weights and compute the error signals for the preceding
layers. |
| Step 6 : Check whether the whole set of training data has been cycled once, if yes go to step 7; otherwise go
to step 2. |
| Step 7 : Check whether the current total error is acceptable; if yes, terminate the training process and output
the field weights, otherwise initiate a new training epoch by going to step 2. |
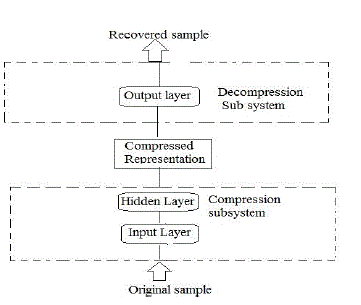
| The back-propagation algorithm is one of the most popular methods to train the artificial neural
network[2]. The architecture of the compression scheme is shown in Fig 2. |
PARTICLE SWARM OPTIMIZED NEURAL NETWORK (PSONN) |
| Particle Swarm Optimisation (PSO) is a population based stochastic optimization technique. The
potential solutions called particles fly through the problem space and this is achieved by following the current optimum particles. The merits of PSO are that it is easy to implement and a few parameters to be
adjusted. The algorithm is initialized with a group of random particles (solutions).Searches for optima by
updating generations is done. Two best values are followed for updating each particle in every iteration. The
best solution that has been achieved so far [fitness] is denoted as pbest. This fitness value is the mean square
error and is also stored. The best value (tracked by the particle swarm optimizer) obtained so far by any
particle in the population is called gbest. Best value becomes local best (called as lbest) when a particle takes
part of the population as its topological neighbors. After finding the two best values, the velocity and
positions of the particle is updated with the following equations. |
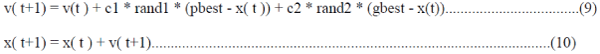 |
| Where, v(t ) is the particle velocity, x(t ) is the current particle (solution), and rand1 and rand2are random
numbers between (0,1). c1, c2 are learning or acceleration constants.
The pseudo code of the procedure is as follows |
| Randomly generate initial population |
| Do |
| For each particle |
| Fitness value ( Mean square Error ) is calculated. |
| If the fitness value is better than the best fitness value (pBest) in history |
| set current value as the new pBest. |
| End |
| Choose the particle with the best fitness value of all the particles as the gBest |
| For each particle |
| Particle velocity is calculated according to equation(9) |
| Particle position is updated according to equation (10) |
| End |
| while maximum iterations is reached. |
| No guarantee of converging to the global optimum with the back propagation is noticed when the
configuration is made to train a number of times. But However a better performance configuration can be
achieved in the architecture defined by the optimality of the network evolved using PSONN. In the proposed
method, PSONN is applied for evolving fully connected feed forward Neural Network and is optimized with
best network architecture by optimizing the learning rate and the momentum factor.During the presentation
of unusual pair of training patterns, major disruption of the direction of learning is avoided by finding an
optimal learning rate. The advantage of using optimal momentum factor is to accelerate the convergence of
error propagation algorithm. Two range arrays define the range of the optimization process. They are Rmin =
{ Lrmin, Mcmin} and R max ={ Lrmax, Mcmax }where, Lr is the learning rate and Mc is the momentum factor.
tansig is the activation function used. |
| The fitness function for optimal training is the Mean Square Error (MSE) and is given by, |
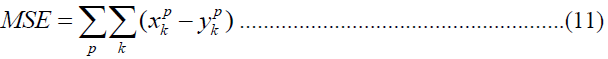 |
| Where x is the target (desired) output, and y is the actual output from the kth neuron in the output layer for
the pattern p in the training set. With the framed fitness function, the PSONN algorithm automatically
evolve a best solution. |
RESULTS AND ANALYSIS |
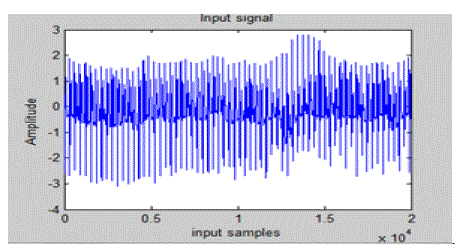
| Testing of 48 ECG signals of MIT – BIH arrhythmia database[1] with the proposed algorithm was
done using MATLAB. 20000 samples are taken and the compression ratio is 80. Input signal 107 is shown
in Fig.3 In this section the optimality of the network configuration with respect to the MSE criterion is
evolved automatically by PSONN algorithm |
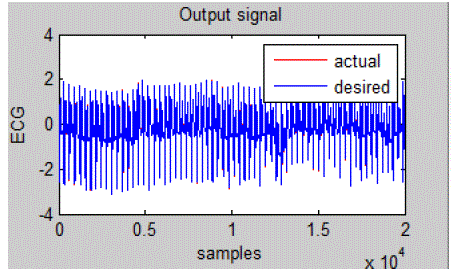
| Reconstructed signal with feed forward network for the signal 107 is shown in Fig.4. And the
reconstructed signal with feed forward network and Particle Swarm Optimised neural network for the signal
107 is shown in Fig.5. The mean square error obtained by the compression using back propagation
algorithm is too small compared to the error obtained by direct and transform methods of signal
compression[4],[5],[10] and [11]. The time taken by scaled conjugate gradient algorithm is less compared to
Levenberg -Marquardt algorithm for computation.. Particle swarm optimisation (PSO) is used for optimising
the learning rate and momentum factor. The proposed algorithm yields minimum mean square error for the
ECG signals from MIT-BIH arrhythmia data base. Comparison of typical ECG signals of MIT- BIH
database is given in TABLE I. |
CONCLUSION |
| The mean square error obtained by the compression using artificial neural network is too small
compared to the error obtained by direct and transform methods of signal compression. Particle swarm
optimised neural network further reduces the mean square error. The results demonstrate that the optimized
feed forward Neural Network has yielded best performance when compared to back propagation algorithms.
Hence particle swarm optimised artificial neural network is an improved compression scheme for ECG
signals. |
ACKNOWLEDGEMENTS |
| The authors would like to thank Research Centre, LBS Centre for Science and technology for
providing facilities to carry out this work. |
| |
Tables at a glance |
 |
| Table 1 |
|
| |
Figures at a glance |
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
|
| |
References |
- http://www.physionet.org / physiobank
- JiZhenyan, Deng Shanxi, A Compression System of ECG Data Based on Neural Networks, proceedings of ICSP‟98
- Khalid, Sayood, Introduction to data compression, 3rd edition, Elsevier India.
- M.J.Jayashree ,Prof. (Dr.) A. Sukesh Kumar, Resourceful scheme of ECG compression using different Wavelet transforms and PDLZW, 2011 3rd International Conference on Electronics Computer Technology (ICECT 2011) , Kanyakumari, India , April 2011.
- M. J. Jayashree Prof. (Dr.) A. Sukesh Kumar, Effectual compression of ECG using different Wavelet transforms,Vectorquantisation and PDLZW method, International Conference on Intelligent System and Data Processing (ICISD 2011), G H Patel College of Engineering andTechnology, VallabhVidyanagar, January 2011.
- Narayanan Sreekumar, Dr. S.SanthoshBaboo, Neural Network based Complex Image Compression using Modified Levenberg-Marquardt method for Learning.I S S N: 2 2 2 9 - 4 3 3 3( P r i n t ) | I S S N : 0 9 7 6 - 8 4 9 1 (On li n e)
- Rajesh Kumar, Fundamentals of Artificial neural network and Fuzzy logic, University Science Press,154.2009.
- Vilas H. Gaidhane1, Vijander Singh1, Yogesh V. Hote2, Mahendra Kumar, New Approaches for Image Compression Using Neural Network,Journal of Intelligent Learning Systems and Applications, Published Online November 2011 (http://www.SciRP.org/journal/jilsa) Copyright © 2011 SciRes. JILSA, Vol 3, pp : 220-229,2011.
- YucelKogyigitr, Mehmet Kororekr, BekirKarlikz , ECG data compression using artificial neural networks ''ELECO'99 , International conference on Electrical and electronics engineering.
- A. Rios and M. Kabuka,"Image compression with a Dynamic Autoaasociative Neural network", Mathl. Comput. Modelling Vol. 21, No. l/2, pp. 159-171, 1995.
- M. J. Jayashree, Prof. (Dr.) A. SukeshKumar,”Comparison of Neural Network Based ECG Signal Compression using Feed- Forward and cascade correlation Back Propagation networks” International Journal of Mobile and Adhoc Network,Vol2,issue 1,pp : 34-38, Feb 2012.
- M. J. Jayashree Prof. (Dr.) A. Sukesh Kumar, “Compression of ECG after baseline removal using Wavelet transform , Vector quantisation and PDLZW encoding”National conference on Emerging Technologies- 2012,Govt. Engineering College, Barton Hill, Thiruvananthapuram, Kerala,India, July 2012.
|