International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

An Intelligent Technique for Generating Equivalent TT Circuits Using Genetic Algorithm

Nariman A. Khalil1, Rania F. Ahmed1, Rania. A. Abul Seoud1, Ahmed M. Soliman2
  1. Electrical Department, Faculty of Engineering, Fayoum University, Fayoum, Egypt
  2. Electronics and Communication Engineering Department Cairo University, Cairo, Egypt
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The TT filter is a basic building block in many analog signal processing applications. Genetic algorithm applications in analog design circuits play an important role with promising results. This paper introduces the TT_GA Technique. It is an intelligent technique for generating equivalent TT Circuits using genetic algorithm realization with Nullor and Pathological elements. The goal is to generate equivalent Second Generation Current Conveyor (CCII) as well as equivalent Transconductance Amplifier (TA) circuits. This Technique generates 8 different TT circuits using CCII circuits. Also, it generates 16 circuits using TA. Some of thegenerated TTcircuits and the conventional op-amp realized filtersare simulated using SPICEand compared to each other’s.A standard CMOS model of 0.25 μm is used.By applying the TT_GA Technique we can get all possible solutions programmatically.

Keywords
TT filter, Genetic algorithm, nullor representation, CCII circuits, TA circuits.

INTRODUCTION
The symbolic analysis is a powerful tool to analyse electronic circuits, where all parts of the circuit elements are considered symbols. The nullor is quite useful for the analysis, synthesis, and design procedures, as it facilitates modelling the behaviour of any active device disregarding the particular realization of the active blocks [1]-[6]. It is well known that the nullator norator combinations cannot realize the CCII+, ICCII+ and ICCII− unless additional resistors are used as demonstrated in [1], [2].The pathological voltage mirror (VM) and the pathological current mirror (CM) introduced in [3] and [4] provided means of representing the four single-output CCII and ICCII members without any need to use resistors [3]. The systematic synthesis of active circuits developed in [5], [6] is based on using the nullor elements, the basic ideas were extended in [7], [8] to accommodate the pathological mirror elements allowing more ideal representations of active circuits.
The Genetic Algorithm (GA) is such an optimization technique which operates on the principle of "survival of the fittest". GA has the capability to generate new design solutions from a population of existing solutions, and discarding the solutions which have an inferior performance or fitness [11]. TheGA starts from high-level descriptions to automatically synthesize analog circuits. However, automatic synthesis of analog circuits from high-level specifications is recognized yet as a challenging problem [9]-[12].It is worth noting that the genetic algorithm with nullator-based descriptions was applied to generate Voltage Followers (VFs) circuits and in [11]. This method described how an automatic system can deal with huge search spaces to design practical VFs by performing evolutionary operations from nullator-based descriptions.Also, generation of Voltage Mirrors circuits (VMs) based on genetic algorithm was presented in [12]. Moreover, [9]introduced a new genetic algorithm to synthesis the negative type CCII- blocks by superimposing VFs and current followers (CF).
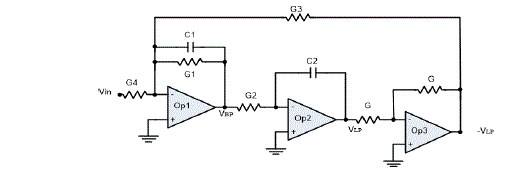
The Tow-Thomas (TT) second order filter using operational amplifiers (op-amps) has been reviewed in [15]. Passive and active compensation methods to improve the circuit performance for high designs were also reviewed. It is well known that the classical TT circuit using op-amps has frequency limitations due to the finite gain-bandwidth of the opamps. The Tow-Thomas biquad of fig.1 is an active-RC topology used to realize both lowpass and bandpass biquadratic filtering. This topology has been widely used because it is simple, versatile, ad require few components.
This paper introduces a new methodology based on nullor and pathological elements to generate equivalent CCII and TA – TT circuits. Another method to obtain equivalent TT circuits, based on NAM expansion, was proposed in [15]. But the advantage of the proposed GA methodology is that it can generate all possible circuits programmatically and also, it can be applied to any op-amp circuit other than TT to get CCII or TA equivalent circuits.
The paper is organized as follows; the proposed methodology is described in section II. In section III, the methodology is applied to TT circuit to get CCII-TT equivalent circuits. TT_GA is also applied to get TA-TT equivalent circuits in section IV. Finally, section V concludes the work.

METHEDOLOGY
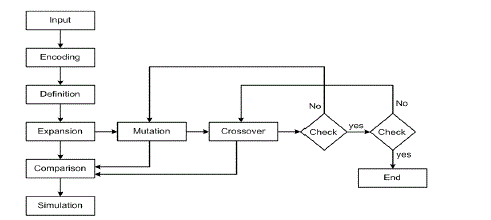
The proposed algorithm of the GA is carried out in steps as shown in fig. 2. Firstly, the nodal equation for the circuit is to be written in the form [Y][V]=0, so that element count can be extracted. The number of nonzero elements in the Y matrix represent the total number of elements of the circuit, a single increment of the number of rows represent the number of original nodes, the number of diagonal elements represent the number of grounded elements, and the reminder elements are thus the floating ones.Secondly, all the passive elements are to be encoded in genes, and the floating passive elements are to be expanded as follows: Each element is represented by a gene of the formGen:R∙C∙S, where R is the row number, C is the column number, and S is a sign bit. The sign bit is 1 for positive elements while it is equal to 0 for negative elements. Considering that if the column and row numbers are equal, so the element is grounded and it is represented for simplicity by Gen:R∙0 otherwise an expansion subroutine for the element is applied. Table I shows the encoding of the Nullor and the pathological elements.
The current conveyors types considered in this work are CCII+, CCII-, ICCII+, and ICCII- which are presented in [7], [8], [16]. These current conveyors can be codified in genes and it can be represented as shown in Table II. Recently a systematic generation method of TA based on nullor elements and pathological mirror elements was employed to provide pathological realizations of different types of TA [17], [18]. The Balanced Output TA (BO-TA) and the Single Output TA (SO-TA) are the two different types of the TAs. In this work, only Single-input-Single- Output SISO-TA will be considered.There are four configurations for SISO-TA. To facilitate dealing with them in the proposed algorithm, each one can be codified in genes and represented in the Nullor form as shown in Table III. The gene codification of positive resistances can be obtained using the first and the second configurations while negative resistances can be obtained using the third and fourth configurations.
Third, a subroutine for the floating elements is to be applied. The elements are expanded based on the sign bit (S). If S is 1; which means that it is positive element, thus the gene is written as: Gen/passive element = R.N.P.N.C.O.OR Gen/passive element -R.N.I.N.C.V. where N is the insertion node. On the other hand, if S is 0; which means that it is negative element, so, the gene is written as: Gen/passive element R.N.I.N.C.O.OR Gen/passive element R.N.P.N.C.V The generated genes of the passive elements are then compared to that of the active counterpart whose equivalent circuits are given in Tables II and III. The generated circuit is then tested for the optimum ωO AND Q The genes then are arranged together to form a chromosome. A mutation operation (bit inversion) is then applied to each gene in the chromosome. The genes resulted from the subroutine described before. The mutated genes and the genes of the active elements are also compared. The performance of the generated circuits are also tested for optimum ωO AND Q
Further circuits can also be generated by crossing over the genes which have the same sign. Mutation and crossover is carried out for the rest of the genes. The total number of generated circuits from that procedure is 2 no. floating elements.

GENERATING CCII EQUIVALENT CIRCUITS USING TT-GA
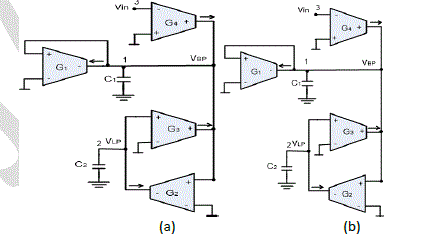
The nodal equations for the op-amp TT circuit shown in fig. 1can be written as follows:
(sC1+G1 VBP − G3VLP + G4 VIN = 0 (1)
G2VBP + sC2VLP = 0 (2)
The transfer functions of the two output responses (bandpass and lowpass responses) are given by:
image (3)
image(4)
The centre frequency and the quality factor are as follows: image
A. analysis:
The proposed methodology is applied to the TT circuit configuration as follows:
Step 1: The nodal equations of this circuit can be written as follows:
image (5)
Step 2: Extract the No. of elements which is equal to 5.
image
image
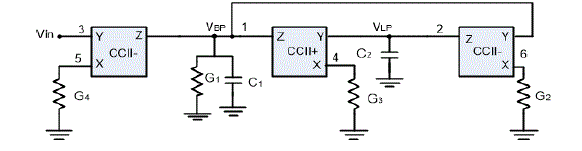
Comparing between genes of CCII family representations and the resulted chromosome, we can find that Gen4 can be represented by CCII- , Gen2 is represented by CCII+ and Gen3 is represented by ICCII+.The final realization is shown in fig. 4(a).
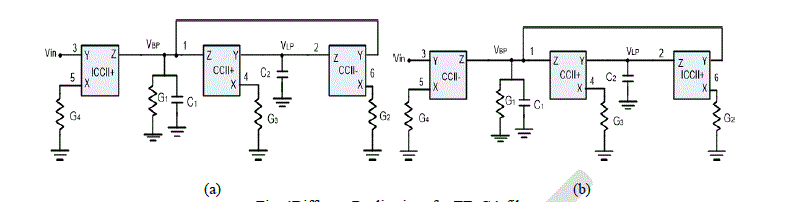
Also, if a crossover operation is applied between genes Gen|G4 . Gen|G2 (just crossover between active elements), one can get the following new chromosome:
Chromosome expanded elements= 1.4.I.4.2.O.1.5.P.5.3.O.2.6.I.6.1.V
Comparing between genes of CCII family representations and the resulted chromosome, we can find that Gen3 can be represented by CCII- , Gen2 is represented by CCII+ and Gen4 is represented by ICCII+. The final realization is shown in fig. 4(b).All possible realizations are summarized in Table IV. It is worth noting that these realizations are the same obtained in [2].
B. Simulation results:
It may be of interest to show simulations of some of the generated CCII equivalent TT_GA circuits. For a fair comparison among the different circuits, the same CMOS generalized conveyor circuit presented in [19], [20] is used in the simulations. The supply voltages used are±1.5V. The equivalent CCII TT_GA circuits of fig. 3 and 4 are designed for Q= 10 and f0=1MHztakingC1=C2=5 pF, R= R2=R3=15.9 kΩ, R4= 10kΩ and R1 = 159 kΩ. 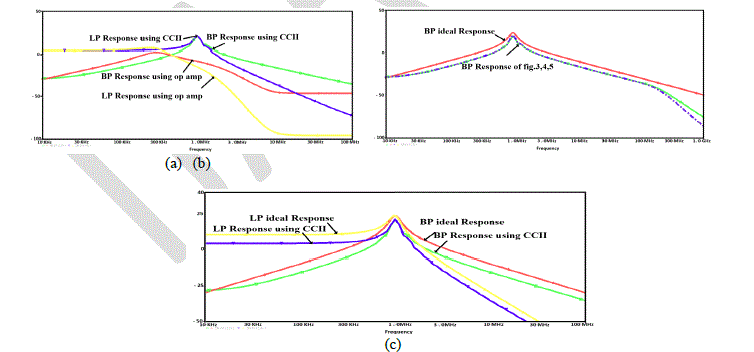The input signal is a sinusoidal input voltage source of 1 V magnitude. Fig. 5(a) represents Magnitude responses comparison between the CCII-TT configuration of fig. 3 and the op-amp TT realization of fig.1. As shown in this figure, the op-amp is malfunction at frequencies [17] but CCII can operate in high frequencies with lowest error so it is very useful to realize TT using CCII.
The comparison among the BP magnitude responses ofCCII- TT differentrealizations of figs. 3and 4 and the ideal response is shown in fig. 5(b). This figure proves that the three configurations have the same response. Fig. 5 (c) shows the magnitude response of CCII- TT_GA filter of fig. 4(a) compared to the ideal response with error less than7.5% in the centre frequency and 10% for the quality.

GENERATING TA-TT EQUIVALENT CIRCUITS USING TT_GA
A:Analysis:
In this section, the proposed algorithm is applied to get the TA-TT equivalent circuits. Steps 1, 2 and 3 are the same as in the previous section. Note that the grounded resistance is realized using TA as shown in fig. 6. Here, the realization of fig. 6 (a) is used to represent the grounded transconductance G1.
Step 4: The Chromosome represents the expanded elements is as follows:
Chromosome expanded elements= Gen2|−G3 . Gen3|G4 . Gen4|G2 .
If we use the first possible to all genes the chromosome will be:
Chromosome expanded elements= 1.4.I.4.2.O.1.5.P.5.3.O.2.6.P.6.1.O
Comparing between genes of SO-TA family representations and the resulted chromosome, one can find that Gen2 can be represented by the TAI+ in table III with negative terminal is grounded, positive terminal is connected to node 2 and output terminal is connected to node 1. Where, Gen3 andGen4 are represented by the TAI- 1in table III. +. The final output file is as follows:
sC2 2 0 sC1 1 0 G1 1 1 TAI+ 1 2 TAI- 1 3 TAI- 2 1
Note that the output responses; VBP and VLP are taken from nodes 1 and 2 respectively and the input is injected through node 3. The final realization is shown in fig. 7(a).
As there are three floating elements and grounded element which is also represented by TA and every element has two configurationsand each configuration can be represented by two genes, so, 44= 256 different forms of the equivalent nullor–mirror realizations for the filter and 24= 16 equivalent SO-TA- realizations are available. Those realizations are achieved by applying mutation and crossover between genes.For example, applying mutation operation to the second gene results in the following new chromosome:
Chromosome expanded elements= 1.4.I.4.2.O.1.5.I.5.3.V.2.6.P.6.1.O
After mutation the nullor representation of the circuit change and Gen3 can be represented by the TAI- and TAO- in table III as we use TAI- in the first realization so we will use TAO-. Gen4 is represented by the TAI-and Gen2 can be represented by the TAI+. The final realization of TT_GAwith SO-TA is shown in fig. 7(b). All possible solutions of the circuit are summarized in table V.
B. Simulation Results
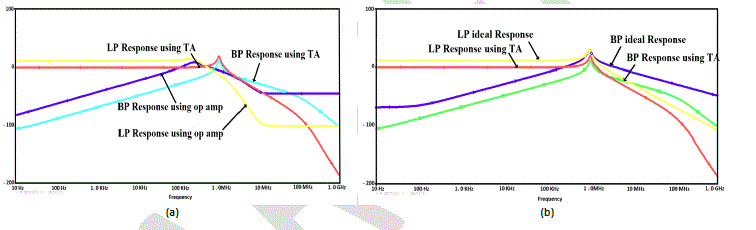
P-Spice simulations were carried out to verify the performance of the equivalent TA-TT_GA circuits. The CMOS realization of the TA circuit used for simulation is given in [21] with 0.25μ model and supply voltages of ±1.5V. The TA-TT_GA circuit of fig. 7(a)is designed to have f0=1MHz and Q = 10. The input signal is a sinusoidal input voltage source of 1V magnitude. Fig. 8(a) shows the BP and LP magnitude responses of TA-TT_GA configuration of Fig. 7(a) compared with the original op amp TT circuit. It is clear that the TA circuit has a superior performance than the original TT one. A magnitude response comparison between TA-TT_GA configuration of Fig. 7(a) and the ideal response is shown in fig. 8(b). This figure shows that the errors in the centre frequency and the quality factor are less than 10% and 5% respectively.

CONCLUSIONS
The paper presented a family of TT_GA equivalent circuits. First a new generation methodology, based on the nullor representation and the GA, was introduced. This methodology was applied on the TT circuit, instead of the NAM expansion method, to generate 8 CCII-TT equivalent circuits. It was also applied to generate 16 SO-TA-TT equivalent circuits. it was the first time that uses GA to realize CCII-TT and SO-TA-TT which help us to get all possible circuits programmatically. The generated circuits have been confirmed using PSPICE simulation and the simulation results showed that some generated circuits have better performance compared with the original TT configuration. It is worth noting that the proposed methodology represents a systematic generation method and can be applied to any other op amp circuit to generate equivalent CCII or TA ones.

Tables at a glance


Table icon Table icon Table icon
Table 1 Table 2 Table 3
Table icon Table icon
Table 4 Table 5
 

Figures at a glance


Figure Figure Figure Figure
Figure 1 Figure 2 Figure 3 Figure 4
Figure Figure Figure Figure
Figure 5 Figure 6 Figure 7 Figure 8
 

References