Keywords
|
| SHID, HASH, Poly Pool, SBIDB, TRADE-KP, WSN |
INTRODUCTION
|
| Wireless Sensor Networks are used in many real time applications such as environment monitoring, health monitoring, military applications, industrial monitoring, etc. Sensors are small in size, and have wireless communication range capability within short distances. A distinctive sensor node contains a sensing unit, power unit, a storage unit, a wireless transceiver and a processing unit. A WSN composed of large figure of sensor nodes with communication capabilities, computation, storage and limited power. Environments, where sensor nodes deployed are controlled such as home, office, warehouse, forest, etc. and uncontrolled such as hostile areas, disaster areas, toxic regions, etc. However, manual deployments become infeasible and even impossible as the number of the nodes increases. At a certain spots it is possible to provide denser sensors, but it may not be possible to control all the nodes. Thus, earlier the network topology cannot be defined exactly. Though the information of topology can be obtained by the way of sensor nodes and self-deployment protocols, for large scale wireless sensor network this may not be possible. |
| Six Security challenges in WSN are: (i) nature of Wireless communication, (ii) limitation of resource on sensor nodes, (iii) very dense and large WSN, (iv)lack of infrastructure fixed, (v) prior to deployment network topology is unknown, (vi) to unattended sensors high risk of physical attacks. In certain cases sensor nodes are require to operate under harmful condition. Security of such conditions is based on the efficient key pre-distribution scheme. To visit large amount of sensor nodes, and change their configuration in uncontrolled environments it is infeasible, or even impossible. In addition, using single shared key for the whole network may lead to obtain the key from the advisor. Thus, to establish the secure network, the sensor network must adopt the environment by using the pre-distributed keys, inorder to exchange the information with their immediate neighbors. In WSN Key distribution and management problem difficult one, and the new approaches are required. Motivation of this paper is to design the efficient key predistribution scheme and to compare it with the existing algorithms to prove that it is efficient than other schemes. This paper deals with related work in section II. The comparative study of various existing and proposed scheme with its performance analysis is made in section III. Finally it is concluded in section IV. |
RELATED WORKS
|
| The problems in Key management WSNs have been extensively studied in the literature and the key predistribution solutions have been compared with the proposed SHI-KPD’s scheme. |
| Eschenauer and Gligor [1] proposed a random key pre-distribution scheme called RKP. In this scheme each node is pre loaded randomly with k keys from S pool. This scheme yields a high connectivity and not resilient against node capture since the capture of one node can compromise the whole network. |
| Chan et al. proposed in [2] a protocol called Q-composite scheme that enhances the resilience of RKP. Two nodes can establish a secure link only if they share at least Q keys. The pairwise session key is calculated as the hash function of: Ki,j = Hash(Ks1||Ks2||…..||Ksq’) where Ks1, Ks2, ...Ksq’ are the q’ shared keys between the two nodes i and j (q’≥ Q). This approach enhances the resilience against node capture attacks because the attacker needs more overlap keys to break a secure link. |
| Blom [3] proposed a λ-secure symmetric key generation system in which uses two matrices public G matrix and private A matrix, where G matrix are known to all adversaries and for each node a unique row from the private matrix A=(G.S) is allotted, where G,S be the public vandermone and secret symmetric matrix respectively. The pairwise keys are generated by Ki,j=G.AT |
| Ruj et al. [5] proposed a Trade Based Key Management Scheme which consists a finite set X of v elements, a Steiner trade t − (v, k) is defined to be two disjoint groups T1and T2 of k-elements blocks of X such that each set of t elements from X occurs in exactly the same number of blocks of T1 as of T2. After deployment each node can establish a direct link if they share exactly two common keys which can be used for computing pairwise session key. And have proved that each pair of keys occur exactly two nodes in T1 and T2 respectively or no nodes. |
| Du et al. [6] proposed a scheme called enhanced random scheme assuming node before deployment knowledge. Every nodes are assigned with key from the regional key pools. The key pools are formed in a way that neighbouring keys from the corresponding key pool. |
| Camtepe and Yener [7] proposed key pre-distribution scheme named as Symmetric Balanced Incomplete Block Design (SBIBD). The proposed mapping from this scheme to key pre-distribution has to construct m2+ m+1 key rings from a key pool S of m2+ m +1 keys. The pairwise keys are generated by each contain k=m+1 keys. |
COMPARATIVE STUDY
|
| The key distribution scheme is used for the communication between the sensor nodes for the passing of information from the sensor node to the end user through wireless communication without interrupt from the external elements such node failure, from snoopers and more. So for preventing from the snoopers from the active and passive attacks we are going for an key distribution scheme by which the nodes can be prevented by generating keys for the key predistribution scheme. Thus the generated keys should not be captured by the attackers for solving these problems we propose a novel key pre-distribution scheme called SHID-KPD scheme for improving the resilience. |
A. HASH FUNCTION ALGORITHM
|
| In this scheme a part of original keys will be converted into derivate keys and they are assigned to every sensor before sensor nodes deployment. After the pairwise keys establishment between sensor nodes the original keys in every sensor nodes are then converted into derivative keys. Then all original keys will be then erased from the sensor memory. Because it is computational impossible to revert the Hash function, attackers can’t get other sensor nodes information from any compromised sensor nodes. |
| Let the number of total captured sensor nodes be x. Hence, we have the probability Pb, that any secure link between two uncompromised sensor nodes is compromised when x sensor nodes have been captured is |
 |
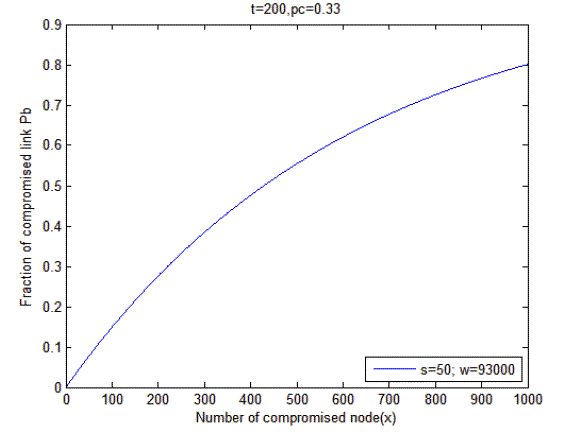
| Where t is the number of keys assigned to sensor nodes, s is the number of derivative keys in every sensor Figure 1 shows the resiliency of the HASH Function algorithm during pairwise key establishing. The performance analysis of hash function is shown in figure 1. It is observed that if 500 nodes get compromised then Pb is 0.5.From this we understand that the resilience become stronger when the number of derivative key increase. |
| B. POLYNOMIAL POOL-BASED KEY PREDISTRIBUTION SCHEME |
| In polynomial pool-based key pre-distribution scheme the key setup server randomly generates bivariate t-degree polynomials with coefficients over a finite field GF(λ), where λ is a prime number large adequate to accommodate a cryptographic key. |
| A pool of |S| random bivariate polynomials, each with a unique id, namely, degree t, and a pool of |Sk| random generation keys each with a unique identification. Prior to network deployment, for every sensor node u, the setup server randomly picks a subset of s polynomials out of |Sp| and assigns polynomial shares of these s polynomials to the sensor node. In addition, for every sensor node u, the setup server randomly selects a subset of k(k<s) generation keys out of |Sk| and assigns them to the sensor node u. |
| The poly pool-based key pre-distribution scheme uses the below equation for calculating the probability of resilience against the number of compromised node |
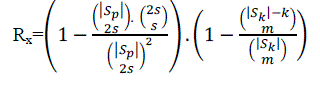 |
| C. Symmetric BIBD |
| SBIBD is called Symmetric BIBD or Symmetric Design. The SBIBD has four properties: |
| 1) Each block contains k=r objects |
| 2) Every object occurs in r=k blocks |
| 3) Every pair of objects occurs in λ block |
| 4) Every pair of blocks intersects on λ objects. |
| The SBIBD scheme of order m, the network resiliency when x nodes are captured is |
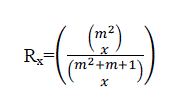 |
| D. Unital Design for Key Pre-Distribution in WSN |
| A Unital design is a Steiner t-design which consists of b = m2(m2−m+1) blocks, of a set of v = m3+ 1 points. Each block contains m + 1 points and each point is contained in r = m2 blocks. Each pair of points is contained in exactly one block together. We denote the Unital by t-design(m3+ 1, m2(m2− m + 1), m2, m + 1, 1) or by (m3+ 1, m + 1, 1)design for simplicity sake. |
| Unital scheme of order m, the network resiliency when x nodes are captured is |
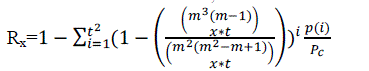 |
| Let p(i) is the probability that two nodes share exactly i keys and that Pc is the probability that two nodes share at least one key. |
| Where |
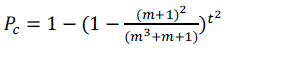 |
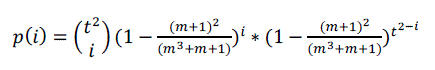 |
| E. Trade-KP. |
| The trade-based key management scheme denoted Trade-KP. Given a finite set X of v elements, a Steiner trade t − (v, k) is defined to be two disjoint sets T1and T2 respectively. The k-elements blocks of X and t elements from X occurs in precisely the same number of blocks of T1 as those of T2. This t elements from X is not repeated more than once in any of T1 or T2. The proposed scheme uses trade construction having q as prime power and k lies between (4 ≤ k < q). The constructed T1 and T2 blocks are represented by t 1 i,j= {(x, (xi + j ) mod q) : 0 ≤ x < k}, where 0≤ i, j < q , and T2 represented by t2 i,j= {(x, (x2+ xi + j ) mod q): 0 ≤ x < k}, where 0 ≤ i, j < q . Authors proved that the proposed construction results in a 2 − (qk, k) strong steiner trade. They proposed then a mapping to key pre-distribution where they associate to each element a distinct key and to each block of T1 and T2 a key ring. The key ring size is then equal to k and the scalability of the scheme is equal to 2q2 . |
| The TRADE scheme uses the below equation for calculating the probability of resilience against the number of compromised node |
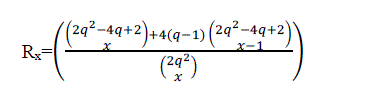 |
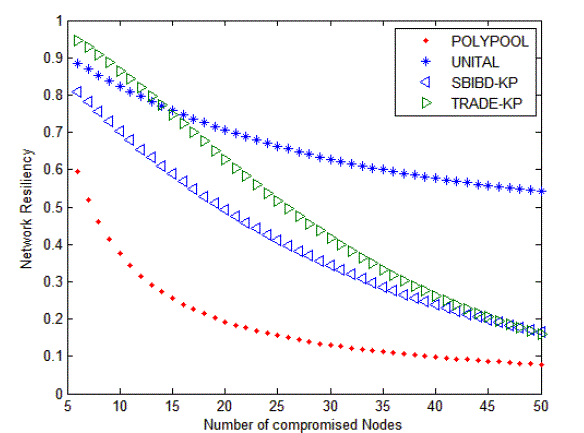
| Figure 2 explains the resiliency of the network against the number of compromised node for different key predistribution scheme such as POLYPOOL, UNITAL, SBIDB, TRADE scheme. Thus from this unital provides a better results while comparing to other schemes. |
| F. SHI-KPD Scheme (Proposed Scheme) |
| By using Symmetric, Hankel and Identity matrices for making the Pre-distribution scheme more secure between the sensor nodes by fasten methods we propose a fangled Pre-distribution scheme and named it as SHI-KPD scheme. Earlier the D (key space) is calculated using the product of S (private-symmetric) and I (vandermonde matrix-Public) but the proposed scheme uses square of Symmetric(private), Hankel (public) and Identity matrices on some mathematical combinations which is shown in equation (1) below inorder to make the computational more complex to improve security in generating key which is to be assigned in each sensor node for formation of secure link. |
 |
| In general matrix K can be represented as shown below and we can notice that the symmetric nature gives the same key for any pair of nodes such that Kij = Kji |
| K= (D.H) mod 29 |
| The keys are assigned to sensor nodes before deployment and it is changed periodically by safeguarding from attacks. Specifically it is used for military purpose. |
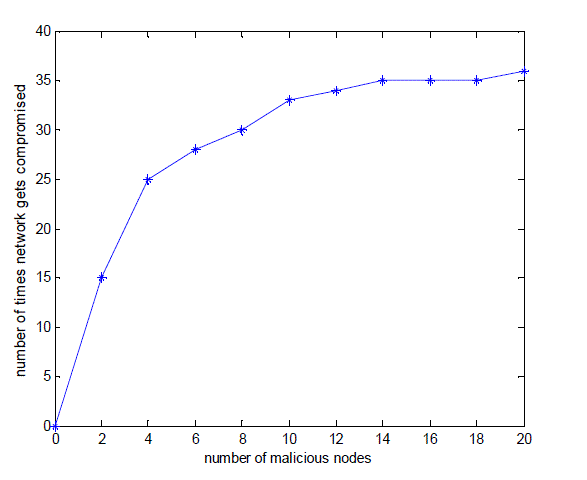
| The resiliency of the SHI-KPD scheme is shown in figure 3. It shows that number of malicious nodes is varied in x axis and the number of times the network gets compromised is performed. We infer that number of times the network gets compromised is around 36 for 20 malicious nodes. |
CONCLUSION
|
| This paper presents the comparative study of Hash function, Polynomial Pool, SBIDB, UNITAL, TRADE algorithms with the proposed algorithm the new way of generating the keys using the SHI-KPD scheme. The proposed method has the advantage of increasing the resiliency and connectivity than the existing scheme. In addition, this scheme provides more complex in computation thereby increases security. The result of SHI-KPD scheme is compared with other existing schemes and it shows that SHI-KPD scheme achieves more resilience over the network. |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
| |
References
|
- Eschenauer, L., &Gligor, V. D. (2002, November). A key-management scheme for distributed sensor networks. In Proceedings of the 9thACM conference on Computer and communications security (pp. 41-47). ACM.
- Chan, H., Perrig, A., & Song, D. (2003, May). Random key predistribution schemes for sensor networks. In Security and Privacy, 2003.Proceedings. 2003 Symposium on (pp. 197-213). IEEE.
- Blom, R. (1985, January). An optimal class of symmetric key generation systems. In Advances in cryptology (pp. 335-338). Springer BerlinHeidelberg.
- Ruj, S., Nayak, A., &Stojmenovic, I. (2011, April). Fully secure pairwise and triple key distribution in wireless sensor networks usingcombinatorial designs. In INFOCOM, 2011 Proceedings IEEE (pp. 326-330). IEEE.
- Du, W., Deng, J., Han, Y. S., Chen, S., &Varshney, P. K. (2004, March). A key management scheme for wireless sensor networks usingdeployment knowledge. In INFOCOM 2004. Twenty-third AnnualJoint Conference of the IEEE Computer and CommunicationsSocieties (Vol. 1). IEEE.
- Camtepe, S. A., &Yener, B. (2004). Combinatorial design of key distribution mechanisms for wireless sensor networks. In ComputerSecurity–ESORICS 2004 (pp. 293-308). Springer Berlin Heidelberg.
- Shaila, K., Manjula, S. H., Thriveni, J., Venugopal, K. R., &Patnaik, L. M. (2011). Resilience Against Node Capture Attack usingAsymmetric Matrices in Key Predistribution Scheme in Wireless Sensor Networks. International Journal on Computer Science &Engineering, 3(10).
- Subash, T. D., & Divya, C. (2011, December). Double hash function scheme in wireless sensor networks. In Information and CommunicationTechnologies (WICT), 2011 World Congress on (pp. 88-92). IEEE.
- Subash, T. D., & Divya, C. (2011, March). Novel key pre-distribution scheme in wireless sensor network. In Emerging Trends in Electrical and Computer Technology (ICETECT), 2011 International Conference on (pp. 959-963). IEEE.
|