International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Analysis of Quality Measurement Parameters of Deblurred Images

Dejee Singh1, R. K. Sahu 2
  1. PG Student (Communication), Department of ET&T, Chhatrapati Shivaji Institute of Technology, Durg, India1
  2. Associate Professor, Department of ET&T, Chhatrapati Shivaji Institute of Technology, Durg, India2
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Image blur is difficult to avoid in many situations and can often ruin a photograph. Image deblurring and restoration is necessary in digital image processing. Image deblurring is a process, which is used to make pictures sharp and useful by using mathematical model. Image deblurring have wide applications from consumer photography, e.g., remove motion blur due to camera shake, to radar imaging and tomography, e.g., remove the effect of imaging system response. In this paper we propose a method for image deblurring and reconstruction of HDR images using transformation spread functions (TSFs), which is directly estimated from locally derived point spread functions (PSFs) by exploiting their relationship. We are also calculating the quality Measurement parameters of images.

Keywords
Image deblurring, point spread function (PSF), transformation spread function (TSF), AD, MD, MSE,NAE, NK, SNR, SC etc.

INTRODUCTION
Images are obtained in areas ranging from everyday photography to astronomy, remote sensing, medical imaging, and microscopy. Unfortunately all images end up more or less blurry. This is due to the fact that there is a lot of interference in the environment as well as in the camera. The blurring or degradation of an image can be caused by many factors such as movement during the capture process, using long exposure times, using wide angle lens etc. Image deblurring is used to make pictures sharp and useful by using mathematical model. High dynamic range (HDR) imaging has become more and more popular in recent years. A few special cameras are available for capturing HDR images but they are still expensive and not prevalent. Images captured by hand-held cameras are likely to be blurry due to camera shake and with long exposures. This paper proposes a new technique to reconstruct a sharp HDR images and deblurring of that images. In this paper we propose a method for image deblurring, in which point spread function (PSF) has been estimated for a given blurry image. The process of deblurring an image typically involves two steps. First, it proposes a new approach to estimates transformation spread function (TSF). TSFs are estimated directly from point spread functions (PSFs), which specifies how the image is blurred. PSF is estimated from the blurry image itself, or alternatively using additional hardware attached to the camera. Second in addition to the estimation of TSFs, irradiance of an image is estimated. This method is then used for both blurred and non-blurred images.

LITERATURE SURVEY
There is an extensive literature on image deblurring, but here we mention just a few relevant papers on this topic. Many recent and successful image deblurring approaches are based on blind deconvolution [3]. In initial work of image deblurring we determine the camera response function [20] [23][13]. In this paper [13] imaging response function has derived and high dynamic range image has been recovered. Motion blur and noise are strictly related by the exposure time: photographers, before acquiring pictures of moving objects or dim scenes, always consider whether motion blur may occur (e.g., due to scene or camera motion), and carefully set the exposure time. The trade-off is between long exposures that reduce the noise at the cost of increasing the blur, and short exposures that reduce the blur at the cost of increasing the noise [9]. Tom Mertenset. al. proposed a technique to skip the step of computing a high dynamic range image, and immediately fuse the multiple exposures into a high-quality, low dynamic range image, ready for display (like a tone-mapped picture), called this process exposure fusion [21]. Mitsunaga and Nayar [14] assumed that the exposure ratios are initially unknown and that the inverse response function can be closely approximated by a polynomial. They then iteratively estimate the response and the ratios. The exposure of the camera is varied by changing either the aperture setting or the shutter speed. Sunghyun Cho et. al. has taken outliers such as saturated clipped pixels, non-Gaussian noise and non-linear camera response in to account and build a robust non-blind deconvolution method upon it, which can effectively reduce the visual artifacts caused by outliers [19]. Oliver Whyte has addressed the problem of deblurring images degraded by camera shake blur and saturated or over-exposed pixels [11] [12]. Lu Yuan et. al. has proposed a method of deblurring by using both blurred and noisy image [7]. Both the images the blurred and the noisy image are used to find an accurate blur kernel and reduce the deconvolution artifacts. Ankit Gupta et al. [2] have suggested that the camera motion can be modelled as a motion density function and the blur at each pixel can be obtained using this function. Ravi Kumar et. al. have presented the various quality metrics. Image quality assessment is closely related to image similarity assessment in which quality is based on the differences (or similarity) between a degraded image and the original, unmodified image.

METHODOLOGY
A. PSF Generation:
The PSFs constituting the collections of , which are used to compute the restoration error model [9]. PSFs defined as
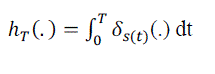image(1)
Where denotes the Dirac-Delta function and is motion blur PSF. S refers to PSF trajectory or simply trajectory. Each trajectory consists of the positions of a particle following a 2-D random motion in continuous domain. The particle has an initial velocity vector which, at each iteration, is affected by a Gaussian perturbation and by a deterministic inertial component, directed toward the current particle position.
Since > 0, then
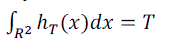image(2)
B. TSF Estimation:
The blur caused by camera motion is limited by six degrees of freedom of a rigid body motion, most commonly decomposed to three rotations and three translations [15]. A camera has 6 degrees of freedom viz. 3 translation and 3 rotation ).For hand-held cameras, variation is treated as negligible. , and are 3D transformation space [29].The final blurred intensity image in terms of the TSF can expressed as
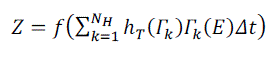image(3)
Where the value of hT(Γ) denotes the fraction of the total exposure for which the camera was stationary in the position that caused the transformation. We can write Z = f(KEΔt) where K is a large sparse matrix with the non-zero elements derived from TSF coefficients and bilinear weights. Δt denotes exposure time and E is irradiance of image. The local PSFs of a blurred image can be related to the TSF as [10][15]
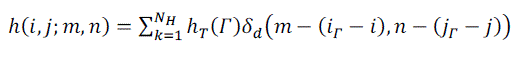image(4)
Where (iΓ,jΓ) denotes the position when transformation Γ-1 is applied on (i, j ), h is the PSF at (i, j ),and δd denotes the 2D kronecker delta function. If Np such PSFs are known, each PSFs can be related to the TSF as hpl=MlhT, where l=1…….Np. Ml is matrix whose entries are determined by location pl of the blur kernel and interpolation coefficients. The cost function to derive the TSF which is consistent with the observed blur kernels is given by
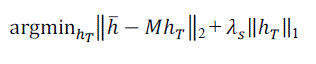image(5)
C. Quality Measurement Parameters:
MSE (Mean Square Error): The MSE is the average of the square of the difference between the desired response and the actual system output (the error). The mean square error (MSE) is one way to evaluate the difference between an estimator and the true value of the quantity being estimated. MSE measures the average of the square of the "error," with the error being the amount by which the estimator differs from the quantity to be estimated.
1) It is Defined as
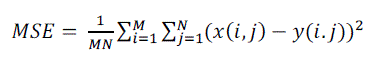image(6)
2) PSNR (Peak Signal to Noise Ratio): The term peak signal-to-noise ratio (PSNR) is an expression for the ratio between the maximum possible value (power) of a signal and the power of distorting noise that affects the quality of its representation. Because many signals have a very wide dynamic range, (ratio between the largest and smallest possible values of a changeable quantity) the PSNR is usually expressed in terms of the logarithmic decibel scale.
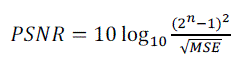image(7)
3) AD (Average Difference): This measure shows the average difference between the pixel values. Ideally it should be zero. It is defined as follows: -
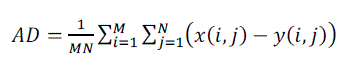image(8)
4) MD (Maximum Difference): Maximum Difference is defined as follows:
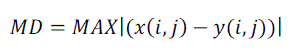image(9)
5) NK (Normalized Cross-Correlation): For image-processing applications in which the brightness of the image and template can vary due to lighting and exposure conditions, the images can be first normalized. It can be defined as:
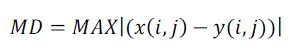image(10)
6) SC (Structural Content): The large value of SC means that image is a poor quality. SC is defined as follows:-
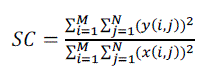image(11)
7) NAE (Normalized Absolute Error): The large the value of NAE means that image is poor quality.NAE is defined as:-
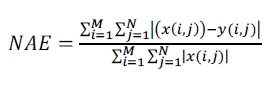image(12)

EXPERIMENTAL RESULTS
To evaluate the performance of proposed technique [15], we have used real image. For real images we have used NIKON D5 100 camera and captured the images on tripod to avoid motion blur. We have performed the algorithm in MATLAB (R2010a).
We have estimated the PSF trajectory, which defined the camera motion. In fig (c) we have shown the blurred image with different exposure times. In fig (d) left corner shows the estimated PSF trajectory curve and images show that the blur develops along trajectory
After estimating the PSFs, we have estimated the transformation spread function [10][29] for deblurring images. First we have performed algorithm on patches of blurred image. We have cropped four patches and then deblurred that patches.
Left side images are deblurred patch images using TSF and right side images are blurred patch images
After performing deblurring, we have calculated the quality measurement parameters [23] such as Mean Square Error (MSE), Peak Signal to Noise Ratio (PSNR), Peak Signal to Noise Ratio (PSNR), Peak Signal to Noise Ratio (PSNR), Structural content (SC), Maximum Difference (MD) and Normalized Absolute Error (NAE). The value of each parameter is shown in tabular form.

CONCLUSIONS
In this paper we discussed the deblurring method and quality measurement parameters. First we estimated the local PSFs or PSF trajectory curve. Trajectory curve defined the camera motion. After PSF estimation we performed the TSF on real image patches to deblur the images. We analyzed the quality metrics parameter such as PSNR, MSE, MD, AD, NK, NAE and SC. All parameters defined the quality of deblurred images and similarity measurement between original image and deblurred image.

Tables at a glance
Table icon
Table 1

Figures at a glance
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3

References
  1. J. Cai, H. Ji, C. Liu, and Z. Shen, “Framelet based blind motion deblurring from a single image,” IEEE Trans. Image Process., vol. 21, no. 2, pp. 562–572, Feb. 2012.

  2. A. Gupta, N. Joshi, C. Lawrence Zitnick, M. Cohen, and B. Curless, “Single image deblurring using motion density functions,” in Proc. ECCV,pp. 171–184, 2010.

  3. A. Levin, Y. Weiss, F. Durand, and W. Freeman, “Understanding blind deconvolution algorithms,” IEEE Trans. Pattern Anal. Mach. Intell.,vol.33, no. 12, pp. 2354–2367, Nov. 2011.

  4. Y. Tai, P. Tan, and M. S. Brown, “Richardson-Lucy deblurring for scenes under projective motion path,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 33, no. 8, pp. 1603–1618, Aug. 2011

  5. D. Kundur and D. Hatzinakos, “A novel blind deconvolution scheme for image restoration using recursive filtering,” IEEE Trans. Signal Process., vol. 46, no. 2, pp. 375-390, Feb. 1998

  6. L. Yuan, J. Sun, L. Quan, and H. Shum, “Image deblurring with blurred/noisy image pairs,” ACM Trans. Graph., vol. 26, no. 3, pp. 1–11,2007.

  7. Fergus, B. Singh, A. Hertzmann, S. T. Roweis, and W. T. Freeman, “Removing camera shake from a single photograph,” ACM Trans. Graph.,vol. 25, no. 3, pp. 787–794, 2006.

  8. Giacomo Boracchi and Alassandro Foi, “Modeling the performance of Image Restoration from Motion Blur”, IEEE Transactions on. vol.21, no.9, pp. 3952 - 3966 doi:10.1109/TIP.2012.2199324

  9. P. Chandramouli and A. N. Rajagopalan, “Inferring image transformation and structure from motion-blurred images,” in Proc. Brit. Mach. Vis.Conf., pp. 1–12, 2010.

  10. O. Whyte, J. Sivic, and A. Zisserman, “Deblurring shaken and partially saturated images,” in Proc. IEEE Workshop CPCV, ICCV, pp. 745– 752, Nov. 2011.

  11. O. Whyte, J. Sivic, A. Zisserman, and J. Ponce, “Non-uniform deblurring for shaken images,” in Proc. CVPR, pp. 491–498, 2010.

  12. T. Mitsunaga and S. K. Nayar, “Radiometric self -calibration”, in Proc. CVPR, pp. 1–7, 1999.

  13. C. S. Vijay, P. Chandramouli, and A. N. Rajagopalan, “HDR imaging under non-uniform blurring,” in Proc. ECCV Workshop Color Photometry Comput. Vis. , pp. 451–460, 2012.

  14. L. Zhang, A. Deshpande, and X. Chen, “Denoising vs. deblurring: HDR Imaging techniques using moving cameras,” in Proc. CVPR, pp. 522–529, Jun. 2010.

  15. M. D. Grossberg and S. K. Nayar, “Modeling the space of camera response functions,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 26, no. 10,pp. 1272–1282, Oct. 2004.

  16. M. D. Grossberg and S. K. Nayar, “Determining the camera response from images: What is knowable,” IEEE Trans. Pattern Anal. Mach. Intell.,vol. 25, no. 11, pp. 1455–1467, Nov. 2003.

  17. S. Cho, J. Wang, and S. Lee, “Handling outliers in non-blind image deconvolution,” in Proc. ICCV, pp. 495–502, 2011.

  18. S. Kim, Y. W. Tai, S. J. Kim, M. S. Brown, and Y. Matsushita, “Nonlinear camera response functions and image deblurring,” in Proc. CVPR,pp. 25–32, 2012.

  19. T. Mertens, J. Kautz, and F. Van Reeth, “Exposure fusion,” in Proc. Pacific Conf. Comput. Graph. Appl., pp. 382–390, 2007.

  20. S. Mann, R. W. Picard, “Being ‘undigital’ with digital cameras: Extending dynamic range by combining differently exposed pictures,” in Proc.46th Annu. Conf. IS&T, Soc. Imag. Sci. Technol., pp. 422–428, 1995.

  21. C. S. Vijay, P. Chandramouli and A. N. Rajagopalan, “Non-Uniform Deblurring in HDR Image Reconstruction,” IEEE Trans. on Image Processing, vol. 22, no. 10, October 2013.

  22. Ravi Kumar and Munish Rattan, “Analysis Of Various Quality Metrics for Medical Image Processing”, International Journal of Advanced Research in Computer Science and Software Engineering, Vol. 2 Issue 11 Nov. 2012