Keywords
|
| Cockcroft-Walton (CW) voltage multiplier. |
INTRODUCTION
|
| In generally to get high dc output voltage we are using voltage multipliers, DC-AC-DC inverters With step-up transformer due to using of transformers the size, cost and high ripples are present in output voltage and current. The Cockcroft–Walton (CW) generator, or multiplier, which is an electronic circuit it generates a high DC voltage from a low level input voltage AC or pulsing DC. Today Cockcroft-Walton (CW) circuits are still used in particle accelerators, and also in many electronic devices where high voltages require. The Applications are x-ray machines, television, and photocopiers. It is made up of ladder network of capacitors and diodes to generate high DC voltages. Here we are using only capacitors and diodes, these voltage multipliers can step up relatively low voltages to extremely high voltage, while at the same time lighter and cheaper than using step-up transformers. The biggest advantage of such circuits is that the voltage across each stage of the cascade is equal to only twice the peak input voltage in a half wave rectifier. It has the advantage of requiring relatively low cost components and easy to insulate. Possibility of taking output from any stage, like a multi tapped transformer. |
| LITERATURE SURVEY: Review of nonisolated high-step-up dc/dc converters in photovoltaic grid-connected applications,” by W. Li and X. He, IEEE Trans. Ind. Electron., vol. 58, no. 4, pp. 1239–1250, Apr. 2011. |
| How to achieve high-step-up, low-cost, and high-efficiency dc/dc conversion is the major consideration due to the low PV output voltage with the parallel-connected structure. Providing continuous input current with low ripple, high voltage ratio and low voltage stress on the switches, diodes and capacitors. |
| Cascaded dc-dc converter connection of photovoltaic modules,” by G. R. Walker and P. C. Sernia, IEEE Trans. Power Electron., vol. 19, no. 4, pp. 1130–1139, Jul. 2004. |
| Presents New residential scale photovoltaic (PV) arrays are commonly connected to the grid by a single DC-AC inverter connected to a series string of PV modules, or many small DC-AC inverters which connect one or two modules directly to the AC grid. |
PROPOSED CIRCUIT
|
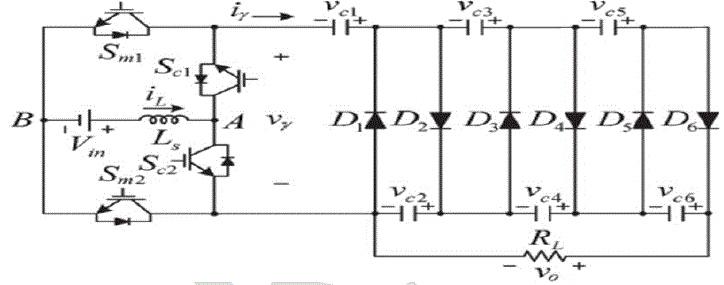
| In this paper, proposed converter supplied by a low-level dc source, such as battery, PV module, or fuel cells. The proposed converter (Cockcroft–Walton (CW) generator, or multiplier) consists of one inductor Ls(boost inductor), four switches (Sm1, Sm2, Sc1, and Sc2) the rating of all switches are same as well as voltage stress across each switches are same, and one n-stage CW voltage multiplier The four switches are divided into two groups Sm1 (Sc1) and Sm2(Sc2) which operate in complementary mode, and they are operating under two different frequencies of Sm1 and Sc1 are defined as fsm and fsc, respectively. For convenience, fsm is denoted as modulation frequency, and fsc is denoted as alternating frequency. The both fsm and fsc frequencies should be as high as possible so that we can use smaller inductor and capacitors in this circuit. In this paper, fsm (=60 kHz) is set much higher than fsc (=1 kHz), and the output voltage is regulated by controlling by the duty cycle of Sm1 and Sm2, while the output voltage ripple can be adjusted by fsc. As shown in Fig.1, the well-known CW voltage multiplier is constructed by a cascade of stages with each stage containing six capacitors (C1, C2, C3, C4, C5, C6,) and six diodes (D1, D2, D3, D4, D5, D6,). In an n-stage CW voltage multiplier, there are N (= 2n) capacitors and N diodes n=3 (3-stage). |
OPERATTION
|
| The operation of 3-stage Cockcroft-Walton (CW) Voltage Multiplier is divided to four mode operation is explained by the given below circuit diagrams from Fig. a to Fig. h |
| Mode 1: Sm1 and Sc1 Switches are turned on, and Sm2, Sc2 Switches turn off, and all diodes are turned off, as shown in Fig a. The boost inductor is get charged by the Vin which is may be fuel cell solar cell or other source, the even group capacitors C6, C4, and C2 are discharged and give supply to the load, the odd-group capacitors C5, C3, and C1 are not in conduction. |
| Mode 2: Sm2 and Sc1 Switches are turned on, Sm1 and Sc2 Switches are turned off, the current iγ is positive. The boost inductor (Ls) and input Vin dc source are in series the boosted energy transfer to the CW voltage multiplier through different even diodes, mode 2-A, diode D6 is conducting; the even-group capacitors C6, C4, and C2 are get charged, and the odd-group capacitors C5, C3, and C1 are discharged by iγ. Is Shown In Fig. (c), mode 2-B, diode D4 is conducting. Thus, C4 and C2 are get charged, C3 and C1 are discharged by iγ, C6 supplies load current, and C5 is floating. Is shown In Fig. (d), mode 2-C, diode D2 is conducting. Thus, C2 is charged, C1 is discharged by iγ, C6 and C4 supply load current, and C5 and C3 are not in conduction. |
| Mode 3: Sm2 and Sc2 Switches are turned on, and Sm1, Sc1, and all CW diodes are turned off, as shown in Fig (e). The boost inductor Ls is get charged by the Vin dc source, the even group capacitors C6, C4, and C2 supply the load current, and the odd-group capacitors C5, C3, and C1 are not in conduction. |
| Mode 4: Sm1 and Sc2 Switches are turned on, Sm2 and Sc1 Switches are turned off, and the current iγ is negative. The boost inductor Ls and input Vin dc source are in series the boosted voltage is “-Vγ” transfer energy to the CW voltage multiplier through odd diodes, mode 4-A, show in fig (f) diode D5 is conducting. Thus, the even-group capacitors, except C6 which supplies load current, are discharged, and the odd-group capacitors C5, C3, and C1 are charged by iγ. mode- 4-B, D3 is conducting. Thus, C2 is discharged, C3 and C1 are charged by iγ, C6 and C4 supply load current, and C5 is not in conduction. Is shown In Fig (g), mode-4-C, D1 is conducting. Thus, C1 is charged by iγ, all even capacitors supply load current, and C5 and C3 are not in conduction is shown In Fig (h). |
| The values and ratings of the components used in simulation circuit is given in table.1 |
SIMULATION AND RESULT
|
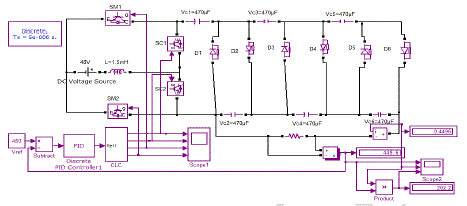
| In this chapter given obtained simulated results are presented for the closed loop analysis of 3-stage Cock-craft Walton (CW) voltage multiplier. |
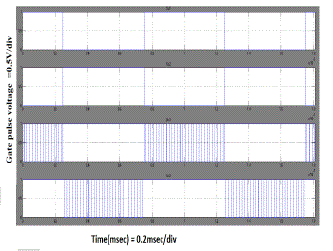
| In fig.4 shows the gate pulses for Sc1, Sc2, Sm1, Sm2.When Sc1 is on (1KHZ) Sc2 off and sm1 is operate at 60KHZ.Similiarly when Sc2(1KHZ) is on Sc1 is off Sm2 operate at 60KHZ. |
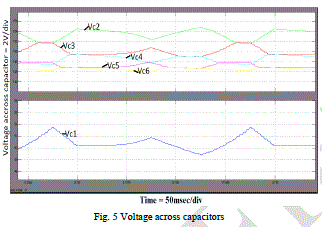
| In fig.5 shows the voltage across the each capacitor. The voltage across the capacitor C1 is less then the half of the remaning capacitors voltage. when odd capacitors (C1,C3,C5) are charging the even capacitors (C2,C4,C6) are discharging.Similiarly when even capacitors (C1,C3,C5) are discharging the odd capacitors (C2,C4,C6) are charging. Is shown in graph (fig.5).the voltage across the all capacitor is almost same (Except C1). We can select all capacitors at same rating. |
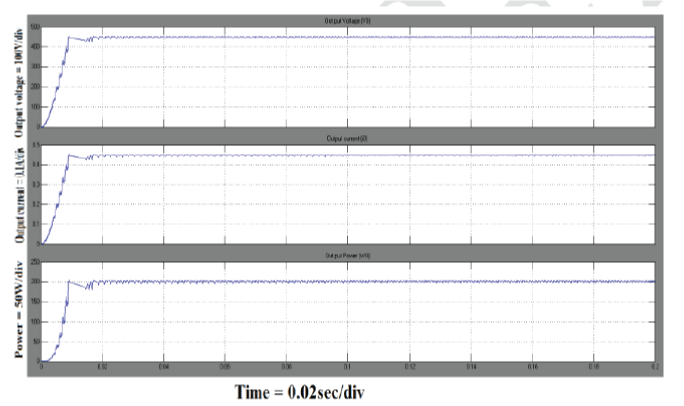
| These are simulated results obtained for the 3-stage Cockcroft-Walton (CW) voltage multiplier. The input voltage for Cockcroft-Walton (CW) generator is 48V, Output voltage is 450V, output current is 0.45Amp, and Output power is 200W. The output voltage range can be increased by adding the number of stages, for every stage we have to connect the two more capacitors and two more diodes. |
CONCLUSION
|
| In this paper, a high step-up dc-dc converter based on the Cockcroft-Walton (CW) voltage multiplier without using a transformer has been presented to obtain a high voltage gain. Since the voltage stress on the active switches, diodes, and capacitors is not affected by increasing the number of cascaded stages, power components with the same voltage ratings can be selected. The Control strategy employs two independent frequencies, one is operates at high frequency to minimize the size of the inductor(Ls) while the other one operates at relatively low frequency according to the desired output voltage ripple. Finally, the simulation and experimental results proved the validity of theoretical analysis and the feasibility of the proposed converter. In future we can increase number of n-stages the high dc output voltage can be converted to AC voltage. |
Tables at a glance
|
 |
| Table 1 |
|
| |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
 |
 |
 |
| Figure 4 |
Figure 5 |
Figure 6 |
|
| |
References
|
- B. K. Bose, “Energy, environment, and advances in power electronics,” IEEE Trans. Power Electron., vol. 15, no. 4, pp. 688–701, Jul. 2000.
- F. Blaabjerg,Z. Chen, and S. B. Kjaer, “Power electronics as efficient z interface in dispersed power generation systems,” IEEE Trans. PowerElectron., vol. 19, no. 5, pp. 1184–1194, Sep. 2004.
- Q. Li and P. Wolfs, “A review of the single phase photovoltaic module integrated converter topologies with three different dc linkconfigurations,” IEEE Trans. Power Electron., vol. 23, no. 3, pp. 1320–1333, May 2008.
- J. Wang, F. Z. Peng, J. Anderson, A. Joseph, and R. Buffenbarger, “Low cost fuel cell converter system for residential power generation,”IEEE Trans. Power Electron., vol. 19, no. 5, pp. 1315–1322, Sep. 2004.
- W. Li and X. He, “Review of nonisolated high-step-up dc/dc converters in photovoltaic grid-connected applications,” IEEE Trans. Ind.Electron., vol. 58, no. 4, pp. 1239–1250, Apr. 2011.
- L. S. Yang, T. J. Liang, and J. F. Chen, “Transformer less dc-dc converters with high step-up voltage gain,” IEEE Trans. Ind. Electron., vol.56, no. 8, pp. 3144–3152, Aug. 2009.
- G.R.Walker and P. C. Sarnia, “Cascaded dc-dc converter connection of photovoltaic modules,” IEEE Trans. Power Electron., vol. 19, no. 4,pp. 1130–1139, Jul. 2004.
|