International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

ANALYTICALLY COMPARISON BETWEEN LDPC- SC and LDPC-MRC USING GA APPROACH

Rekha Rani

Assistant Professor, Dept. of ECE, SSCET, Pathankot, Punjab, India

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Selection combining (SC) and maximal ratio combining (MRC) with Low Density Parity-check (LDPC) enhance the performance of overall system by providing coding gain. Using Gaussian approximation (GA) approach the bit error rate of LDPC-SC, LDPC-MRC system is derived for BPSK modulation over an independent and identically distributed (i.i.d) Rayleigh fading channel. The analysis is done for the case when the number of receiving antenna elements is varying from 3 to 6. In this paper, analytical result showed that at BER of 10-3, LDPC-SC and LDPC-MRC provide diversity gain 1.6 dB and 3 dB respectively when numbers of receiving antennas are varying from 4 to 6. So performance of LDPC-MRC is better than LDPC-SC and provides additional coding gain of 4.1dB and 1.7dB over uncoded SC and MRC systems respectively when N=6.

Keywords
Selection combining, maximum ratio combining, LDPC, GA

INTRODUCTION
In mobile communications, the quality of signal is degraded due to fading. By using spatial diversity technique, fading of the resultant signal is reduced and overall received SNR is increased. When error correcting code combined with spatial diversity technique then performance of the system is enhanced. So, Low-Density Parity Check (LDPC) codes which is invented by Gallager [1] are one of good error correcting codes which achieve good performance approaching Shannon limit by David Mackay[2]. In particular, an irregular LDPC code with optimum degree distribution achieves better performance than a regular LDPC code. The optimum degree distribution of the irregular LDPC code depends both on the channel and the system. The performance of LDPC Code with spatial diversity is analysed by Satoshi Gounai et al. [3]. Selection diversity combining employed in conjunction with LDPC by Beng Soon Tan et al. [4] which is able to mitigate the effects of fading. The probability of error of this scheme over i.i.d and i.n.i.d flat Rayleigh fading channel is derived using the extrinsic information transfer chart. Symbol error rate are derived for MRC and equal gain combining (EGC) diversity by A. Annamalai et al. [5] of multilevel quadrature amplitude modulation (MQAM) on arbitrary Nakagami fading channel. The bit error rate (BER) expressions of uncoded SC/MRC and SC/MRC with LDPC codes over an independent and identically distributed Rayleigh-fading channel are derived by Beng Soon Tan et al. [6] based on the Gaussian approximation approach. Kwok Hung Li et al. [7] proposed Lowdensity parity-check (LDPC) codes combined with cascade combining (SC/MRC and MRC/SC) which is able to achieve excellent bit-error rate (BER) performance over multipath fading channels. The BER expressions of cascade combining with and without LDPC codes over i.i.d. Nakagami-m fading channels are derived based on the GA approach.
The paper is organised as follows. First, Probability of error of uncoded selection combining (SC) and maximal ratio combining (MRC) is discussed. Next, Probability of error of coded selection combining (LDPC-SC) and maximal ratio combining (LDPC-MRC) is analysed. Then the results and discussion of combining are presented. Finally, the conclusion drawn is provided.

BER for UNCODED SC and MRC SYSTEM
For i.i.d Rayleigh channel, the PDF of SC and MRC for N branches is given by [8]
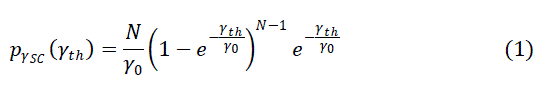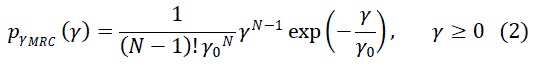image
image
where is the threshold signal to noise ratio (SNR), 0, average input signal to noise ratio of each branch which is equal to 2 , N number of receiving antennas.
To calculate gernalized average probability of error at the combiner is computed by integrating the probability of error in AWGN (additive white gaussian noise) channel over the i.i.d rayleigh distribution at the combiner which is given below
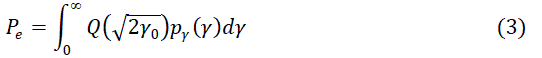image
So probability of error for SC over i.i.d rayleigh fading channel is by putting the value of equation (1) into equation(3) and then integrate
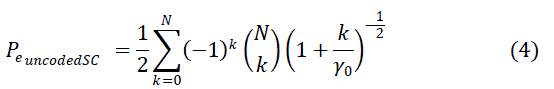image
Probability of error for MRC over i.i.d rayleigh fading channel is by putting the value of equation (2) into equation(3) and then integrate,
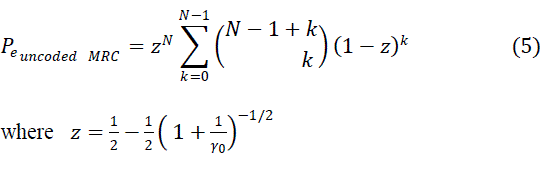image

BER for CODED SC and MRC SYSTEM
To calculate the BER of coded diversity combining techniques, Gaussian approximation method of LDPC is used. In GA method, assuming that all-zero codeword is transmitted for an AWGN channel with BPSK. To obtain the probability of bit error Pe of diversity combining with LDPC, integrate the PDF of variable node of designed system from -∞ to 0.
To calculate the PDF of variable node is to convolving the PDF of channel with the PDF of check node that is
image
First calculate the PDF of variable node by convolving PDF of channel LLR with PDF of check node, then integrate So, probability of error for LDPC-SC becomes
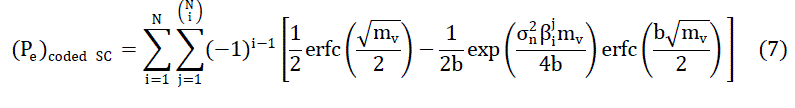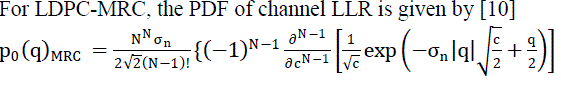image
image
where c = N + 1 2σn 2
Similarly, calculate the probability of error for LDPC-MRC
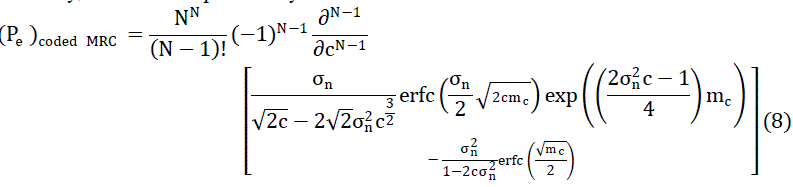image

RESULT and DISCUSSION
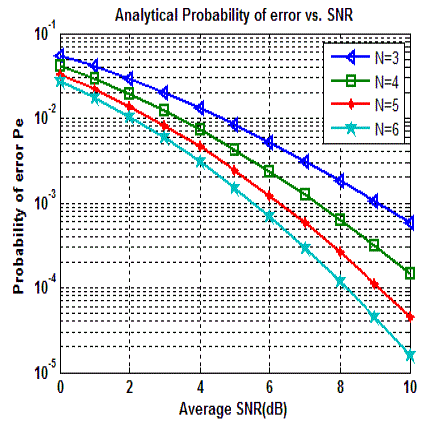
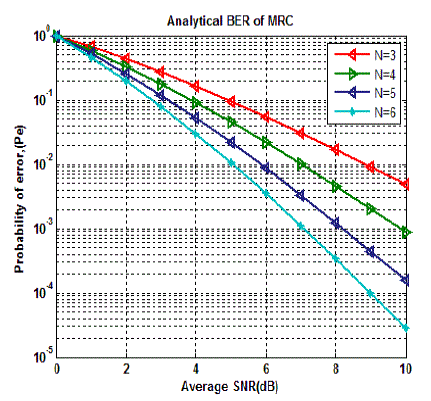
In this section, the analytical results for the SC, MRC, LDPC-SC and LDPC-MRC systems has been presented. For the uncoded SC and MRC systems, shown in Fig. 1 and Fig. 2 it is clearly observed that as the numbers of receiving antennas are raised, significant diversity gain is achieved. For uncoded SC and MRC, at BER of 10-3, an improvement of SNR 2dB and 3 dB are achieved respectively when number of receive antennas are increased from 4 to 6. So MRC is better than SC because at BER of 10-3 MRC improves 1dB SNR as compared to SC.
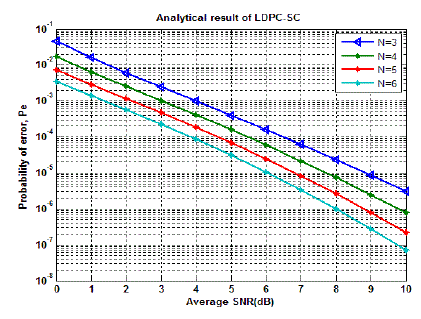
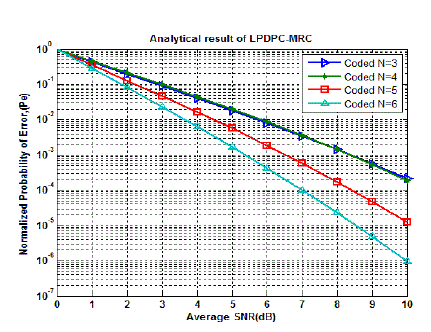
For coded SC and MRC systems, shown in Fig. 3 and Fig. 4 it is clearly observed that as the numbers of receiving antennas are raised from 4 to 6, at BER of 10-3, an improvement of SNR 1.6dB and 3 dB are achieved respectively.
A. Comparison between uncoded and coded systems
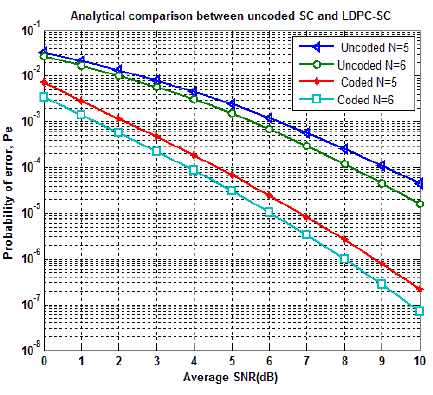
It is clear from the Fig. 5 that significant coding gain is achieved when comparing both the systems. At BER of 10-3, a coding gain of 4.1 dB is achieved by LDPC-SC system over SC system alone when the number of receive antennas are 6. So the performance of LDPC-SC is much better than the perfornance of SC because LDPC-SC requires less SNR around 4.1dB than SC.
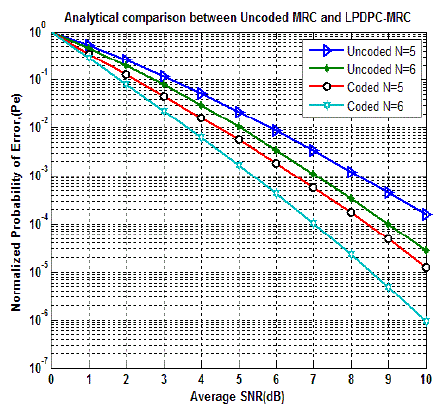
It is clear from the Fig. 6 that significant coding gain is achieved when comparing both the systems. At BER of 10-3, a coding gain of 1.7 dB is achieved by LDPC-MRC system over MRC system alone when the number of receive antennas are 6.

CONCLUSION
By using the Gaussian approximation approach, probability of error of uncoded and coded diversity combining systems over an i.i.d rayleigh fading channel has been derived. From the Numerical results, it is shown that coding combiner system gives the more optimistic results as compared to uncoded combiner system.

Figures at a glance
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3
Figure 4 Figure 5 Figure 6
Figure 4 Figure 5 Figure 6
 

References