Keywords
|
| wireless sensor network; Localization; TDOA; Artificial neural Network. |
INTRODUCTION
|
| Wireless sensor network (WSN) is a network of distributed self governing devices that can sense or monitor physical or environmental conditions. WSN can be deployed in a large area for monitoring environmental conditions, such as temperature, pressure, humidity, luminosity, air quality, soil property and also in battle field like target tracking, rescue operations. Most of the environmental sensing applications need to have location information of sensor nodes because sensing and processing data are meaningless without physical location of the sensor nodes. Many communication protocols of the WSNs are also based on the location information of the sensor nodes such as geographical routing protocol, Location based Energy-Aware Reliable routing protocol (LEAR), and more over location itself is often the data that needs to be sensed. Approximately all applications of WSNs need information about the physical location of the sensor nodes. |
| Number of techniques has been proposed for WSN node location estimation. One method to determine the location of nodes is through manual configuration, which is not feasible for large scale deployment. Another method is Global Positioning system (GPS), but GPS system is high hardware cost and power constraint, if we deploy them on every node and also it is not good for indoor environments. In general only few numbers of nodes positions are measured by GPS. |
| Another way of node localization methods are by Range based and Range free methods. Range based methods relies on distance measurements between nodes. There are many techniques for the estimation of distance or angle between the nodes. Some general techniques are Angle of Arrival, in this method the estimation of the angle is done by using directive antennas. Experiments show that this method has an inaccuracy of some degrees about 5°. In the second method, Received Signal Strength, the signal which is from sender node to receiver node can be highly influenced by noise, obstacles, and the type of antenna used. Third method is Time of Arrival (TOA), Time Difference of Arrival (TDOA) to estimate distance between anchor nodes and sensor nodes. In TOA method there should be time synchronization between all anchor and sensor nodes, in practical scenario it is difficult to achieve. In this paper proposes, TDOA method for node localization using neural network. This method does not require time synchronization between anchor and sensor nodes and also it is good in line of sight system (LOS). |
RELATED WORK
|
| The authors of paper [1] compared different techniques Hop Count, TOA, TDOA, and RSS. He found that TDOA method of distance measurement has high accuracy in LOS and NLOS than RSSI, TOA and hop count. But its hardware requirement is more than other three. The limitations associated with previous methods, we proposed an algorithm based on TDOA approach for distance measurement between anchor and sensor nodes. This is combined with feed forward back propagation neural network model, radial basis function neural network and multi layer perceptron network for prediction of sensor node’s position. |
| In paper [2], authors had done a survey on computational artificial intelligence paradigms for wireless sensor networks. In case of node localization they found genetic algorithm and artificial neural networks more appropriate than other computational intelligence methods. |
| In paper [6], a new kind of algorithm for node localization using multilayer perceptron neural network (MLP) was proposed. The authors used received signal strength (RSS) technique to estimate the distance between the sensor nodes and the anchor nodes. Their simulation results showed that the location accuracy is directly proportional to the number of access points (APs). |
| In paper [7], authors proposed a multilayer neural network model called artificial synaptic network (ASN). Distance was estimated on the basis of time of arrivals (TOA) method. They also applied the same problem to MLP and RBF neural network models and found the proposed ASN model better in terms of RMSE, number of iterations and memory requirement. |
| In paper [8], authors showed two algorithms based on ANN. One is MLP with only one hidden layer and other is MLP with two hidden layers. Their simulation result showed that the performance of MLP with two hidden layers is better than MLP with one hidden layer. |
PROPOSED METHODS
|
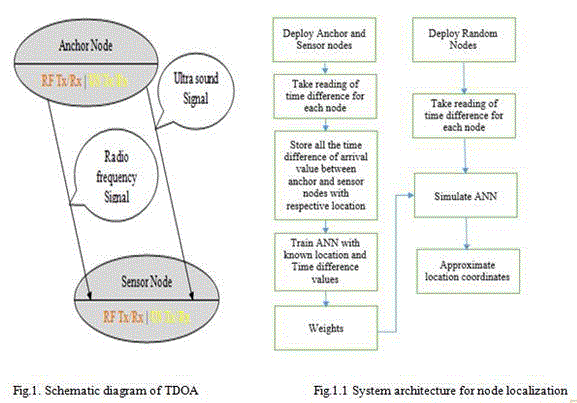
| A schematic diagram of distance calculation between the sensor node and anchor node using TDOA is shown in Fig.1. and system architecture is shown in fig 1.1 In TDOA, the Anchor node sends a radio signal and ultra sound signals to sensor node, sensor node note downs the current time TRF and TUS. Propagation speed of radio is faster than ultra sound in air, so both signals reach to sensor node at different time delay. This time difference of arrival is used to calculate the distance between anchor node and the sensor nodes by using |
| D= (SRF-SUS)*(TRF-TUS) (1) |
| Where SRF indicates propagation speed of radio frequency, SUS indicates propagation speed of ultra sound signal, TUS and TRF indicates arrival times of both radio signal and ultra sound signal respectively, D is a distance between anchor node and sensor node in meters. |
| A. Artificial neural network: |
| Neural networks are modeled resembling the biological neuron system. Artificial Neural Networks (ANNs) are the important components of Computational Intelligence. It is the network of interconnected nodes, termed ‘Neurons’, with linear or nonlinear active functions. Neural networks are divided into three categories according to their learning process those are Reinforcement learning, supervised learning, Unsupervised Learning Networks. In this proposed model we are using Radial Basis function Network model and Multilayer perceptron, it comes under supervised learning Networks. |
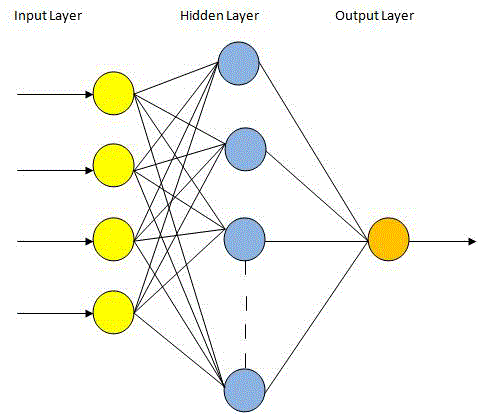
| B. Radial basis function network (RBFN) |
| Radial Basis Function Networks (RBFN) consists of 3 Layers – an input layer, one hidden layer and an output layer. The hidden units offer a set of functions that form an arbitrary basis for the input patterns. It has only one hidden layer as shown in Fig.2. |
| The hidden nodes implement a set of radial basis functions (Gaussian functions). The output nodes implement linear summation. The net input of a radial basis neuron is different from that of other neurons. Here the net input to the radial basis transfer function is the vector distance between its weight vector and the input vector, multiplied by the bias. The radial basis function has a maximum value is one when its input is zero. As the distance between weight vector and input vector decreases, the output increases. |
| C. Multi layer perceptron Network (MLP) |
| The perceptron computes a single output from multiple inputs by forming a linear combination according to its input weights and then put the output through nonlinear activation function. The activation function is chosen to be the logistic sigmoid function. Multilayer perceptron network is trained by repeatedly passing forward the input through the network. The weights are updated based on the difference between the desired output and the actual output of the network. Final weights of the Multilayer perceptron network completely depend on the initial weights. |
DATASET PREPARATION
|
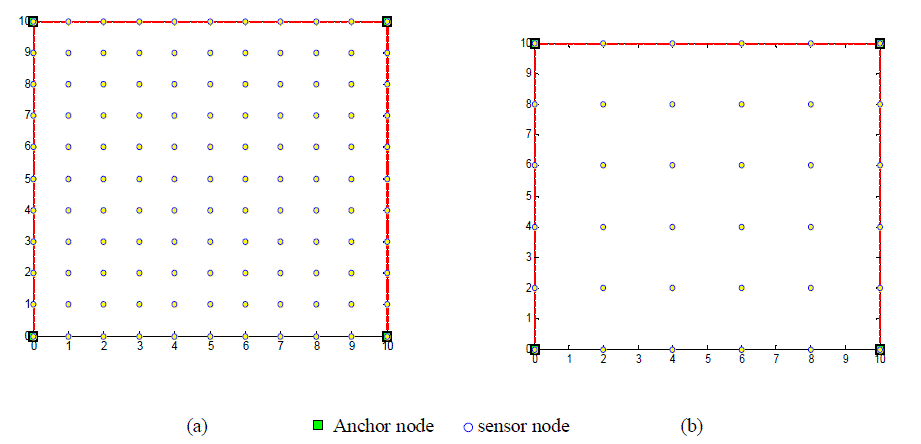
| Data sets were generated by using MATLAB. Two training data sets have created, one is of 121 data points and other is of 36 data points (Sensor nodes) which are uniformly distributed over a square area of 10m x 10m. Each data set consists of four anchor node at the corner of the square area. The distance of each data points (Sensor node) from all four anchor nodes were calculated in MATLAB using TDOA. These distance information were given as input values and co-ordinates of x and y values of each sensor node were given as a target values to the neural network models for training. Fig.3. shows training Data sets. Other 50 data points have been generated randomly for the testing data set. Data set for testing is shown in Fig.4. |
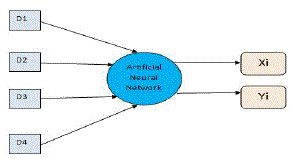
| For testing; TDOA information data were given as input to the neural network models and coordinates x and y of the nodes were taken as the outputs as shown in Fig. 5. |
| In Fig. 5, D1, D2, D3 and D4 are the distances from 1st, 2nd, 3rd and 4th anchor nodes respectively to the ith sensor node (data point). After obtaining the nodes coordinates, calculate the root mean square error to check the accuracy of estimated nodes and the performance of the models by using question 1. |
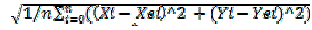 (1) (1) |
| Where, xi, yi are the actual coordinates of the ith data Point and xei, yei are the estimated coordinates of the ith data point by the network. |
SIMULATION RESULTS
|
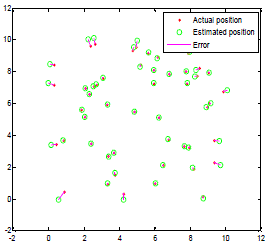
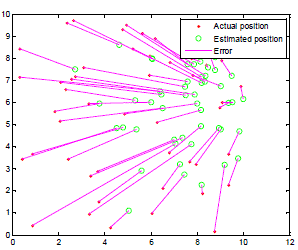
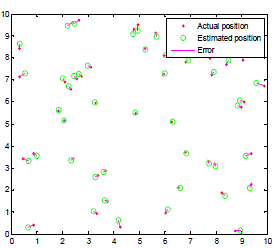
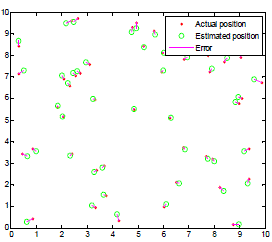
| For Radial basis neural network model with 50 hidden neurons in the hidden layer was trained with 121 training data set and for testing purpose we trained with 50 training data set as shown in fig.4, from where a root mean square error of 1.378642 m was calculated. After that this network was trained with 36 data points. This was again tested with the same dataset and it generates a root mean square error of 21.815630m. The actual position and estimated position of each node for both cases are shown in fig.6 and fig.7. |
| multi-layer perceptron network model was trained by using 121 dataset and after testing it with test data set we got root mean square error of 1.258346m. Again multi-layer perceptron was train with 36 dataset and test with test data sets the outcome was root mean square error of 1.276742m. The actual position and the estimated position of each node after simulations for both the cases are shown in Fig. 8 and Fig.9. |
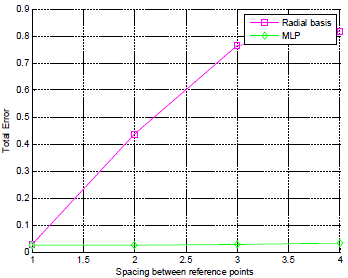
| The same process was repeated for different density training data points’ dataset. Table 1 and Fig. 10 show the comparative performance results of localization error for ANN (Artificial Neural Network) models. |
CONCLUSION AND FUTURE WORK
|
| The purpose of this study is how to localize the nodes by using TDOA and estimate the location errors by using two artificial neural models with respect to root mean square error, when both the models were trained with low and high density of data points. In this paper gives a brief idea about performance analyses of both Radial Basis function Network model and Multilayer Perceptron Network model. |
| Simulation results showed that, when there is lower density nodes grid the root mean square error value of Radial Basis Function Network model exponentially increases, if there is higher density node grid, root mean square error is gradually decreases. In the case of MLP when node density increases or decreases the localization error is comparatively lesser than RBFN hence MLP gives better performance on both the conditions. |
| This work can be extending for non-line of sight condition (NLOS). Currently we worked on two dimensions but it can be implement on three dimensions. |
Tables at a glance
|
 |
| Table 1 |
|
| |
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
Figure 10 |
|
| |
References
|
- S. B. Kotwal, Shekhar Verma, R.K. Abrol, “Approaches of Self Localization in Wireless Sensor Networks and Directions in3D,”International Journal of Computer Applications (0975 – 8887) Volume 50 – No.11, July 2012.
- Raghavendra V. Kulkarni, Anna Förster, and GaneshKumar Venayagamoorthy, “Computational Intelligence in Wireless Sensor Networks: A Survey,” VOL. 13, NO. 1, FIRST QUARTER 2011.
- Shareef, Yifeng Zhu, Mohamad Musavi, and Bingxin Shen, “Comparison of MLP neural network and kalman filter for localization in wireless sensor networks,” In Proceedings of the 19th IASTED International Conference on Parallel and Distributed Computing and Systems, pp. 323–330. ACTA Press, 2007
- Ergut S., Rao R.R., Dural O. and Sahinoglu Z. “Localization via TDOA in a UWB Sensor Network using Neural Networks,” Publication Year: 2008, pp. 2398 - 2403.
- Sayed Yousef Monir Vaghefi, Reza Monir Vaghefi “A Novel Multilayer Neural Network Model for TOA-Based Localization in Wireless Sensor Networks,” Proceedings of International Joint Conference on Neural Networks, San Jose, California, USA, July 31 – August 5, 2011 pp. 3079-3084.
- M. Gholami n, N.Cai, R.W.Brennan “An artificial neural network approach to the problem of wireless sensors network localization,” Robotics and Computer-Integrated Manufacturing 29 (2013), pp. 96–109.
- Kuldeep Singh and Sunil Agrawal, “Comparative Analysis of five Machine Learning Algorithms for IP Traffic Classification,” in IEEE International Conference on Emerging Trends in Network and Computer Communication (ETNCC-2011), Udaipur, pp. 33-38, April 22- 24, 2011.
- Prince Sing and Sunil Agarwal “TDOA Based Node Localization in WSN using Neural Networks” International Conference on Communication Systems and Network Technologies, 2013 IEEE.
- Shruti Gujral and Sunil Agrawal, “A Performance Comparison of Four Machine Learning Algorithms for Text Dependent Speaker Recognition Using Prosodic Features,” in CAN’2012 Eleventh AES-ATEMA’2012 international conference on Advances and Trends in Engineering Materials and their Applications, Toronto, Canada, pp. 165-172, August 06-10, 2012.
- Sunil Agrawal and B.S.Sohi, “Off-line Analysis of Internet Traffic for Accurate Identification of P2P Applications using Neural Networks,” IEEE International Conference on Recent Advances in Information Technology (RAIT – 2012), ISM, Dhanbad, pp. 431-435, 15-17 March 2012.
|