ISSN:2321-6212
ISSN:2321-6212
Abduljelili Popoola1*, Gbadebo I Olaton2, Ismail A. Buliyaminu1
1 Department of Physics, King Fahd University of Petroleum and Minerals, Dharhan, Saudi Arabia
2 Department of Physics, Osun State University, Osogbo, Nigeria
Received: 02-Jul-2021, Manuscript No. JOMS-21-001-PreQc-22; Editor assigned: 05-Jul-2021, PreQC No. JOMS-21-001-PreQc-22 (PQ); Reviewed: 19-Jul-2021, QC No. JOMS-21-001-PreQc-22; Revised: 19-Jul-2022, Manuscript No. JOMS -21-001-PreQc-22 (R); Published: 20-Sep-2022, DOI: 10.4172/2321-6212.10.7.005.
Visit for more related articles at Research & Reviews: Journal of Material Sciences
In this work, a model for computing the economic thickness of cooking pots of any shape was formulated based on Fourier’s law of heat conduction. In addition, the effect of varying thermal conductivity and sizes of the aluminum pots on its economic thickness was investigated. The cost of heating per year and the economic thickness of 5500 L pure aluminum pot were estimated to be £145.8325 and 9.00 mm, respectively. The cost of heating per year reduces by 2.5% while the economic thickness of the pot increases by 92.0% for aluminum pot alloyed with 8% by mass of Lithium metal. The most outstanding characteristic of the model was its ability to predict the economic thickness behavior of insulators, conductors and highly conducting materials with respect to the thermal conductivity, thereby giving distinction between the three classes of materials. Finally, an approximate balance was found between cost of heating through pot’s thickness and its cost of production, leading to conservation of both energy and resources.
A model; Aluminum cooking pots; Aluminum-Lithium alloy; Economic thickness; Thermal conductivity
The term “energy conservation” is still a highly discussed topic among the population of the world. Although this phrase may not be a mere conjure of alien words to the population of the developed countries. Perhaps, it is a strange mix of words amidst the population of developing countries that are still battling with other problems such as insecurity, flooding, unstable power supply, unsafe drinking water, mismanagement of resources etc. The fact that the developing countries, like Nigeria, are still struggling with stable power supply is the more reason wise use of energy among the population of these countries is important. On average, more than half of a country’s total energy supply is channeled towards cooking [1,2]. Therefore, there is a need to control the amount of energy used while cooking. This is needed especially in the developing countries where energy wastage cannot be condoned. To control the energy consumption while cooking, one needs to take a deep insight to factors affecting the energy usage while cooking. Some of these factors include energy source, nature of cooking pot, the type of food etc. There are many thermal energy conversion appliances including hot plates, induction cooker [3], local stoves [4-6] etc. which can be used for cooking. Few research works were aimed at minimizing energy lost from these thermal energy conversion appliances during cooking [6-9]. However, majority of the population of developing countries use local stoves. Therefore, many research works have been conducted on ways to improve the efficiencies of these local stoves, health regrets of using these stoves etc. Not many research works, as far as we know, has been carried out on ways to minimize energy usage by tuning the properties of pot used for cooking. The most common type of pot used for cooking among the populations of these developing countries is the so-called cast aluminum pot [10]. The pot is usually made from recycling of different scrap of metals from electronic waste, engine parts, old pots and abandoned kitchen utensils etc. These scraps of metals are subjected to a very high temperature, far beyond their melting point. At this molten state, the molten form is made into any desired shape of pots. Pots made in this way are not anodized. Metallic elements, with which the pots were made, are free to migrate. Hence, these free metals may contaminate the food. Thus, anodized pots are safer to use for cooking. Therefore, anodized pots commonly used among middle class population will be one of the pivots of this research work. To minimize the energy consumption during cooking, Olatona and Alamu developed a model for estimating the optimum thickness of clay pots in 2014. In 2015, Olatona and Popoola extended the concept to develop another model which computes the optimum thickness of a certain shape of cast aluminum pots. In both cases, the major concern was to find a particular thickness at which the cost of heating through the pots’ thickness is minimized. Therefore at this thickness, both cost and energy are optimized leading to wise use of energy and resources.
Herein, we present a modified model for determining the economic thickness of aluminum pot and investigating the effect of decreasing thermal conductivity of aluminum on the economic thickness of these pots. This lowering of thermal conductivity will be achieved by alloying aluminum with metals of lower thermal conductivity. For this, we used for the demonstration lithium. Thermal conductivities of aluminum and lithium are 237 W/(m.K) and 85 W/(m.K), respectively. Therefore, alloying aluminum with lithium will lower the thermal conductivity of aluminum. Our work will therefore be focused on investigating the effect of this kind of alloying on the economic thickness of two different shapes of aluminum pots. The pot’s shape to be considered are anodized open cylindrical pot and un-anodized approximately cylindrical top spherical frustrum aluminum cast pots.
Mathematical formulation of the model
To develop the model, we followed the procedure reported by Olatona and Popoola. However, in this case, we are interested in more common type of cooking pots i.e. the anodized open cylindrical shape aluminum pots. Among other unique characteristics of the model are its ability to distinguish between classes of material based on the economic thickness behavior, prediction of the economic thickness of pots based on only the size of pot, prediction of the particular value of thickness and radius at which both energy and resource are most wisely spent and its applicability to pots of any shape, size and material composition. This model, if employed by potters in pots production, may scale up towards building energy, cost and resources saving kinds of pots, supporting the global aim of energy and resources management. (Figures 1a and 1b)
Taking conduction as predominant heat transfer to the pot, Fourier’s law becomes applicable. The law can be stated as shown in Equation (1), where Q, k, A, dt, dx are rate of heat transfer to the pot, thermal conductivity of the pot, total surface area of the pot, temperature difference between the inner and outer surfaces of the pot and thickness of the pot, respectively.
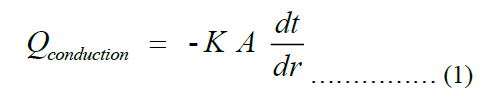
Next, we get an explicit expression for the thickness of the pot. The cross-section view of the pot is shown in Figure 2 below.
The total surface area of an open cylindrical shape shown in Figure 1b is given by Equation (2) below.
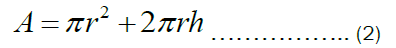
Let the radius of the pot, r equals the height of the pot, h. Therefore, Equation (3) can be rewritten as:
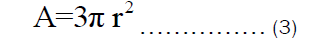
The volume of the open cylindrical pot shown in Figure 1b can be rewritten as:
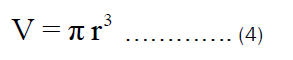
Substituting Equation (3) into Equation (1), we get:
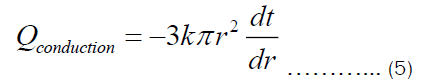
Integrating Equation (5) with respect to r from r1 to r2 and with respect to t from t1 to t2, we get
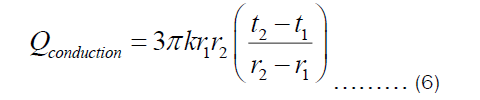
If the thickness of the pot is denoted by X=r2-r1, then Equation (6) becomes:
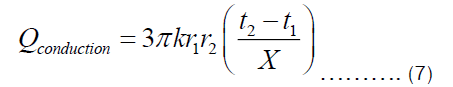
There are two ways in which heat is being transferred from the heat source to the item being cooked in the pot. One is conduction through Fourier transfer, which has been applied to get Equation (7). Another is the heat transferred from the inner surface of the pot to the food being cooked in the pot. The later happens through convection since most food requires fluids for its preparation. The heat transferred through convection can be represented by Equation (9), where U and ΔT are heat transfer coefficient and temperature difference between the inner surface of the pot and item inside the pot, respectively.
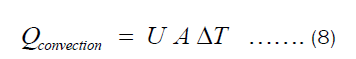
Substituting Equation (3) into Equation (8), we get:
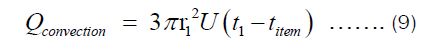
Assuming energy is conserved, Qconduction = Qconvection. Using this, we get:
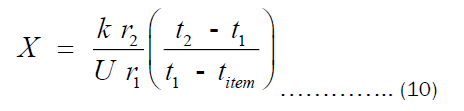
Equation (10) is the expression for estimating the thickness of the pots. However, we are interested in the economic thickness. This then bring cost analysis into the picture. It is important to declare that Equation (10) is surface area- independent, which means that the thickness of all pots of different shapes can be obtained via the same equation. Olatona and Popoola didn’t realize the later fact. The cost of heating the pot per year is the sum of cost of transferring heat from the heat source to the pot (Chs) and cost of transferring heat through the pot’s thickness to the item inside the pot (Cpt). Mathematically, the total cost of heating may be written as Equation (11).
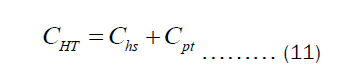
The Chs and Cht depend on the heat transfer through convection and pot’s thickness, respectively. They may be written as Equations (12) and (13).
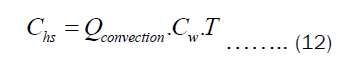
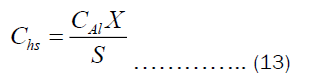
Substituting Equations (9) and (10) into (12) and (13), respectively. Then substituting the resulting equation into (11), we get Equation (14).
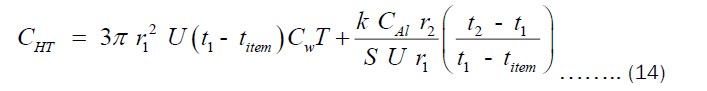
The CHT can also written in term of the thickness “X” as shown in Equation (15).
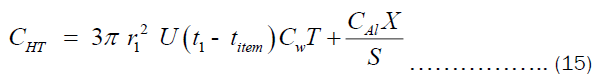
From Equation 10, t1 may be written as given by Equation 16.
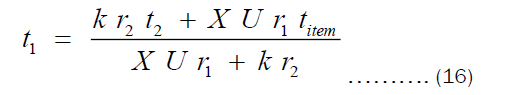
Substituting Equation (16) into (15) and considering also that X = r2 - r1, we get:
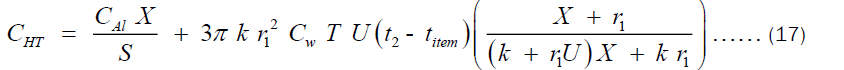
Where CAl, CHT, X, S1, r1, U, Cw, T, k, titem and t2 are the cost per unit volume of aluminum, cost of heating through the pot’s thickness, thickness of the pot, life span of the pot, internal radius of the pot, Total heat transfer coefficient, cost of wood equivalent to 1 J of heat, total time of operation of the pot per year, thermal conductivity of the pot, temperature of the food inside the pot and temperature of the outer surface of the pot, respectively. It is worthy to mention here that Equation (17) was the same equation obtained by Olatona and Popoola for the economic thickness of aluminum pots of shape shown in Figure 1a. After trying to formulate another model for aluminum pot of shape shown in Figure 1b, the deduction is that the model happens to be the same. This is an indication that the model is independent of the size, shape or volume of pot but rather on the material composition of the pot. This implies the economic thickness of pots can be tuned by tuning some intrinsic property of the pot such as the thermal conductivity. An obvious dependence of cost of heating through the pot’s thickness on the thermal conductivity of the cooking pot is shown in Equation (17). Hence, an attempt to change the thermal conductivity definitely affects the pots thickness and its heating cost. Hence, we can determine the exact economic thickness at which the cost of heating through the pot’s thickness is minimal.
The parameters used for computing the CHT include: titem=100°C (since most food are cooked at or beyond the boiling point of water), t2=127.83°C (temperature of the external surface of the pot, especially the side in contact with the heat source), r1=0.098 m, r2=0.100 m, CAl=1250 Naira/Kg (cost of aluminum per kilogram), S1=5 yrs (provided the pot can last for about 5 years), T=1460 hrs/yr (most people cook three times a day. If an average time to cook one meal is 1 hour. Then, we assume that the total time for pot’s usage per day is 4 hours), Cw=20.00 Naira (If the local stove is the heat source, then that is the price of firewood equivalent to 1J of heat), U=200 W/(m2.K) (heat transfer coefficient of water is between 230-280 W/(m2.K), we chose 200 W/(m2.K) because other constituents of the food may tend to lower its heat transfer coefficient).
Proceeding from Equation (17), the economic thickness can also be interpreted as the value of x for which cost of heating is minimum. Therefore, we evaluate x at the point where the derivative of CHT with respect to x is zero. The result of this is shown in Equation (18).
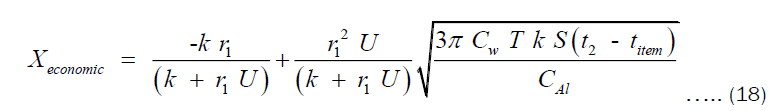
Where Xeconomic is the economic thickness of the pot. Using Equation (18), the economic thickness of pots of any volume can be estimated. The economic thickness depends on the thermal conductivity of material. Therefore, the model is not limited to only aluminium pots but pots made of any material.
Computation
Many research works have been done on alloying of aluminum with different metals such as silicon, Lithium, copper, zinc etc. For that we have various types of aluminum alloys such as 3003, 360, 1050A, 6060, 6061, 6063 etc. However, very few researchers have worked on alloying of aluminum with just a single metal, example of which is a case of aluminum-lithium alloy. Therefore, we shall make use of an already available data in the literature on the determination of thermal conductivity of different percentage of lithium in aluminium-lithium (Al-Li) alloy. The data used in our computation was reported by L. P Costas. The respective thermal conductivity values, shown in Table 1, were measured at different temperature ranges. The authors declared that the values are strictly correct within the stated temperature ranges in Table 1. These temperature ranges may also be narrowed down to the mean temperature. This assertion is necessary considering the dependency of temperature on thermal conductivity of metals. We compute Equation (17) and (18), using a C++ compiler (dev cpp 4.9.9.2 compiler) to determine the economic thickness of aluminum pot. The computation was performed with the reported values of thermal conductivities in Table 1, the model represented by Equation (17) and (18), and the aforementioned parameters.
| % of lithium in Al-Li alloys | k (W/(m.K) | Mean temperature (°C) |
|---|---|---|
| 0 | 250.62 | 127.2 |
| 1.07 | 137.65 | 196.7 |
| 1.4 | 109.62 | 199.5 |
| 2.3 | 104.6 | 185 |
| 4.77 | 79.08 | 181.1 |
| 7.94 | 66.11 | 176.6 |
Table 1. Thermal conductivities of different percentages of Lithium in Al-Li alloys.
Variation of thermal conductivity and economic thickness with respect to the percentage by mass of Lithium in Al-Li alloy is shown in Figure 3a. A clearer representation through bar chat is also shown in Figure 3b. As seen in these Figures, thermal conductivity decreases as the percentage by mass of lithium increases. This is due to the increase in quantity of heat carriers which results from alloying aluminum with Lithium. Usually, electrons are heat carriers in conductors and the motion of these electrons are impeded by other electrons when more electrons take part in the conduction. This might lead to increase in electron-electron collision, which decreases the effective number of heat carriers.
So, alloying aluminum with lithium is a tantamount to introducing more electrons to the aluminum material. This reduces heat conduction which in turns lowers the thermal conductivity of the Al-Li alloy. As shown in Figures 4a and 4b, the thickness at which the cost of heating is most minimized is taken as the economic thickness of the pot. Hence, the economic thickness does not literally imply “the smallest thickness”. It means the thickness to be considered for production of pots which will ensure an economic use of energy. This saves the pots’ users some money and also saves the country in her efficient energy usage.
Figure 4: (a) The plots of cost of heating versus thickness of aluminum pot alloyed with 0% Lithium; the thickness at which the cost of heating is minimum is taken as the economic thickness (b) The plots of cost of heating versus thickness of aluminum pot alloyed with 1.07%, 1.4%, 2.3%, 4.77% and 7.94% Lithium, corresponding to different thermal conductivity values.
An increase in economic thickness and decrease in the cost of heating with respect to the increase in percentage of Lithium in the Al-Li is shown in Figure 5.The economic thickness is a parameter that is determined based on the value of the minimum cost of heating.
Therefore, the reason for the observed decrease in cost of heating with respect to the decrease in thermal conductivity needs to be explained before the later can be interpreted. For thin pots made from material of high thermal conductivity, the rate of heat transfer through the pot’s thickness is almost the same as rate at which heat is being lost to the surrounding.
This is true since a better absorber of heat is also a better emitter of heat (Kirchorff’s law). The thermal conductivity, a Fourier’s law’s constant, of material is the ability of the material to transfer heat. As the thermal conductivity decreases, the heat retention ability increases since the rate at which the pot loses heat is less than the rate at which the pot gains heat. Hence, the effective heat transfer to the item inside the pot increases.
Therefore, less amount of energy will have to be converted to thermal energy. This directly explains the reason for the observed reduced heating cost shown in Figures 4 and 5.
Because there is a particular point at which the cost of heating must be minimum, all other necessary parameters must re-adjust their values such that the insulation property of the pot is enhanced. Thus, the economic thickness increases as thermal conductivity decreases. These two factors combine to increase the effective heat transfer to the item inside pot while cooking. As the thickness increases with decreasing thermal conductivity, the insulation property of the pot enhances such that the rate of gaining heat energy by the pot is more than the rate at which the pot loses heat energy. This eventually leads to lowering cost of heating as explained earlier.
The dependence of the thermal conductivity and outer radius of the pot observable in Equation (18) has also been represented graphically in Figures 6a and 6b. The graph of economic thickness versus thermal conductivity was plotted for low, high and ultra-high thermal conductivity. Between around 0 to 22 W/(m.K) thermal conductivity values, economic thickness increases till a maximum point is reached where the economic thickness again begins to decrease, mimicking the same pattern reported by Mahlia et al at very low temperature. This decrease in the economic thickness continues till around 500 W/(m.K) where the economic thickness values begin to remain constant.
From 0 to 22 W/(m.K), the economic thickness increases as the thermal conductivity increases, as shown in Figure 6a. From 22 to 500 W/(m.K), the economic thickness decreases as the thermal conductivity increases. The economic thickness has a maximum value of 39.04 cm at 22 W/(m.K). Thus, the model is able to make distinction between insulators, conductors and highly conducting materials. The insulating behavior is displayed between 0 and 22 W/(m.K), where the economic thickness increases as the thermal conductivity increases. The economic thickness adjusts its value to enhance the insulation property of a pot. Therefore, as the thermal conductivity increases, the rate of heat transfer increases. This lowers the effective heat transfer to the item in the cooking pot. Hence, the economic thickness must increase to ensure that the insulation property of the pot is enhanced. The conducting behavior is displayed between 22 to 500 W/(m.K), where the economic thickness decreases as the thermal conductivity increases and vice versa. The reason for this has been explained earlier. The high thermal conducting behavior is displayed from around 500 W/(m.K) and above, where further increase in the thermal conductivity does not lead to any significant change in the economic thickness. At this point, the metal is said to be thermally saturated. This is follows from the fact that at high temperature, the thermal conductivity of material becomes constant.
This means that the model has the ability to predict the behavior of the economic thickness of material, based on the range of thermal conductivity between which the material belongs. For example, diamonds which have been proven to have thermal conductivity as high as 2000 W/(m.K) and other materials with relatively higher thermal conductivities falls in the highly conducting category. Therefore, the economic thickness of pots made from diamond will be constant no matter the amount of dopands it might contain.
For aluminum pots whose external radius is 10 cm, the values of the economic thicknesses and cost of heating at different thermal conductivities is shown in Table 2. The highest cost of heating per year is £145.8325 at 9.00 mm economic thickness for pure aluminum pot. This is a better value than the value previously obtained by Olatona and Popoola. This is a good news for potters since they have to use little material to manufacture the 9.00 mm thickness pot. However, the users of this kind of pots spend a lot on energy when cooking with this type of pots. The lowest cost of heating, £142.2394, was obtained with pots of 101.93 mm thickness. A good news for the pots’ users, a bad news for the potters. It is therefore apparent that a balance between the cost of heating and cost of production is also essential. At constant thermal conductivity value (k=250.62 W/(m.K)), the variation of the economic thickness with outer radius of pots is shown in Figure 6b. An approximate relation connecting the economic thickness and the outer radius of the pot was also displayed. Using this relation, the radius of aluminum pots at which the economic thickness is minimum can be estimated. This is termed optimized radius. From this, an optimized size of aluminum pots can also be estimated. Hence, at this point, for pots of fixed thermal conductivity, both cost of producing the pots and cost of heating through the pots’ thickness are minimal.
| Thermal conductivity (W/(m.K)) | Economic thickness (mm) | Cost of heating (£) |
|---|---|---|
| 250.62 | 9 | 145.833 |
| 137.65 | 45.61 | 144.769 |
| 109.62 | 61.84 | 144.167 |
| 104.6 | 65.34 | 144.025 |
| 79.08 | 87.18 | 143.032 |
| 66.11 | 101.93 | 142.239 |
Table 2. Cost of heating and Economic thickness values for 10 cm radius pot at varying percentages of Lithium in the Al-Li alloys.
In summary, a model for estimating the thickness of pots at which the cost of heating through the pot’s thickness is minimized was formulated. The lowest heating cost corresponds to that of aluminum pots alloyed with 8 % by mass of Lithium, while the highest cost was recorded for aluminum pots alloyed with 0 % by mass of Lithium. Among other unique characteristics of the model are its ability to distinguish between classes of material based on the economic thickness behavior, prediction of the economic thickness of pots based on only the size of pot, prediction of the particular value of thickness and radius at which both energy and resource are most wisely spent and its applicability to pots of any shape, size and material composition. This model, if employed by potters in pots production, may scale up towards building energy, cost and resources saving kinds of pots, supporting the global aim of energy and resources management.
The authors declare that there are no conflicts of interest associated with this work.