APPM: A Narrative Data Embedding Method Using
Adaptive Pixel Pair Matching

T.Lakshmi; P.Ganga Bhavani

APPM: A Narrative Data Embedding Method Using Adaptive Pixel Pair Matching

T.Lakshmi¹,P.Ganga Bhavani²

IV year B.Tech, Dept. of CSE,Chirala Engineering College, Chirala, Prakasam(dt), Andhra Pradesh, India
Assistant professor, Chirala Engineering College, Chirala, Prakasam(dt), Andhra Pradesh, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Here we proposed a new data-hiding method based on pixel pair matching (PPM). in this paper The basic idea of PPM is to use the values of pixel pair as a reference coordinate, and coordinate search in the neighborhood used to set of this pixel pair according to a given message digit. The pixel pair is then replaced by the searched coordinate to conceal the digit.(EMD)exploitedmodificationdirection(EMD) and diamond encoding (DE) are two data-hiding methods proposed recently based on PPM. then The maximum capacity of EMD is 1.161 bpp and DE extends the payload of EMD by embedding digits in a larger notational system.this is the proposed method offers lower distortion than DE by having high compact neighborhood sets and it will also accepting embedded digits in any representative system. then it will be Compared with the (OPAP)optimal pixel adjustment process method, then this method always has lower distortion for various payloads. Experimental results reveal that the proposed method does not only provides performance better than those of OPAP and DE, but also is secure under the detection of some well-known steganalysis techniques.

Introduction

In digital image processing, while processing images here we need to follow certain criteria. Combining data into a carrier for conveying secret messages that should be confidentially is the technique of data hiding [1], [2]. After embedding, pixels of cover images will be modified and deformation occurs. The distortion caused by data embedding is called the embedding distortion [3]. A good data-hiding method must be capable of evading visual and statistical detection [4] while providing an adjustable payload [5].

Many approaches of information hiding have been proposed for diverse applications, such as patent protection, top secret transmission, tampering exposure, and figure authentication. large amount well-known data hiding format is the least significant bits (LSBs) replacement process. This process embeds fixed-length covert bits into the least significant bits of pixels by directly replacing the LSBs of cover picture with the secret message bits

Although this process is simple, it generally effects noticeable deformation when the number of embedded bits for each pixel exceeds three. Several methods have been proposed to decrease the distortion induced by LSBs replacement. Another approach of improving LSBs scheme is to decrease the amount of alterations required to be introduced into the cover image for data hiding when the numeral of secret bits is significantly less than that of available cover pixels. The method proposed by Tseng et al. [6] can cover up as many as log2(mn+1) bits of data in a binary image block sized m X n by changing, at most, two bits in the block. Matrix encoding, on the other hand, uses less than one change of the least significant bit in average to embed w bits into2w - 1cover pixels.

Diamond Encoding(DE)method is the extension of the exploiting modification direction (EMD) embedding scheme [2]. The main idea of the EMD embedding scheme is that each (2n +1)-ary notational secret digit is carried by n cover pixels, and only one pixel worth increases or decreases by 1 at most. For each block of n cover pixels, there are 2n possible states of only one pixel value plus 1 or minus 1. The 2n states of alteration plus the case in which no pixel is modified form (2n + 1) different cases. Therefore, the (2n + 1)-ary notational secret digit is embedded into the cover pixels by changing the state. Before the data embedding method, the pre-process can convert the secret data into sequences of digits with (2n + 1)- ary notational representation

II .RELATED WORK

OPAP effectively reduces the image distortion compared with the traditional LSB method. DE enhances the payload of EMD by embedding digits in a B-ary notational system. These two methods offer a high payload while preserving an acceptable stego image quality. In this section, OPAP and DE will be briefly reviewed. The OPAP method proposed by Chan et al. in 2004 greatly improved the image distortion problem resulting from LSB replacement.

A. Diamond Encoding (DE)

The EMD scheme embeds(2n + 1)-ary digit into n cover pixels, but the diamond encoding scheme can conceal (2k2 + 2k + 1)-ary digit into a cover pixel pair where k is the embedding parameter. The detail of this scheme is

described as follows.

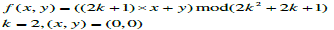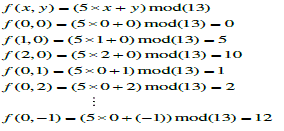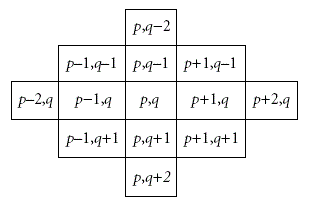
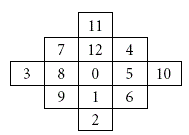
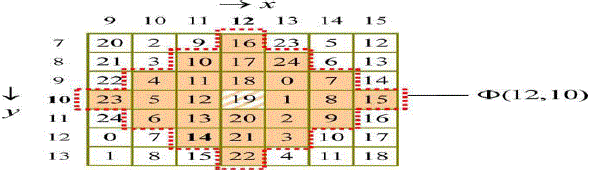
Assume that a, b, p, and q are pixel values, and k is a positive integer. The neighborhood set Sk (p, q) represents the set that contains all the vectors (a, b) with the distance to vector (p, q) smaller than k, and Sk(p, q) is defined as the above.

Let the absolute value |Sk| denote the number of elements of the set Sk, and each member in Skis called neighboring vector of (p, q). We calculate the value of |Sk| to obtain the embedding base and embedded base with a parameter k. Diamond encoding method uses a diamond function f to compute the diamond characteristic value (DCV) in embedding and extraction procedures. The DCV of two pixel values p and q can be defined as above:

where l is the absolute value of Sk. The DCV have two important properties: the DCV of the vector (p, q) is the member of Sk belongs to {0, 1, 2, . . ,l-1}and any two DCVs of vectors in Sk(p, q) are distinct. Assume that Ek represents the embedded digit and Ek belongs to{0, 1, 2, . . . ,l − 1}. For secret data embedding, we replace the DCV of the vector (p, q) with the embedded secret digit. Therefore, the modulus distance between f (p, q) and Sk is dk= f (p, q)−Ek mod l. For each k, we can design a distance pattern Dk to search which neighboring pixel owns the modulus distance dk. Then, the vector (p, q) is replaced with the neighboring vector (p’, q’) by dk. The vector (p’, q’) is the member of Sk(p, q) and the DCV of (p’, q’) equals to the embedded secret digit Ek. The vector (p’, q’) can extract the correct secret digit by above formulas The diamond encoding scheme promises that the distortion of vector (p, q) is no more than k after embedding a secret digit Ek. Therefore, this minimal distortion scheme can be employed to embed large amount of data.

III.PROCEDURE AND ALGORITHM:

A. ADAPTIVE PIXEL PAIR MATCHING (APPM)

The basic idea of the PPM-based data-hiding method is to use pixel pair (x,y) as the coordinate and thorough a coordinate(x1,y1), surrounded by a predefined locality set ?(x,y) such that f(x,y)=Sb, where f is the drawing out function and Sb, is the message digit in a -ary notational structure to be covered. Data embedding is done by replacing(x,y) with (x1,y1). For a PPM-based process, suppose a digit Sb is to be covered. The range of Sb is between 0 and B-1 , and a coordinate(x1,y1)€ ?(x,y). has to be found such that f(x1,y1)=Sb.Therefore, the range f(x,y) of must be integers between 0 and B-1, and each integer must occur at least once. In addition ,to reduce the distortion, the number of coordinates in ?(x,y) should be as small as possible.

The best PPM metbhod shall satisfy the following three requirements: 1)There are exactly B coordinates in Θ(x,y).

2)The values of extraction function in these coordinates are mutually exclusive.

3)The design of ?(x,y) and f(x,y) should be capable of embedding digits in any notational structure so that the best B can be selected to achieve junior embedding deformation.

DE is a data-hiding method based on PPM. DE greatly enhances the payload of EMD though preserving acceptable stego image quality. but, there are several problems. First, the payload of DE is determined by the selected notational structure, which is restricted by the bound ; therefore, the notational system cannot be arbitrarily selected. For example, when is 1, 2, and 3, then digits in a 5-ary, 13-ary, and 25-ary notational structure are used to surround data, respectively. However, embedding digits in a 4-ary or 16-ary (i.e., 2 bits per pixel) notational system are not supported in DE. Second, ?(x,y) in DE is defined by a diamond shape, which may lead to some unnecessary distortion when k>2 . In fact, there exists ?(x,y) a better other than diamond shape resulting in a smaller embedding deformation The wished-for method not only allows concealing digits in any notational structure, but also provides the same or even smaller embedding deformation than DE for various payloads.

B. Embedding Procedure:

Consider the cover image is of size M×M, then each of R, G, B channels will be of size M×M. S is the message bits to be concealed for each channel image and the size of S is |S|. First we calculate the minimum B such that all the message bits can be embedded. Then, message digits are sequentially concealed into pairs of pixels.

1. First minimum B satisfying |M×M / 2| ≥|SB|, and convert S into a list of digits with a B-ary notational system SB.

2. The discrete optimization problem is solved to find cB and ØB(x, y).

3. In the region defined by ØB(x, y), record the coordinate (x’, y’) such that f(x’, y’) = i, 0 ≤ i ≤ B-1.

4. Construct a nonrepeating random embedding sequence Q using a key Kr.

5. To embed a message digit sB, two pixels (x, y) in the cover image are selected according to the embedding sequence Q, and calculate the modulus distance between sB and f(x, y), then repace (x, y) with (x + x’, y + y’) [7].

6. Repeat step 5, until all the message bits are embedded To avoid any distortion because of replacing pixels right under each other in different layers, the regions Ø(x, y) for each layer are taken distinct subsets.

C. Extraction Procedure:

To extract the embedded message digits, pixel pairs are scanned in the same order as in the embedding procedure. The embedded message digits are the values of extraction function of the scanned pixel pairs.

1. The watermarked image is split into respective R, G, B layers and each is considered as a Channel Image.

2. Construct the embedding sequence Q using a key Kr.

3. Select two pixels (x’, y’) according to the embedding sequence Q.

4. Calculate f(x’, y’), the result is the embedded digit.

5. Repeat Steps 2 and 3 until all the message digits are extracted.

6. Finally, the message bits can be obtained by converting the extracted message digits into a binary bit stream.

IV.EXPERIMENTS AND EVALUTION

D. Performance

To evaluate the performance of the proposed scheme, a high definition image is taken. The simulation is run using MATLAB. First, LSB, DE, APPM and EAPPM are evaluated for Mean Square Error (MSE) with different payloads. Table 1 presents the obtained MSEs. It is observed that APPM outperforms APPM, DE and LSB.

Table2 presents the maximum payload supported by the four embedding methods at an MSE of 0.092. EAPPM is able to support 300% more than APPM. As the data is embedded in all the three layers, for EAPPM, the payload support will be more than 3 times that of APPM.

V.CONCLUSION

Proposed a simple and efficient data embedding process based on PPM. Two pixels are scanned as an embedding element and a specially designed neighbourhood set is employed to insert message digits with a smallest notational structure. APPM allows users to select digits in any notational structure for data embedding, and thus achieves a enhanced image quality. The proposed process not only resolves the low-payload trouble in EMD, but also offers smaller MSE compared with OPAP and DE. Moreover, because APPM produces no artifacts in stego images and the steganalysis results are comparable to those of the cover images, it offers a secure communication below variable embedding Capacity.

Tables at a glance


Table 1	Table 2

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4	Figure 5

References

J. Fridrich, Steganography in Digital Media: Principles, Algorithms,and Applications. Cambridge, U.K.: Cambridge Univ. Press, 2009.

N. Provos and P. Honeyman, “Hide and seek: An Introduction to steganography,”IEEE Security Privacy, vol. 3, no. 3, pp. 32–44,May/Jun. 2003.

A. Cheddad, J. Condell, K. Curran, and P. McKevitt, “Digital image steganography: Survey and analysis of current methods,”Signal Process.,vol. 90, pp. 727–752, 2010.

T. Filler, J. Judas, and J. Fridrich, “Minimizing embedding impact in steganography using trellis-coded quantization,” in Proc. SPIE, Media

Forensics and Security, 2010, vol. 7541, DOI: 10.1117/12.838002.

S. Lyu and H. Farid, “Steganalysis using higher-order image statistics,”IEEE Trans. Inf. Forensics Security, vol. 1, no. 1, pp. 111–119, Mar.2006.

Y.-C. Tseng, Y.-Y.Chen, and H.-K. Pan, “A secure data hiding scheme for binary images,” IEEE Transactions on Communications, vol. 50, no. 8, pp. 1227–1231, 2002.

W. Zhang, X. Zhang, and S. Wang, “A double layered plus-minus one data embedding scheme,”IEEE Signal Process. Lett., vol. 14, no. 11,pp. 848–851, Nov. 2007.

BIOGRAPHY

T.LAKSHMI , D/O T.CHANDRA REDDY was born in Prakasam (dist),Andhra Pradesh ,India. She is presently Studying the B.Tech (CSE) in Chirala Engineering college , Chirala affiliated to Jawaharlal Nehru Technological University, Kakinada.

P.GANGA BHAVANI was born in Prakasam(dist),Andhra Pradesh ,INDIA.She is presently working as Assistant professor at chirala engg college, Chirala affiliated to Jawaharlal Nehru Technological University, Kakinada. She is an M.tech graduate from Acharaya nagarjuna university,Guntur.She Published the research Oriented Papers in the Domain of DataWareHousing and Mining.