Keywords
|
| Kogge-Stone adder, Dadda multiplier, Brent-Kung adder, Han-Carlson adder |
INTRODUCTION
|
| High speed multiplication is a fundamental requirement in many high performance digital systems. Parallel multiplication schemes have been developed for this purpose. There are two classes of parallel multipliers, namely array multipliers and tree multipliers. Tree multipliers, also known as column compression multipliers, are known for their higher speeds making them very useful in high speed computations. Their propagation delay is proportional to the logarithm of the operand word length in comparison to array multipliers whose delay is directly proportional to operand word length [1]. Column compression multipliers are faster than array multipliers but have an irregular structure and so their design is difficult. With the improvement in VLSI design techniques and process technology, designs which were previously infeasible or too difficult to be implemented by manual layout can now be implemented through automated synthesis. |
| Two of the most well-known column compression multipliers have been presented by Wallace [3] and Dadda [4]. Both architectures are similar with the difference occurring in the procedure of reduction of the partial products and the size of the final adder. In Wallace?s scheme, the partial products are reduced as soon as possible. On the other hand, Dadda?s method does minimum reduction necessary at each level and requires the same number of levels as Wallace multiplier [5]. This paper presents a C program which generates a Verilog file for a Dadda multiplier of specified size. A comparison of post synthesis and post layout results between Dadda multiplier of varying sizes with Parallel Prefix adders in the final stage is also presented. Sections II and III explain Dadda?s algorithm and its implementation in C to create an automatic Verilog file generator. Section IV gives the post synthesis and also post layout results for the multiplier of varying sizes. |
DADDA MULTIPLIER ARCHITECTURE
|
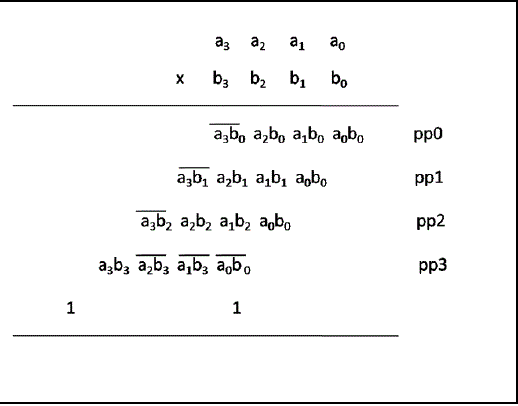
| The Dadda multiplier architecture can be divided into three stages. The first stage involves generation of partial products by two's complement parallel array multiplication algorithm presented by Baugh-Wooley [2]. In their algorithm, signs of all partial product bits are positive. It's different from conventional two's complement multiplication which generates partial product bits with negative and positive signs. The final product obtained after the reduction is also in two?s complement form. Fig.1 shows generation of partial products for 4x4 multiplier by Baugh-Wooley method. Fig. 2(a) shows the arrangement of the partial products for an 8x8 multiplier. The dots represent the partial products. |
| In the second stage, the partial product matrix is reduced to a height of two using the column compression procedure developed by Dadda. The iterative procedure for doing this is as follows: |
| 1. Let h1 = 2 and repeat hj+1 = floor (1.5*hj) for increasing values of j. Continue this until the largest j is reached, for which there exists at least one column in the present stage of the matrix with more dots than hj. Using this equation we get h1=2, h2=3, h3=4, h4=6, h5=9 and so on. e.g. in the first stage of the 8x8 Dadda multiplication shown in Fig. 2(a), the maximum height of columns is 8 therefore, the value of hj is 6 means heights of the columns are reduced to a maximum of 6. Similarly in the second stage, shown in Fig. 2(b) the maximum height of column is 6 and value of hj is 4 heights of the columns are reduced to a maximum of 4. |
| 2. All the columns, with heights greater than hj, are reduced to a height of hj using either half adder or full adder. If the column height has to be reduced by one, use a half adder else use a full adder and continue this step till the column height is reduced to hj. |
| 3. Stop the reduction if the height of the matrix becomes two, after which it can be fed to final adder. |
| Fig. 2 (b), (c), (d) and (e) show the reduction stages for an 8x8 Dadda multiplier. |
| Once the height of matrix is reduced to two, a 2N-2 bit adder is used to generate the final product. The paper describes the use of different Parallel Prefix adders for final adder stage which are described later in section III-D. |
VERILOG CODE GENERATION
|
| The main objective in writing a C program was to output a verilog file for an NxN Dadda multiplier based on the user input N. We implemented the Dadda algorithm and wrote the verilog code to a file using C to achieve this. |
A. Initialization of Verilog Modules
|
| Initially, the program prompts the user for the size of the multiplier. After accepting the size, the program creates an empty Verilog file and prints the half adder and full adder modules in it. Next it prints the gate level „and? primitive for partial product generation. After this the top-level multiplier module is printed using sub-modules generated above. |
| The top module contains two N-bit „input? data types, one 2N bit „output? data type for the multiplier, multiplicand and product bits respectively. The program also sets up N2 „wire? data type to store the partial products. Once all the above modules and data types are set up in the Verilog file, the program prints the required number of half adder and full adders to reduce column heights as explained earlier in section-II. Column reduction utilizes the dot matrix array in C, which is described below. |
B. Dot Matrix Array Creation
|
| For the purpose of implementing the column compression according to Dadda?s algorithm, the program creates an equivalent of a dot matrix array internally. The columns of the array are represented by queues (First-In-First-Out data structure). Hence the program creates 2N-1 queues, where each of the queues is implemented as a linked list. |
| The sizes and pointers to the first and last element of all queues are stored. This allows quicker enqueuing and dequeuing operations. Every element in a queue stores a string of characters, particularly the name of the wires carrying the partial product. |
| Initially, the queues are loaded with the names of the wires holding the partial products. |
C. Array Reduction
|
| Once the array, using the queues, has been created in C, it needs to be reduced according to Dadda?s algorithm. |
| The recursive procedure described in the section-II is implemented in C using a „while loop?. The size of the queues (height of columns) is reduced by using full adders and half adders. The loop stops executing when the length of all queues (height of all columns) is two or less. |
| At the start of every iteration, say iteration no. i, the sizes of all the 2N-1 queues are checked and their maximum is stored in L[i]. The value of hj is also calculated as shown in the 1st part of the iterative procedure defined in section-II. This value of hj is stored in H[i]. |
| Following the calculation of H[i], the reduction phase is initiated. The sizes of all the queues are checked sequentially starting from Queue 1. If the size of the queue is lesser than or equal to H[i], no changes are made to the queue. If the size of the queue is greater than H[i], the queue needs to be reduced to H[i] using half adders and full adders. |
| The use of either of these adders depends on the difference etween the length of the queue and H[i]. If the difference is one, half adder is used. The first two elements are dequeued and used as input to the half adder. The sum from the half adder is enqueued to the same queue and the carry out is enqueued to the next queue in sequence. For every half adder used, the size of the queue reduces by one. |
| If the difference between the length of the queue and H[i] is greater than or equal to two, full adder is used to reduce the queue. When a full adder is used, the first three elements of the queue are dequeued and are supplied as inputs to the full adder. The sum from the full adder is enqueued to the same queue while the carry out is enqueued to the next queue in sequence. For every full adder used, the size of the queue reduces by two. The above procedure is followed recursively till the size of the queue becomes equal to H[i]. After a queue is reduced, the next queue in sequence is taken up for reduction. The carries from previous queues are taken into consideration while checking the length of the queue for reduction. The iterations continue till at most two elements remain in each queue. Once such a state has been reached the „while? loop exits and the reduction phase is completed. |
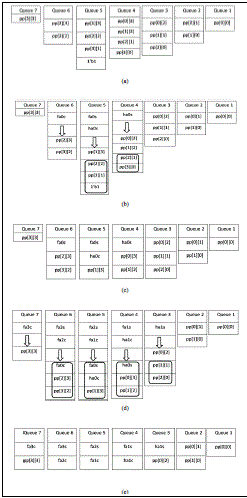
| The array reduction using queues is explained with the help of an example. A 4x4 Dadda multiplication is taken as the example. The state of the queues before the start of the reduction is shown in Fig. 3(a). The reduction of the queues for a 4x4 multiplier is explained below: |
| 1) Iteration One: On checking the sizes of all the queues, it is observed that the maximum length (L[1]) for this iteration is 4 and H[1] can be calculated to be 3. Hence all queues with sizes greater than 3 need to be reduced. Sizes of queues 1-3 are lesser than or equal to 3. Since, the length of Queue 4 is greater than the required length by 1, the first two elements of the queue are dequeued. These dequeued elements are summed in a half adder („ha0?) by printing a half adder in the Verilog file. The sum bit of the half adder is assigned to a wire „ha0s? and the carry out bit of the same half adder is assigned to the wire „ha0c?. In accordance with the algorithm, „ha0s? is enqueued to Queue 4 and „ha0c? is enqueued to Queue 5. Fig. 3(b) shows the elements to be enqueued to Queues 4 and 5. The elements above the arrow in the queue are the ones which are enqueued in this iteration. The addition of one more element to Queue 5 increased the length of the queue to 5. Hence, a full adder („fa0?) is used to reduce its length to 3. The addition of the full adder leads to dequeuing of the first three elements of Queue 5 and enqueuing of the sum of the full adder„fa0s? to Queue 5 and the carry out of the full adder „fa0c? to Queue 6. This iteration is now complete because the length of all queues is less than or equal to three. The state of the queues at the end of stage one is shown in Fig. 3(c). |
| 2) Iteration Two: On checking the sizes of all the queues, it is observed that the maximum length (L[2]) for the second iteration is 3 and H[2] can be calculated to be 2. Hence all queues with sizes greater than 2 need to be reduced. The program starts checking the sizes of the queues sequentially. Queue 3 is the first queue with length greater than 2. Since the length is only exceeded by one, a half adder („ha1?) is used to reduce the length to 2. The first two elements (enclosed by the square) are dequeued as input to half adder and „ha1s? is enqueued to Queue 3 with „ha1c? being enqueued to Queue 4. This increases the length of Queue 4 to four which is two more than the allowed size. Hence, a full adder („fa1?) is used to reduce its length to 2. The addition of the full adder leads to dequeuing of the first three elements of Queue 4 and enqueuing of the sum of the full adder„fa1s? to Queue 4 and the carry out of the full adder „fa1c? to Queue 5. This increases the size of Queue 5 to four. It undergoes the same procedure as Queue 4. Queue 6 also faces the same situation and undergoes the same procedure outlined above. Fig. 3(d) shows the elements dequeued and enqueued to Queues 3, 4, 5 and 6. The final state of the queues at the end of stage two is shown in Fig. 3(e). |
D. Final Stage Adder
|
| Once the size of all qeues has been reduced to two or less, the elements in the queues are ready to be summed using an adder. The first elements of all queues form the first input to the adder and the second elements form the second input to the adder. The size of the adder has to be 2N-2 bit for an NxN multiplier. Different Parallel Prefix adders like Kogge- Stone adder, Brent-Kung adder and Han-Carlson adder are used. The implementation of these adders is described below. |
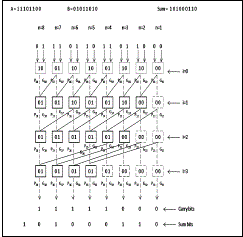
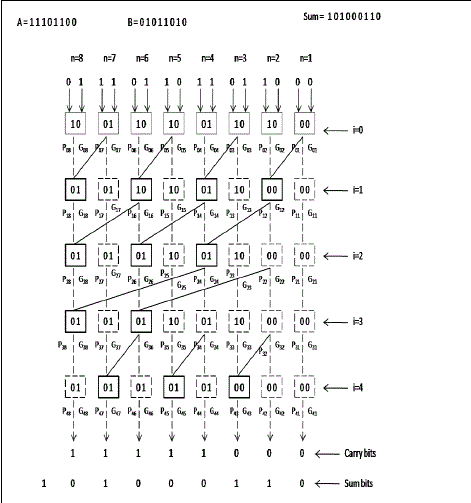
| 1) Kogge-Stone Adder: The Kogge-Stone adder generates carry signal in O(log n) time [6]. A radix-2 Kogge-Stone adder of size 2N-2 has been used as the final adder for an NxN multiplier. Fig. 4 shows the example of an 8-bit Kogge- Stone adder with no carry-in. The first bit in the boxes is the propagate bit while the second one is the generate bit. Initially (stage zero) in an N-bit Kogge-Stone adder, the propagate and generate bits are generated according to (1). |
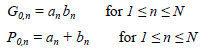 |
| where an and bn are the nth bits of the two inputs. |
| In the ith (i ≥ 1) stage the propagate and generate bits in nth block (Pi,n and Gi,n) are calculated according to (2). |
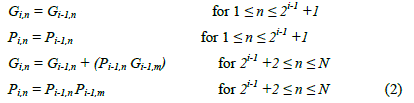 |
| where m is given by (3) |
 |
| Finally, the carry and sum bits are calculated according to (4). |
 |
| where Sn and Cn are the nth bits of the sum and carry respectively. Gf,n is the generate bit of the nth block in the final stage. |
| The numbers of stages in the adder depend upon its size. In a Kogge-Stone adder of size N, there are ceil(log2N)+1 stages. Since we need a 2N-2 bit adder for the final stage of an NxN multiplier, the number of stages in the adder are ceil[log2(2N-2)]+1. The logarithmic delay of Kogge-Stone adder is crucial in maintaining overall logarithmic delay of the multiplier. |
| 2) Brent-Kung Adder: Kogge-Stone Adder has higher performance but it takes larger area to be laid out. Brent-Kung adder can be laid out in lesser area than Kogge-Stone Adder and has lesser wiring congestion, but its time performance is poor[7]. In a Brent-Kung adder of size N, there are Ceil[2*log2(N)] stages. Initially (stage zero) in an N-bit Brent- Kung adder, the propagate and generate bits are generated according to (5). |
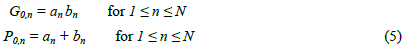 |
| where an and bn are the nth bits of the two inputs |
| In the ith (1≤ i ≤ log2(N)) stage the propagate and generate bits in nth block (Pi,n and Gi,n) are calculated according to (6). |
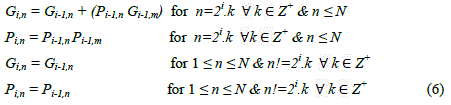 |
| where m is given by (7) |
 |
| To calculate generate and propagate bits of ith stage (log2(N)+1 ≤ i <2*log2(N)), we define three variables count, x and y. count =k where 2k is the smallest integer ≥ N and x ∈ Z+, x≥ 2 and x=2 for i= log2(N)+1 and is incremented by 1 for every subsequent stage and |
 |
| Now in the ith stage the propagate and generate bits in nth block (Pi,n and Gi,n) are calculated according to |
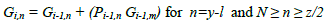 |
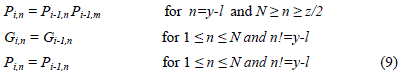 |
| where m and l are given by (10) and (11) respectively |
 |
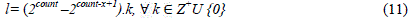 |
| Finally, the carry and sum bits are calculated according to (12). |
 |
| where Sn and Cn are the nth bits of the sum and carry respectively. Gf,n is the generate bit of the nth block in the final stage. |
| Fig. 5 shows the example of an 8 bit Brent-Kung Adder. Since we need a 2N-2 bit adder for the final stage of an NxN multiplier, the number of stages in the adder are ceil[2*log2(2N-2)]. |
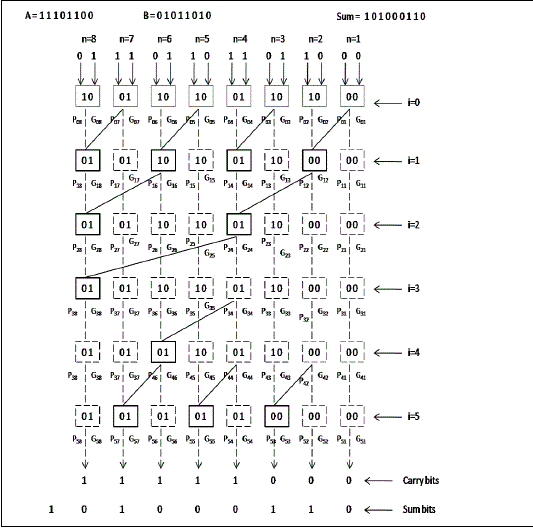
| 3) Han-Carlson Adder: Brent-Kung adder reduces area and power but do not produce minimum depth parallel prefix circuits. Their delay time is also high (2*log2N – 1). Kogge-Stone adder has lesser delay (log2N) but it has high area and power. By combining B-K & K-S graphs, Han and Carlson obtained a new hybrid prefix graph that achieves intermediate values of area and time[8]. An example of 8 bit Han-Carlson Adder is shown in Fig. 6. The numbers of stages in the adder depend upon its size. In a Han-Carlson adder of size N, there are Ceil[log2(N)+2] stages. |
| Initially (stage zero) in an N-bit Han-Carlson adder, the propagate and generate bits are generated according to (13 |
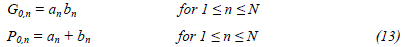 |
| where an and bn are the nth bits of the two inputs |
| In the ith (1≤ i ≤ log2i,n and Gi,n) are calculated according to (14) |
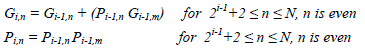 |
| Let S={n?2i-1+2 ≤ n ≤ N, n is even} |
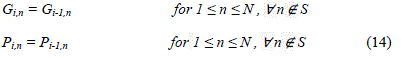 |
| where m =n – 2i-1 |
| In the last stage(i=log2(N)+1) the propagate and generate bits in nth block (Pi,n and Gi,n) are calculated according to (16 |
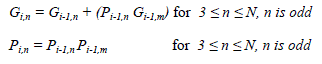 |
| Let R={n?3 ≤ n ≤ N, n is odd} |
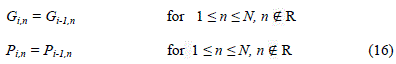 |
| Finally, the carry and sum bits are calculated according to (17). |
 |
| where Sn and Cn are the nth bits of the sum and carry respectively. Gf,n is the generate bit of the nth block in the final stage. |
| Since we need a 2N-2 bit adder for the final stage of an NxN multiplier, the number of stages in the adder is given by ceil[log2(2N-2)+2]. |
RESULTS AND DISCUSSION
|
| All the multiplier designs use Verilog as the HDL. The synthesis and post layout results of Dadda multiplier with all the parallel prefix adders discussed in the previous section were compared. This section provides the delay in millisecond, area in square micrometer and power in milliwatt for all the architectures mentioned above. The synthesis was performed in Cadence RTL Compiler using 90 nm UMC technology libraries at typical (tt) conditions. The synthesized netlist was used along with design constraint .sdc file, technology library file and .lef files for generating the layout using SOC Encounter tool. The layouts have been done for Dadda multiplier of different sizes and their post layout results have been tabulated. The post layout results follow the same trend as the post synthesis results. |
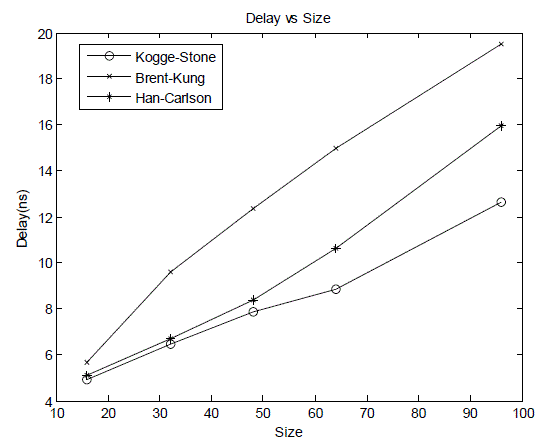
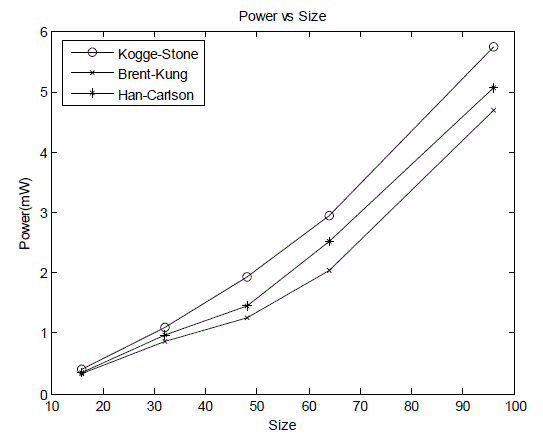
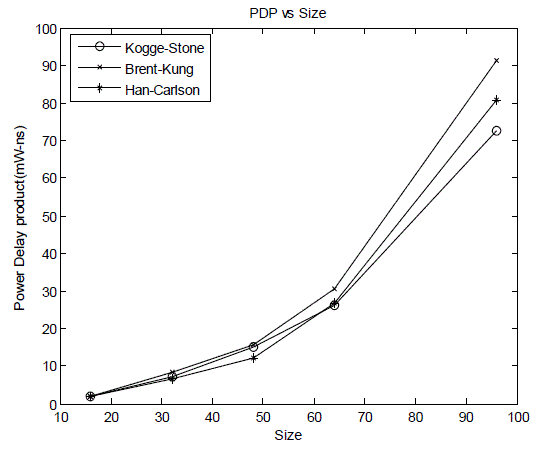
| The post layout area is the area of core which includes area of standarad cells as well as the area of interconnect wires. Fig.7 shows that the multiplier with Kogge-Stone adder in the final stage is much faster than with all other adders but it?s power consumption is the highest of all as shown in Fig. 8. Fig.9 compares the Power Delay Products |
| It can be observed that Dadda multiplier with Kogge-Stone and Han-Carlson adders in the final stage has lower Power Delay Products than with Brent-Kung adder. Dadda multiplier with Brent-Kung adder gives lower power and area when compared to that with Kogge-Stone and Han-Carlson adders but owing to the higher delay, their Power Delay Product is also higher. |
CONCLUSION
|
| This paper explains an easy and efficient method of generating synthesizable Verilog code for Dadda multipliers of user specified size. It also shows that the use of Parallel Prefix adders in the final stage greatly improves the speed of Dadda multiplier and also gives lower Power Delay Products. The logarithmic delay of the Parallel Prefix adders supplements the logarithmic delay of the compression tree to provide an overall logarithmic delay. |
Tables at a glance
|
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
|
| |
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
|
| |
References
|
- P. R. Cappello and K Steiglitz, “A VLSI layout for a pipe-lined Dadda multiplier,” ACM Transactions on Computer Systems 1,2(May 1983) , pp. 157-17
- Baugh, Charles R.; Wooley, B.A., "A Two's Complement Parallel Array Multiplication Algorithm," Computers, IEEE Transactions on , vol.C- 22, no.12, pp.1045,1047, Dec. 1973
- Wallace, C. S., "A Suggestion for a Fast Multiplier," Electronic Computers, IEEE Transactions on , vol.EC-13, no.1, pp.14,17, Feb. 1964
- L. Dadda, “Some schemes for parallel multipliers,” Alta Frequenza, vol. 34, pp. 349–356, 1965
- Townsend, W. Swartzlander, E. Abraham, J., "A Comparison of Dadda and Wallace Multiplier Delays". SPIE Advanced Signal Processing Algorithms, Architectures, and Implementations XIII.
- Kogge, Peter M.; Stone, Harold S., "A Parallel Algorithm for the Efficient Solution of a General Class of Recurrence Equations," Computers, IEEE Transactions on , vol.C-22, no.8, pp.786,793, Aug. 1973
- Brent, Richard P.; Kung, H. T., "A Regular Layout for Parallel Adders," Computers, IEEE Transactions on , vol.C-31, no.3, pp.260,264, March 1982
- Han, Tackdon; Carlson, D.A., "Fast area-efficient VLSI adders," Computer Arithmetic (ARITH), 1987 IEEE 8th Symposium on , vol., no., pp.49,56, 18-21 May 1987
|