Axiomatic Proof of the Properties of the Complex Plane through Constants

Abstract

Generalisis of the fundamentality of mathematical constants, and their application on the complex Cartesian coordinate system, as an analytical framework to ascertain their relation, and that, which they retain with respect to the mechanisms of a circle.

Keywords

Fundamentality; Mathematical constants; Analytical framework

Introduction

The dimensionality of space given time does not depend on the techniques deployed to analyse it. But has its generality on the context that it is universal, and a simple subject of the complex plane. Euler’s identity and the golden ratio: Tends to factor well into the equation of pi that they are its approximate value at a certain interval [1]. To understand this behaviour, is to have thorough apprehension of the entire existence of the coordinate system. Once space is defined as a set of coordinates. Then, the spatiality of each dimension is defined appropriately, by its relation to other dimensions. Therefore space is not just the imagination of the brain. But the force that is the fundamental nature of the universe [2].

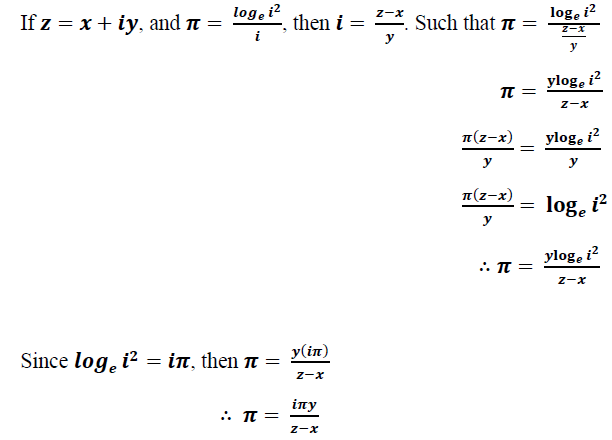
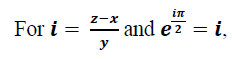
then it follows arguably, that the unit circle has a diameter of a closed interval not greater than two.

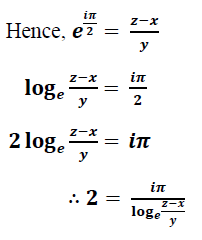
And given that

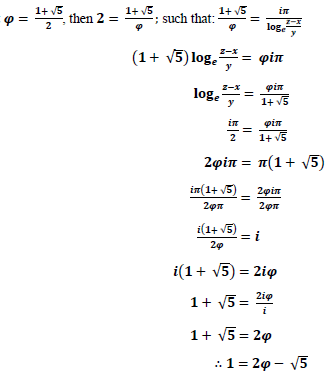
If there exist no any other number than π that defines a circle so well; then such a constant must prove to be more fundamental than it is known. Or if functions relate: it is not only as one to one functions that they are proven to exist. If such functions can be approximated to any fundamental constant known. That validates their existence, and mostly, justifies the complexity of their nature in space [3].

Thus, it cannot be other than true that the following holds:

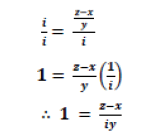
So that it also holds as follows:

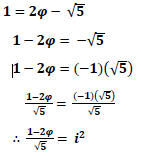
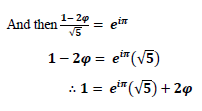
Which suggests the following as the approximate value of Euler’s identity: given its relation to

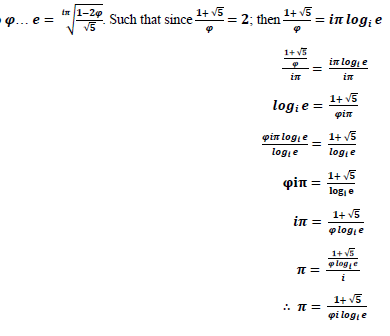
And thus;

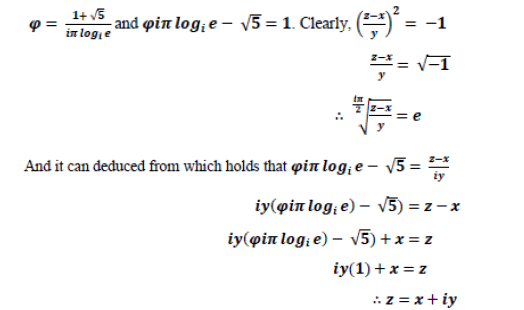
And from x²+y²=1 and its extension on the plane; gives rise to the multidimensionality of space as relative to how the mechanisms of coordinates affects each other on the Cartesian coordinate system [4]. Anything through it, should hold even everything which cannot be stated otherwise, or said proven not to exist [5,6]. Hence, what follows applies:

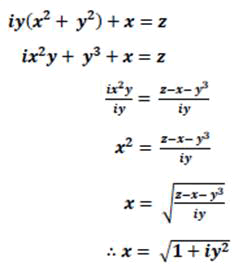
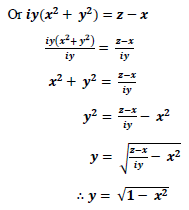
So that it is true that

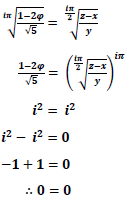
Which then translates

CONCLUSION

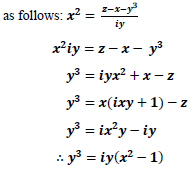
While generalisation on the spatial concept of time means that space is simply complex. It is easier to see the world in singular form, rather than through a unified concept. Hence, mostly, it is easier for relative phenomena to be conceptualised as separate quantities, such as zero or one. However, the world of space is not limited to any quantities. A self-sufficient object would encompass anything, or have the capacity of being everything. And the only limit to it would be its validity, and truth. When it can be false because of misapplication; not because it is not covariant. Then that is as fundamental, as any constant, in the mathematics of the universe. For it is known now, that black holes in mathematics are mathematical constants that connects dimensions. And any self-sufficient system can be able to regenerate itself in the process.

References

1. Gibson CG, et al. Elementary Euclidean Geometry: An introduction. Cambridge University Press, United Kingdom. 2003.
2. Ultrich L, et al. Introduction to differential Calculus: Systematic studies with Engineering Applications for Beginners. New Jersey. 2012.

   [Google Scholar]

3. Andreescu T, et al. Complex numbers from A to…Z. Springer, Birkhauser, New York. 2005; 318.

   [Google Scholar]

4. Rugh HH, et al. Generalized Fredholm determinants and Selberg zeta functions for Axiom a dynamical systems. Ergod Theory Dyn Syst. 1996;16:805-819.

   [Crossref] [Google Scholar]

5. Beurling A, et al. Dirichlet spaces. Proc Natl Acad Sci USA. 1959;45:208-215.

   [Crossref] [Google Scholar] [PubMed]

6. Betancor JJ, et al. Axiomatic Potential Theory, Asymptotic Values and Elliptic Differential Operators. Potential Anal. 2000;2:115-146.

   [Crossref] [Google Scholar]