ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Lakshmi Pratyusha P1, Shanmukha Priya V2, VPS Naidu3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Condition Monitoring is one of the most important techniques for maintenance of a machine. This is done in order to increase the safety and reliability of the machine. There are several types of condition monitoring for aircraft engine bearing health monitoring such as, Oil Debris Monitoring, Temperature Monitoring, and Vibration Monitoring. Among these, vibration monitoring is found to be the most widely used technique. The current work focuses on the Time Domain Analysis in Vibration Monitoring of a rolling element bearing. This type of analysis depends on several statistical features which are used to identify the defects in the bearing. The extraction of these features is done by a method called feature extraction. It involves calculating features using the raw vibration data and also finding the features using time derivative and time integral of the vibration data. In addition to that, a Graphical User Interface (GUI) has been designed which enables the user to give input data and obtain the fault analysis and plots of time domain analysis.
Keywords |
||||||||||
| Condition Monitoring, Time domain analysis, Vibration analysis, Graphical User Interface (GUI) | ||||||||||
INTRODUCTION |
||||||||||
| Condition monitoring is the process, which monitors the engine parameters periodically in order to ensure safety of the machine and hence predicts the faults in the system before a catastrophic failure occurs [1]. Condition monitoring mainly consists of two stages, which are, diagnosis and prognosis. Diagnosis is the process in which the data is collected and analysed in order to find the faults of the machine (in this case, bearing). Prognosis is the process in which the remaining useful life (RUL) of the bearing is predicted using the data from diagnosis [2]. The current work focuses only on part of the diagnosis stage of condition monitoring for aircraft engine bearing health monitoring. | ||||||||||
| Bearings are critical components in rotating machinery. Bearings which transfer loads via a rolling element are called as rolling element bearings. Ball bearing is a type of rolling element bearing, which is used in the present work. There are four main components in a bearing, namely, inner ring or inner race, outer ring or outer race, rolling elements and a cage or separator. It is to be noted that, the faults occur in any one of the above-mentioned components. The elements of a rolling element bearing are shown in Fig-1. | ||||||||||
| In Fig-1, the inner race is the rotating part, whereas outer race is the stationary part. Rolling elements roll in between the inner and outer race, and transfer the loads. Cages or separators are used to separate the rolling elements in order to prevent friction between them [3]. | ||||||||||
| Vibration Monitoring is employed here as a method for monitoring the condition of the bearing. This is done by the use of accelerometer, which senses the vibration in the bearing and provides the required data for analysis. Vibration monitoring is carried out using any of the three methods, namely, Time domain analysis, Frequency domain analysis, and Time frequency analysis. All the three techniques have been described in detail in [4]. Among the three techniques, time domain analysis is the simplest and easy to implement. It requires the calculation of statistical features, using which the faults can be classified. Frequency domain analysis is one in which the characteristic defect frequencies of a bearing can be found out, which provide information on the type of bearing fault. This analysis is carried out by Fast Fourier Transform, Hilbert Transform, etc. Time frequency analysis provides both time and frequency information which makes it the most useful method of all. Time frequency analysis can be implemented using Wavelet Transform, Short Time Fourier Transform and Wigner-Ville distribution [5]. In this paper only time domain analysis of bearing vibration data has been presented. | ||||||||||
TIME DOMAIN ANALYSIS |
||||||||||
| Time domain analysis is the process in which statistical features are computed from the vibration data. By comparing the statistical features, particular faults can be identified. The statistical features that are used for time domain analysis in the present work are mean (μ), variance (σ2), Root Mean Square (RMS), Kurtosis (Kt), Skewness (Sn), and normalized central moments (c5 to c8). These statistical features are described in this section. | ||||||||||
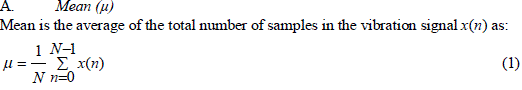 |
||||||||||
| where, N is the length of the vibration signal | ||||||||||
| x(n) is the raw vibration signal | ||||||||||
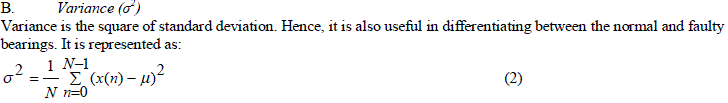 |
||||||||||
| C. Root Mean Square (RMS) | ||||||||||
| The Root Mean Square (RMS) value indicates the power content in the vibration signal. RMS is the effective value of the vibration signal. It can also be defined as the standard deviation of the signal. It is a feature, suited for steady state signals. As the bearing life approaches the end RMS level increases considerably [6]. It provides excellent results in following the noise level throughout the signal and is the normalized second statistical moment of the signal [7]. It is represented as: | ||||||||||
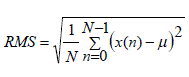 (3) (3) |
||||||||||
| D. Skewness (Sn) | ||||||||||
| Skewness is the normalized third statistical moment of the signal. It indicates the relative energy over and under the mean level [8]. It is represented as: | ||||||||||
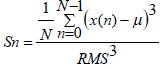 (4) (4) |
||||||||||
| E. Kurtosis (Kt) | ||||||||||
| Kurtosis is the normalized fourth statistical moment of the signal. It indicates the impulsive nature of the signal. Since the signal is raised to the fourth power, it effectively amplifies the isolated peaks in the signal [9]. Kurtosis value is a negotiation between the tactless lower moments and extra-sensitive higher moments [8]. Kurtosis increases rapidly at the initial stage of a fault itself which is very helpful in finding the faults [6]. For continuous time signals, kurtosis is defined as: | ||||||||||
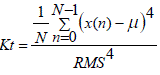 (5) (5) |
||||||||||
| F. Normalized central moments (c5 to c8) | ||||||||||
| Three of the normalized central moments have been discussed above (RMS, Skewness, and Kurtosis). Similarly, the higher order moments from normalized fifth central moment (c5) to normalized eighth central moment (c8) can be found by raising the power in the expression correspondingly. They are represented by equations (6) to (9). | ||||||||||
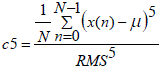 (6) (6) |
||||||||||
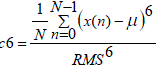 (7) (7) |
||||||||||
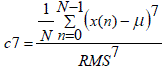 (8) (8) |
||||||||||
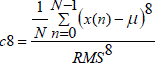 (9) (9) |
||||||||||
SIGNAL PRE-PROCESSING |
||||||||||
| In this paper, raw vibration signal (the original signal directly sensed by accelerometer during the experiment), time derivative of the raw vibration signal and time integral of the raw vibration signal are considered. Using the raw vibration signal, the nine features defined in the previous section are calculated. Similarly, eighteen features can be calculated using the time derivative and time integral of the vibration data. The time derivative and time integral of the vibration signal are calculated as [10]: | ||||||||||
| where, n is the sample number (index) | ||||||||||
| dx(n) is the time derivative of the raw vibration signal x(n) | ||||||||||
| ix(n) is the time integral of the raw vibration signal x(n) | ||||||||||
RESULTS AND DISCUSSION |
||||||||||
| Feature extraction techniques are applied on an open source bearing data. The bearing data have been obtained from the bearing test rig of ‘The Case Western Reserve University’ [11]. The bearing used here is 6205-2RS JEM SKF, deep groove ball bearing. The experimental test stand used to collect data consists of a 2 hp motor, a torque transducer, dynamometer and control electronics. Single point faults were introduced to the test bearing using electro-discharge machining and the vibration data was collected using the accelerometers attached to the housing of the setup. Vibration signals were collected using a 16 channel DAT recorder and post processed using MATLAB and the resulting data were stored in MAT files. The dimensions of the bearing used here are: | ||||||||||
| Number of balls NB = 9, | ||||||||||
| Ball diameter DB = 0.3126 inches, | ||||||||||
| Pitch diameter C | ||||||||||
| Contact angle of the bearing ïÃÂñ = 0 degrees. | ||||||||||
| The raw vibration signal, time derivative and time integral of the vibration signal for the normal bearing are illustrated in Fig-2. In the current work, the vibration data were divided into 25 segments, consisting of 2048 samples each as shown in Fig-2. Then, nine features have been obtained keeping the raw signal as it is, and 18 features were obtained taking the time derivative and time integral of the raw vibration signal. The mean ± standard deviation values of all the features of time domain analysis are given in Table I. In this paper, the bearing defects such as inner race defect (IRD), outer race defect (ORD) and ball defect (BD) are considered. | ||||||||||
| From Table I, it can be observed that the mean ± standard deviation values of normal bearings are lesser compared to the faulty bearings. For the features variance and Root mean square, the mean ± standard deviation values follow the trend and hence the values are small for normal bearings and large for the defective bearings. Hence, it is obvious that, these 6 features (in raw signal, time derivative and time integral) provide better results in differentiating between the normal and faulty bearings. For all the remaining features, it is not the case, as the values for normal and ball defect bearings are approximately same, and hence it is not possible to differentiate the faulty bearings from the normal one. The average values of all the statistical features were plotted. Few of the plots in which the features were clear for fault classification are described in this section. The plot of average Variance from all the segments is shown in Fig-3. From Fig-3, it is clear that, The feature variance clearly separates the normal bearing from the faulty bearings in all three conditions and also separates among inner, ball, and outer race defective bearings and this feature may be useful in fault classification. The plot of Root Mean Square (RMS) versus segments is shown in Fig-4. From Fig-4, the plot of normal bearings is isolated from that of faulty bearings in all conditions distinctly similar to the previous case in all three conditions and also differentiates among the faulty bearings. Hence, RMS is also a very useful feature in fault classification. The plots of remaining features did not give clear information on fault classification and are overlapping with each other. Hence their plots are not included here. The features useful for fault classification are shown in Table II. | ||||||||||
GRAPHICAL USER INTERFACE (GUI) |
||||||||||
| A Graphical User Interface (GUI) has been created using Graphical User Interface Design Environment (GUIDE) in MATLAB. The created GUI is shown in Fig-5. | ||||||||||
| In Fig-5, using the list box ‘Choose File’, the user has to select the required file. The drive end data of the selected file is loaded in list box ‘Data – DE’. Then, the type of signal has to be selected by the user, such as raw signal, time derivative, or time integral. The features are displayed in the drop down box ‘select feature’. Any one of the feature can be selected, so that, the selected feature will be plotted against the number of segments into which the vibration signal is divided (in this case, 25). In addition to that, the mean ± standard deviation values of the selected feature are displayed in the message box. | ||||||||||
| Then, using these values, the fault can be classified. Hence, when the ‘type of fault’ button is pressed, the type of fault is displayed based on the values of mean ± standard deviation of the feature ‘RMS’. This feature is chosen since it gives better results than the remaining features as shown in Fig-4. Pressing the exit button closes the GUI. When the export button is pressed, the whole GUI window is exported to a new word document and the document will be opened. | ||||||||||
CONCLUSION |
||||||||||
| This paper presents a review on the time domain analysis technique for the condition monitoring of the bearing. The time domain analysis was implemented on the bearing data obtained from the open source (data generated at bearing test facility at The Case Western Reserve University) and statistical features of the data were extracted to classify the bearings defect.. As a result of feature extraction, the features which are useful for fault classification have been determined. Those features are variance and Root mean square. This has been established by calculating the mean ± standard deviation values of all the features, as these values vary largely, thus showing the differentiation between the normal and defective bearings. The plots also showed a clear distinction among normal bearing, inner race defective bearing, ball defective bearing and outer race defective bearing. This feature extraction can be used in future in that, these features can be fed as input for training the neural networks or for the support vector machines (SVM) in order to carry out fault classification. A Graphical User Interface (GUI) was also designed which produces results and plots when the input data is selected by the user. | ||||||||||
Tables at a glance |
||||||||||
|
||||||||||
Figures at a glance |
||||||||||
|
||||||||||
References |
||||||||||
|