ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Shanmukha Priya V1, M.R. Ramesh1, VPS Naidu2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Condition monitoring is used to frequently monitor the parts of an engine. Since the failures are predicted in advance, the lifetime of the machine is increased, thereby minimizing the maintenance costs. Among the many techniques used for condition monitoring such as static, dynamics, thermal and Tribology, vibration analysis comes under the dynamic techniques. In this paper, the frequency domain analysis, which is one of the commonly used techniques in vibration analysis, is used for diagnosis of bearing faults. The methods used for frequency domain analysis in this paper are Discrete Fourier Transform (DFT), Envelope Analysis and Resampling. It has been found out that, envelope analysis gives better results than the remaining methods.
Keywords |
||||||||||||||
| Bearing health diagnosis, Frequency domain analysis, Envelope Analysis, Resampling | ||||||||||||||
INTRODUCTION |
||||||||||||||
| Integrated Vehicle Health Monitoring (IVHM) is one of the emerging trends in health monitoring. IVHM is the process in which data is collected in real time using sensors and continuous monitoring is done. This is called as conditionbased maintenance [1]. IVHM involves structural health monitoring, landing gear monitoring, engine bearing health monitoring, etc and combines everything in order to predict the complete performance of the vehicle. The percentage of the bearing faults in a engine is 42%, which is more compared to the other faults [2]. Hence bearing health condition monitoring is one of the major areas of condition monitoring. Bearings are used to connect the rotating parts of an engine in order to run the engine. The fundamental elements of a bearing are inner race, outer race, cage and rolling elements, i.e. balls [3]. For performing the frequency domain analysis, characteristic defect frequencies have to be found out. The characteristic defect frequencies of the bearing are calculated based on the bearing dimensions such as number of balls in the bearing ( NB ), pitch diameter ( DC ), ball diameter ( DB ), contact angle ( ), and shaft frequency ( FS ). These dimensions, along with the bearing elements are illustrated in Fig-1. | ||||||||||||||
CHARACTERISTIC DEFECT FREQUENCIES |
||||||||||||||
| There are five types of characteristic defect frequencies in a bearing. The units of these frequencies are Hz and these can be calculated based on the following formulae [3]: | ||||||||||||||
| A. Shaft Rotational Frequency ( FS ) | ||||||||||||||
| For the movement of bearings, shafts are important and hence the shaft rotational frequency is also an important factor. Based on this frequency only, other frequencies can be calculated. The shaft rotational frequency is represented as: | ||||||||||||||
| where, RPM is the rotational speed in revolution per minute | ||||||||||||||
| B. Outer Race Defect Frequency ( FBPO ) | ||||||||||||||
| The rate at which the balls pass a point on the path of outer race is given by outer race defect frequency. This is the most important frequency as this gives better results than the others, since outer race is the one where accelerometer is fixed to monitor the bearing. It is computed as: | ||||||||||||||
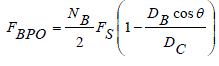 (2) (2) |
||||||||||||||
| where, NB is the number of balls in the bearing | ||||||||||||||
| DB is the ball diameter | ||||||||||||||
| DC is the pitch diameter of the bearing | ||||||||||||||
| is the contact angle of the bearing | ||||||||||||||
| C. Inner Race Defect Frequency ( FBPI ) | ||||||||||||||
| The rate at which the balls pass a point on the path of inner race is given by inner race defect frequency. It is represented by the equation: | ||||||||||||||
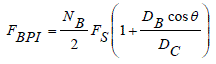 (3) (3) |
||||||||||||||
| D. Fundamental Cage Frequency ( FC ) | ||||||||||||||
| The rotational frequency of the cage is called fundamental cage frequency. The cage avoids the rubbing of balls against each other in order to reduce wear and friction. It is also called as fundamental train frequency and is represented as: | ||||||||||||||
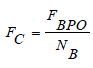 (4) (4) |
||||||||||||||
| E. Ball Spin Frequency ( FB ) | ||||||||||||||
| The rate at which the balls rotate its own axis is called ball spin frequency. It is represented by the equation: | ||||||||||||||
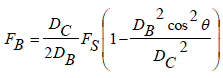 (5) (5) |
||||||||||||||
METHODS IN FREQUENCY DOMAIN ANALYSIS |
||||||||||||||
| The frequency domain analysis involves analysing bearing vibration data based on the frequency. Methods which are used for this analysis are: | ||||||||||||||
| ïÃâ÷ Discrete Fourier Transform (DFT) | ||||||||||||||
| ïÃâ÷ Envelope Analysis | ||||||||||||||
| ïÃâ÷ Resampling | ||||||||||||||
| A. Discrete Fourier Transform (DFT) | ||||||||||||||
| Most of the bearing vibrations are periodical in nature and hence it is easy to extract the features using DFT. The DFT converts the time domain signal into frequency domain. This is done by splitting the time domain data into several segments and DFT is applied on each segment. The discrete Fourier transform of a signal x(n) of length N can be mathematically defined as: | ||||||||||||||
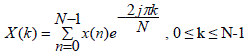 (6) (6) |
||||||||||||||
| In DFT, the characteristic defect frequencies are given by peaks in the frequency spectrum, which helps to identify the difference between the normal and faulty bearings. Here, many peaks are masked by noise, which is the limitation of FFT. Envelope Analysis overcomes this limitation. FFT is calculated in MATLAB using the function 'fft'. A part of the code used for FFT analysis is given below: | ||||||||||||||
| T=length(x)/Fs; % time interval [X,F] = positiveFFT(x,Fs); X(1)=X(2); Nt = round(1600*T); fq = F(1:Nt)'; XS = abs(X(1:Nt));XS(1)=XS(2); | ||||||||||||||
| function [X,freq] = positiveFFT(x,Fs) N = length(x); % get the number of points k = 0:N-1; % create a vector from 0 to N-1 T = N/Fs; % get the time interval freq = k/T; % create the frequency range X = fft(x)/N; % make up for the lack of 1/N in Matlab FFT cutOff = ceil(N/2); % taking only the first half of the spectrum X = X(1:cutOff); freq = freq(1:cutOff); | ||||||||||||||
| B. Envelope Analysis | ||||||||||||||
| Envelope analysis is used to extract the characteristic defect frequencies of the bearing [5]. In order to overcome the noises which were obtained in FFT spectrum, demodulation is done here. The important step in amplitude demodulation is the rectification of the signal. This is carried out to isolate the frequencies with the help of Hilbert transform. Envelope analysis consists of finding the magnitude of analytical signal and taking its FFT [6]. The analytical signal consists of real part and imaginary part, of which the imaginary part is the Hilbert transform. Let the analytical signal xa (t) be given by, | ||||||||||||||
| Here, the real part x(t) is the vibration signal. The imaginary part is Hilbert transform of x(t) and is given by the equation, | ||||||||||||||
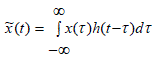 (8) (8) |
||||||||||||||
| The magnitude of the analytical signal is: | ||||||||||||||
| The analytical signal is in time domain. By taking FFT of the analytical signal, it is converted into frequency domain and then envelope analysis is obtained. For carrying out envelope analysis in MATLAB, the Hilbert transform is first calculated using the function 'hilbert' and then applying FFT using the same code used for FFT as described in section- A. | ||||||||||||||
| C. Resampling | ||||||||||||||
| Resampling is used for sample rate conversion. This is carried out by means of two steps namely, interpolation and decimation [7]. The sample rate of the vibration signal is increased in the process of interpolation and decreased in the process of decimation. Resampling is done to obtain the low frequency band. The operation of resampling is explained through Fig-2. | ||||||||||||||
| In Fig-2, x(n) is the input vibration signal. Interpolation is carried out on the signal by a factor of P and then it is passing through a filter to prevent aliasing. After that, decimation is carried out on the filtered signal by a factor Q and the resultant signal is the resampled signal y(n). By using this process, desired sample rate of a signal can be obtained. The resampling is carried out in MATLAB using the command ‘resample’. Here, P is taken as the required sample rate and Q as the original sample rate. By performing the Envelope analysis over the resampled signal gives the resampled spectrum. | ||||||||||||||
RESULTS AND DISCUSSIONS |
||||||||||||||
| The above three frequency domain analysis have been carried out in MATLAB on the open source bearing data obtained from the bearing test rig of Case Western Reserve University [8]. The bearing used was 6205-2RS JEM SKF, deep groove ball bearing. The components used for the experiment are 2 hp motor, a torque transducer, and dynamometer. The details of the test conducted can be found in [8]. After analysing the vibration signals in MATLAB, the results obtained are plotted and comparison is done. The dimensions of the bearing used are: | ||||||||||||||
| Number of balls NB = 9, | ||||||||||||||
| Ball diameter DB = 0.3126 inches, | ||||||||||||||
| Pitch diameter D = 1.537 inches, | ||||||||||||||
| Contact angle of the bearing = 0 degrees. | ||||||||||||||
| The characteristic defect frequencies calculated for the vibration data for different RPMs have been tabulated in Table | ||||||||||||||
| From Table I, it can be observed that, as the RPM decreases, there is decrease in the characteristic defect frequencies. These form the basis for all the three frequency domain methods. Mathematical relation between the RPM and the characteristic defect frequencies have been done using curve fitting tool available from MATLAB. We consider first order linear equation to fit the data. Let RPM be an x and FBPO be a y, then the unknown m and c (as in eq. 10) are found by fitting the data using curve fitting tool. The relationship between the RPM and FBPO is shown in Fig-3. It can be observed that, there is a linear relationship between the two parameters, which follows the straight line equation (10): | ||||||||||||||
| Similar results are obtained when RPM is plotted against the remaining frequencies such as inner race defect frequency, ball spin frequency, shaft frequency and cage frequency. There are certain parameters which provide the goodness of fit. These are called goodness of fit statistics [9], which are:q | ||||||||||||||
| ïÃâ÷ Sum Squares Error (SSE) | ||||||||||||||
| ïÃâ÷ R square | ||||||||||||||
| ïÃâ÷ Root Mean Square Error (RMSE) | ||||||||||||||
| The sum of squares due to error (SSE) measures the deviation of the given values from the fit. SSE value has to be closer to 0 in order to get a better fit. The R square value measures success in the variation of data [9]. The value should be between 0 and 1 for a better fit. Root Mean Square Error (RMSE) denotes the index to the goodness of fitting. A smaller RMSE value represents a good fitting [10]. | ||||||||||||||
| The goodness of fit statistical parameters for all the five characteristic defect frequencies with respect to RPM is shown in Table- II. From Table II, it can be seen that, the values of SSE are close to 0, R-square close to 1, and RMSE values are small indicating that all the three parameters satisfy the conditions for a better fit. The coefficients 'm' and 'c' are those which relate the RPM and characteristic defect frequencies as shown in equation (10). The harmonics of these characteristic defect frequencies are calculated and tabulated in Table III. | ||||||||||||||
| From Table III, it can be noticed that the harmonic spacing is obtained in the plots in an interval of the values mentioned in the above table. In Table III, shaft frequency and cage frequency are dominant in all the cases and hence the harmonics of those frequencies appear in almost all the cases. The remaining three frequencies, which are, inner race defect frequency, outer race defect frequency, ball spin frequency and their harmonics are specific to the particular bearings in which the respective faults occur. The magnitudes corresponding to the harmonics of outer race defect frequency in the frequency spectrum for different types of bearing defects are given in Table IV. | ||||||||||||||
| In Table IV, OF1 to OF8 indicate the harmonics of outer race defect frequency. It is observed from the table that the magnitudes corresponding to the harmonics of outer race defect frequency for the outer race defective bearings are very high compared to other defects. Thus, outer race defect frequency is a useful feature in finding that the bearing has an outer race defect. Table V shows the values of magnitude in the frequency spectrum for the harmonics of inner race defect frequency. | ||||||||||||||
| In Table V, IF1 to IF8 represent the harmonics of inner race defect frequency. It can be observed from the table that the values of magnitudes corresponding to the harmonics of inner race defect frequency for the inner race defective bearings are very high compared to other defects. Hence, inner race defect frequency is a useful feature in finding that the bearing has an inner race defect. Table VI shows the magnitudes corresponding to the harmonics of ball spin frequency. | ||||||||||||||
| In Table VI, BF1 to BF8 indicate the harmonics of ball spin frequency. From table, it can be seen that, for the third (BF3), fifth (BF5) and sixth (BF6) harmonics, the values of magnitude are distinct from the remaining defects. Hence, this feature is useful for the identification of the ball defect in the bearing. Since the ball hits both the inner and outer raceway, it is modulated by both the inner and outer race defect frequencies. Hence, it can be observed that, the magnitudes are also somewhat higher for the inner and outer race defective bearings than the remaining cases. The comparison of three methods in frequency domain analysis for the inner race faulty bearings is shown in Fig-4. | ||||||||||||||
| From Fig-4 it can be observed that, many of the peaks are masked by noises in FFT analysis. In envelope analysis, the peaks of characteristic defect frequencies are clear till the eighth harmonics. Here, the inner race defect frequency decreases from higher value to lower value till fourth harmonics and then increases suddenly in the fifth harmonics and the same trend continues after that. Resampling shows the lower order frequency range clearly. Hence, for this case, resampling can be concluded as a better method. Fig-5 shows the comparison of frequency domain methods for outer race faulty bearings. | ||||||||||||||
| In Fig-6, FC represents the cage frequency, FBPO represents the outer race defect frequency and FBPI represents the inner race defect frequency. From Fig-6, it can be inferred that, harmonics of ball spin frequency cannot be identified by any of the three methods as the ball spin frequency is modulated by the inner and outer race defect frequencies which are visible in the frequency spectrum obtained by envelope analysis. | ||||||||||||||
GRAPHICAL USER INTERFACE |
||||||||||||||
| A Graphical User Interface (GUI) was developed using MATLAB Graphical User Interface Design Environment (GUIDE) in which, when the input is loaded through mat file, the frequency domain analysis is done and the results are plotted. The GUI developed is shown in Fig-7. In Fig-7, through the ‘Choose file’ list box, any mat file can be selected, whose drive end values are displayed in the ‘Data – DE’ list box. From the diagram ‘Bearing characteristic defect frequencies’, the characteristic defect frequencies can be observed. As soon as the file is loaded by the user, the rotational speed, RPM and Shaft frequency are displayed. In addition to that, the values of the three main characteristic defect frequencies, i.e., Inner race defect frequency, ball spin frequency and outer race defect frequency are also calculated and displayed in the GUI layout. Then, the user can select the method of frequency analysis, namely, FFT, Envelope Analysis, or Resampling. According to the choice of the method selected by the user, the graph will be plotted and the frequency spectrum is displayed. The GUI layout will be closed as soon as the ‘exit’ button is pressed. The GUI will be exported to a word document, when the user presses the ‘Export’ button and the word document is also opened. | ||||||||||||||
CONCLUSION |
||||||||||||||
| This paper demonstrate about the three methods in frequency domain analysis of a bearing namely, Discrete Fourier Transform (DFT), Envelope Analysis, and Resampling. It has been observed that, for inner race faulty bearings, resampling provides good results and for outer race faulty bearings, envelope analysis gives better results than resampling. For ball defective bearings, none of the methods give good results since it is modified by the inner and outer race defect frequencies. A Graphical User Interface (GUI) has been developed to demonstrate these techniques. | ||||||||||||||
Tables at a glance |
||||||||||||||
|
||||||||||||||
Figures at a glance |
||||||||||||||
|
||||||||||||||
References |
||||||||||||||
|