International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

BER Analysis of Various STBC Coding for MIMO Systems at Different Modulation Schemes

Mr. Ankit Pandit1 , Mr. S.J.Basha2 and Mr. K.K.Sharma3
  1. Student, Dept. of EC, LNCT Indore, Indore, India
  2. Professor, Dept. of EC, LNCT Indore, Indore, India
  3. Assistant Professor, Dept. of EC, LNCT Indore, Indore, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

This Paper shows the performance analysis of Bit Error Rate (BER) in MIMO system using STBC codes. We compare OSTBC scheme with different coding schemes viz; ABBA, Jafarkhani and Tarkoh at different modulation methods viz ; PSK, QAM. Zero-Forcing (ZF) , Minimum Mean Square Error (MMSE) equalization techniques are used for achieve full diversity.

Keywords
BER, MIMO, STBCs, ZF, MMSE

I . INTRODUCTION
An Improving demand for services for the wireless systems has turned wide variety into a valuable resource. Multiple- Input-Multiple-Output (MIMO) wireless channels have considerably higher capacities than traditional channels. Fading makes it extremely difficult for the receiver to recover the transmitted signal unless the receiver is provided with some form of diversity i.e. replicas of same transmitted signal with uncorrelated attenuation. In fact, diversity combining technology has been one of the most important contributors to reliable wireless communications. Consider transmit diversity by deploying multiple antennas at the base station. Moreover, in economic terms, the cost of multiple antennas at the base station can be amortized over numerous mobile users. Hence transmit diversity has been identified as one of the key contributing technologies to the downlinks of 3G wireless such as W-CDMA and CDMA2000. There are generally three categories of transmit diversity.
Feedback Scheme: This involves the feedback of channel state information (CSI, typically including channel gain phase information) from the receiver to transmitter in order to adapt the transmitter to the channel during the next transmission epochs. It is also commonly known as the “closed-loop” system.
Feedback forward Scheme: This involves the receiver making use of feed forward information sent by transmitter, such as pilot symbols, to estimate the channel, but no channel feedback information is sent back to the transmitter. It is also known as “open-loop” or “coherent” system.
Blind Scheme: This requires no feedback of CSI or feed-forward of pilots, and the receiver simply makes use of the received signal to attempt data recovery without knowledge of CSI. It is also known as the “non-coherent” system.
Space-Time Coding (STC) is technique that combines coding, modulation and signal processing to achieve diversity. The first STC proposed in the literature is Space-Time Trellis Code (STTC), which has a good decoding performance but decoding complexity that increases exponentially with transmission rate. In addressing the issue of decoding complexity of STTC, Space-Time Block Code (STBC) was subsequently proposed. Alamouti [1] discovered a remarkable STBC scheme for two transmit antennas. This scheme supports linear decoding complexity for Maximumlikehood (ML) decoding, which is much simpler than decoding of STTC. Alamouti’s scheme is very appealing in terms of implementation simplicity. Hence it motivates a Search for similar schemes for more than two antennas, to achieve full diversity level higher than two. As a result , Orthogonal Space-Time Block Codes (OSTBC) was introduced by tarkoh [2]. O-STBC is generalizations of the Alamouti’s scheme to arbitrary number of transmit antennas. It remains the property of having linear maximum- likehood with full transmit diversity.
In this paper we analyze the different space time coding style of MIMO system and related receiving algorithms (ZF, MMSE).The Paper is organized as follows: Section 2 describes the Alamouti STBC, ABBA, Jafarkhani, Tarkoh, Section 3 represents the equalization techniques-ZF, MMSE. Section 4 represents simulation results, the conclusions are offered in Section 5.

II.SPACE-TIME BLOCK CODES
Alamouti STBC
It is simple method for achieving spatial diversity with two transmits antennas. The scheme as follows Consider that we have a transmission sequence, for example
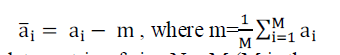image (1)
In normal transmission, we will be sending x1 in the first time slot, x2 in the second time slot, x3 and so on.
However, Alamouti suggested that we group the symbols into groups of two. In first time slot, send x1 and x2 from the first and second antenna. In the second time slot, send -x *2 and -x *1 from the first and second antenna. In third time slot, send x3 and x4 from the first and second antenna. In fourth time slot, send -x *3 and -x *4 from the first and second antenna and so on. Notice that though we are grouping two symbols, we still need two time slots to send two symbols. Hence, there is no change in data rate. This forms the simple explanation of the transmission scheme with Alamouti space time block coding. Alamouti scheme is an example of full rate full diversity complex Space-time block code. ABBA Code
Two Alamouti codes for two transmit antenna are used as a building blocks of the ABBA code for 4 transmit antennas:
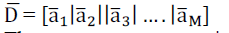image (2)
The equivalent virtual channel matrix HABBA results in:
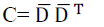image(3)
Applying a matched filter HH at the receiver, the non orthogonality of the ABBA code shows up in the Grammian Matrix GABBA :
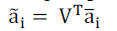image (4)
Where h2 = h1 2 + h2 2 + h3 2+ h4 2 is the channel gain and X is a channel dependent interference parameter:
image (5)
Our major limitation of the ABBA code is its loss of robustness in highly correlated channels, especially in the case when h1 = h2 = h3 = h4 which leads to collapse of all detection/decoding algorithms.
Jafarkhani Scheme
A lot of effort had been made to find orthogonal designs with highest rates in a systematic way. Therefore to reach a higher rate, one should change the structure of orthogonal code, e.g. relaxing one of the properties of an orthogonal design. For example we can think of designing a full-diversity rate one code that does not have the property single maximum likehood decoding. Increasing the order of complexity of decoding by one form separate decoding we get to pair-wise decoding: meaning that each two symbols should be detected independent of other pairs. The first such design was offered by jafarkhani in [3] as the following matrix:
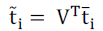image (6)
Where,
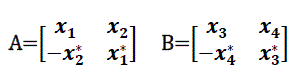image
The minimum rank of the A(C, E) is two for C ≠ E matrices. The design is called a quasi orthogonal Space-time block code. The reason is that in the design each column of the generator matrix is orthogonal to all the others except one, and so the name chosen Orthogonal.
The minimum rank of the A(C, E) is two for C ≠ E matrices. The design is called a quasi orthogonal Space-time block code. The reason is that in the design each column of the generator matrix is orthogonal to all the others except one, and so the name chosen Orthogonal.
A Space-time block code is defined by m x n transmission matrix GT. The entries of the matrix GT are linear combinations of the variables x1, x2...xk and their conjugates. The number of transmission antennas is n and we usually use it to separate different code to each other. For example, GT2 represents a code which utilizes two transmit antenna and is defined by:
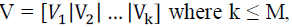image (7)
We assume that transmission at the baseband employs a signal constellation A with 2b elements. At time slot 1, kb bits arrive at the encoder and select constellation signals s1, s2... ... ...sk. Setting xi = si for i=1, 2.......k in GT we arrive at a matrix C with entries linear combinations of s1, s2... ... ...sk and their conjugates. So, while GT contains indeterminates x1, x2... ... ...xk C contains specific constellation symbols (or their linear constellations) which are transmitted from n antennas for each kb bits as follows. If cti represents the element in the tth row and the ith column of C, the entries cti i=1,2.............n are transmitted simultaneously from transmit antennas 1,2................m at each time slot 1,2.............m. So, ith column of C represents the transmitted symbols from the ith antenna and the tth row of C represents the transmitted symbols at time slot t note that C is basically defined using GT and the orthogonality of GT’s columns allows a simple decoding scheme which will be explained in the sequel. Since m time slots are used to transmit k symbols, we define the rate R of the code to be R= k/p . For example, the rate of GT2 is one. In this work, we consider the performance of the following rate half space-time block codes:
image (8)
image (9)
Proposed Scheme
Our proposed space-time block code is defined by m x n OSTBC Matrix T. The entries of the matrix T are linear combinations of variables x1, x2... ... ...xk and their conjugates T. Represents a code which utilizes two transmit antennas and is defined by:
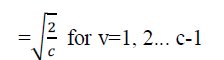image (10)

III. RECEIVING ALGORITHM
Zero-Forcing
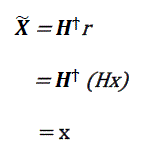Zero-Forcing technique is the simplest MIMO detection technique, where filtering matrix is constructed using the ZF performance based criterion. The drawback of ZF scheme is the susceptible noise enhancement and loss of diversity order due linear filtering [4]-[5] ZF can be implemented by using the inverse of channel matrix H to produce the estimate of transmitted vector image
image (11)
Where (.)ϯ denotes the pseudo-inverse. But when the noise term is considered, the post processing signal is given by:
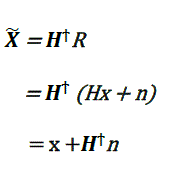image (12)
With the addition of the noise vector, ZF estimate, i.e. x- consists of the decode vector x plus a combination of the inverted channel matrix and the unknown noise vector. Because the pseudo-inverse of the channel matrix may have high power when the channel matrix is ill-conditioned, the noise variance is consequently increased and the performance is degraded. To alleviate for the noise enhancement introduced by ZF detector, the MMSE detector was proposed, where the noise variance is considered in the construction of the filtering matrix G.
Minimum mean square error
Minimum mean square error (MMSE) approach alleviates the noise enhancement problem by taking into considerations the noise power when constructing the filtering matrix using the MMSE performance based criterion. The vector estimates produced by an MMSE filtering matrix becomes:
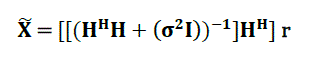image (13)
Where σ2 is noise variance . The added term ( 1 /SNR = σ2 , in case of unit transmit power) offers a trade of between the residual interference and the noise enhancement .Namely, as the SNR grows large, the MMSE detector converges to the ZF detector, but a low SNR it prevents the worst Eigen values from being inverted. At low SNR, MMSE becomes Matched filter
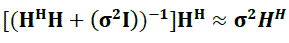image (14)
At high SNR , MMSE becomes ZF
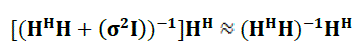image (15)

CONCLUSION
To achieve transmit diversity, various STBC codes has been implemented. Our proposed work achieves full diversity under the equalization techniques: Zero-Forcing (ZF) and Minimum Mean Square Error (MMSE). BER measurement shows the performance analysis of MIMO system is better in MMSE equalization at 4-PSK.

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
 
Figure 1 Figure 2 Figure 3
Figure 5 Figure 6 Figure 7
 

References