ISSN: 2319-9873
ISSN: 2319-9873
Hussein JA1*, Mazlan AW1 and Hasanen MH2
1Department of Mechanical Engineering, University Technology, Malaysia
2Machine and Mechanical Department, University of Technology, Baghdad, Iraq
Received date: 02/11/2015 Accepted date: 16/11/2015 Published date: 25/11/2015
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
In this paper, three-dimensional finite-volume numerical procedure has been used to solve the convective heat transfer coefficient (CHTC) and temperature distribution for two different geometries of internal room with side heated surfaces. A model room having the size of 80×60×60 cm dimensions is considered in this simulation. The temperature field is determined for various combinations of air-change per hour (5, 10, 15 and 20) and geometrical parameters to show some of the flow field characteristics.
Convective flow, CHTC, Temperature field, ACH.
Numerous theoretical and experimental expressions aiming at modeling the convective heat exchange of buoyancy-driven flows along vertical surfaces have been proposed. Ste´phane Fohanno [1] developed a modeling of convective heat transfer from interior vertical building surfaces subject to a uniform heat flux density. A simplified relation giving the average convective heat transfer coefficient as a function of the wall height and the wall heat flux density was proposed in order to be readily used in building simulation. Lari [2] studied combined heat transfer of natural convection and radiation in a 2D square cavity. The continuity, momentum and energy equations were solved by a finite volume method to obtain the temperature, velocity and heat flux distributions inside the participating medium. The heat transfer and flow characteristics of the cavity were analyzed at a broad range of Rayleigh numbers (102–106) and optical thicknesses (0–100). The results showed that the variation in radiative Nusselt number with optical thickness is several times larger than that of convective Nusselt number at the same Ra. Refet Karadag [3] determined the relation between radiative and convective heat transfer coefficient at the ceiling for a cooled ceiling room of which floor surface is isolated. The room dimensions were dimensions (3 × 3 × 3, 4 × 3 × 4 and 6 × 3 × 4 m) and thermal conditions (Tc = 0-25ºC, Tw = 28-36ºC). The results showed that the ratios of radiative heat transfer coefficients to convective heat transfer coefficients increases as the temperature differences increase. Petter Wallenten [4] measured the convective heat transfer coefficient at an outer ambient wall with a window exposed to natural climate in a room with and without furniture. The convective heat transfer was calculated as the difference between the heat flow through the building element and the calculated long-wave radiation. Tref was chosen as the vertical average in the middle of the room. A flow responsive method was used by Ian Beausoleil-Morrison [5] to advance the modelling of convective heat transfer at internal building surfaces. The algorithm dynamically controls the modelling of convection by assigning appropriate equations to each internal surface each timestep of the simulation. A new approach using ESP-r simulations was developed by Ian Beausoleil-Morrison [6] to demonstrate the mixed convection within mechanically ventilated rooms. ESP-r simulations performed with the mixed flow model indicate that the prediction of heating and cooling loads is highly sensitive to the treatment of surface convection. Francesco Causone [7] evaluated the heat transfer coefficients between radiant ceiling and room in typical conditions of occupancy of an office or residential building. In experimental results, a little higher average value of the total heat transfer coefficients was found of about 13.2 W m-2 K-1, for a cooled ceiling, compared to 11 W m-2 K-1 from the literature.
The fundamental set of equations that govern the flow of a fluid are derived from Newton's second law. The equations are called the Navier-Stokes equations, and for incompressible fluid the full instantaneous equations take the form:
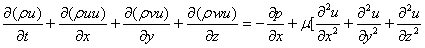 (1)
(1)
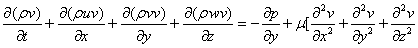 (2)
(2)
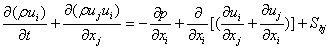 (3)
(3)
Where: (u,v and w) are the stream wise, lateral and vertical velocity components respectively,( x, y and z ) are the corresponding directions to the velocity components, μ is the fluid viscosity, ρ is the fluid density, p is the pressure.
It is more compact to write equation (1) to (3) in Cartesian tensor notation as:
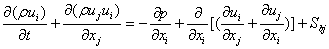 (4)
(4)
Where the suffixes i and j represent the three-co-ordinate direction upon expansion back to equations (1) to (3), Sbj are buoyancy source or sink terms and t is the time.
The conservation equations governing the dispersion of certain scalar properties of the flow, such as enthalpy temperature, turbulence kinetic energy K or turbulence dissipation rate ε , have similarity of form. They can therefore be represented by a single differential equation for some general scalar property ( Φ ) as follows:
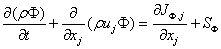 (5)
(5)
Where SΦ represents a source or sink for Φ , and J Φ,j is the diffusion in j −direction. The form of the latter flux will be discussed below. The scalar property flux J Φ,j, in equation (5) can be related to gradient of velocity components and scalar properties respectively. In constant-property flows this constitutive relation is as follows [8]:
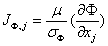 (6)
(6)
Where μ and σΦ are the dynamic viscosity and Prandtl /Schmidt number of fluid respectively.
Predication of air flow and convective heat transfer within an enclosure were performed numerically by solving the conservation laws which expressed in terms of elliptic partial differential equations by an iterative method. The independent variable of the problem are the three-component (x,y,z) of Cartesian Co-ordinate system. The main dependent variables are the velocity components ( u,v,w), pressure (p), temperature (T), turbulent kinetic energy (K) and its dissipation rate (ε ).By using a line-by-line solution technique in conjunction with a tri-diagonal matrix algorithm (TDMA), all dependent variables were solved, and a three-dimensional block adjustment procedure also applied in a line-by-line manner was employed to ensure continuity. The hybrid difference scheme is used in the convective terms and the integrated source term is linear zed. Both these practices are widely used to enhance numerical stability. A grid of non-uniform intervals is employed within the calculation domain in (x), (y) and (z) directions with the grid nodes concentrated near the walls and inlet and outlet grill.
The boundary conditions of the solid boundary which is used in the solution for the present problem is that no-slip condition is applied on the velocity at all six walls, and friction is calculated by invoking ''wall-function ''.
Numerical analysis based on finite volume method is used to solve three dimensional unsteady flows for two different geometries of internal room with side heated surfaces. A model room having the size of 80×60×60 cm dimensions with two different air source position is considered in this simulation as shown in Figure 1. The convective heat transfer coefficient and temperature distribution for room with two different air source positions are investigated.
Figure 2 shows the variation of the heat transfer coefficients with the temperature difference in geometry (a) at the 5 ACH for different wall temperatures. It can be seen from the figure that heat transfer coefficients increase proportional to the wall temperatures. By using of the Figure, a new correlation for the heat transfer coefficient has been developed as: CHTC=0.163*(Theater-Tinlet)1.136.
Influence of air change per hour (ACH) on the temperature profile is considered at X = 0.0225 and X=0.5725 m for two different geometries of internal room with side heated surfaces. In case of the air source position near the heated wall (geometry a), the warm air can reach lower levels of temperature 21ºC at 20 ACH in X= 0.0225 m as shown in Figure 3. As expected, the temperature in the central region of X= 0.5725 m at 5 ACH assume low values about of 19ºC and the temperature distribution are close to the end of region at 20 ACH (Figure 4).
In case of the air source position far away from the heated wall (geometry b), as foreseen, the range of temperature within the region at X= 0.0225 m varies from 19ºC to 33ºC at 5 ACH and from 19ºC to 25ºC at 20 ACH as shown in Figure 5. In the other side, only the middle portion of the region at X=0.5725 m with 20 ACH is closed to the initial condition of 21ºC while the temperature distribution range occurs near the edges of region from 24ºC to 26ºC (Figure 6).
The current work presents a model to predict the convective heat transfer coefficient (CHTC) and temperature distribution in internal room with side heated surfaces. The temperature field is determined for various combinations of air-change per hour. From the results of program, the present computer program may be used to predict the flow patterns and the internal and external convection heat transfer coefficients for complex flows.
The authors declare that there is no conflict of interests.