ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Dr.M.Ramakrishnan1, R.Sujatha2, S.B.Sony Thangam3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
A robust hashing method is developed for detecting forgery in images including removal, insertion, replacement of objects, abnormal color modifications and for locating the forged area. The hash sequence is formed by concatenating both the global and local features of the image. The global features are based on Zernike moments representing the luminance and chrominance characteristics of the image. The local features are based on position and texture information of the salient regions in the image. Secret keys are generated from the biometric image. Keys are protected by passing it through the chaotic neural network. These keys are used in feature extraction and hash construction. The generated hash is sensitive to tampering and hence it is used for image authentication. The hash of test image is compared with the hash of a reference image. When the hash distance is greater than a threshold t1 and less than t2, the received image is judged as a fake. By decomposing the hashes the type of image forgery and location of forged areas can be determined.
Keywords |
||||||||||
| Global features, local features, Zernike moments, Chaotic Neural Network, Image authentication | ||||||||||
INTRODUCTION |
||||||||||
| With the widespread use of image editing software, ensuring credibility of the image contents has become an important issue. Image hashing is a technique that extracts a short sequence from the image to represent its contents, and therefore can be used for image authentication. In general, a good image hash should be reasonably short, robust to ordinary image manipulations, and sensitive to tampering. It should also be unique in the sense that different images have significantly different hash values, and secure so that any unauthorized party cannot break the key and coin the hash. Feature values are protected by passing it through the Chaotic Neural Network. Hashing could be done by using the local features and global features. Global features are generally short but insensitive to changes of small areas in the image, while local features can reflect regional modifications but usually produce longer hashes. | ||||||||||
| In the present paper, we propose a method combining advantages of both global and local features. The objective is to provide a reasonably short image hash with good performance, i.e., being perceptually robust while capable of detecting and locating content forgery. We use Zernike moments of the luminance/chrominance components to reflect the image‘s global characteristics, and extract local texture features from salient regions in the image to represent contents in the corresponding areas. Distance metrics indicating the degree of similarity between two hashes are defined to measure the hash performance. Two thresholds are used to decide whether a given image is an original/normally-processed or maliciously doctored version of a reference image, or is simply a different image. The method can be used to locate tampered areas and tell the nature of tampering, e.g., replacement of objects or abnormal modification of colours. The rest of the paper is organized as follows. In Section II Literature survey is described. In section III ,Zernike moments, salient region detection and texture features are briefly introduced. Section IV presents the proposed image hashing scheme, and describes the procedure of image authentication. Section V deals with forgery classification and localization. Section VI presents the experimental results. Section VI concludes the paper. | ||||||||||
LITERATURE SURVEY |
||||||||||
| Various image hashing methods have been proposed. Monga et al. [2] develop a two-step framework that includes feature extraction (intermediate hash) and coding of the intermediate result to form the final hash.In [3], Xiang et al. propose a method using invariance of the image histogram to geometric deformations. It is robust to geometric attacks, but cannot distinguish images with similar histograms but different contents. Tang et al. [4] develop a global method using nonnegative matrix factorization (NMF). Swaminathan et al. [5] propose an image hash method based on rotation invariance of Fourier-Mellin transform and present a new framework to study the security issues of existing image hashing schemes. Their method is robust to geometric distortions, filtering operations, and various content-preserving manipulations.Khelifi et al. [6] propose a robust and secure hashing scheme based on virtual watermark detection. The method is robust against normal image processing operations and geometric transformation, and can detect content changes in relatively large areas. In another work, Monga et al. [7] apply NMF to pseudo-randomly selected subimages. Because the final hash comes from the secondary image with NMF, their method cannot locate forged regions. In analyzing the NMFNMF method, Fouad et al. [8] point out that, among the three keys it uses, the first one for pseudo-randomly selecting several subimages is crucial. However, it can be accurately estimated based on the observation of image hash pairs when reused several times on different images. Lv et al. [9] propose a SIFT-Harris detector to identify the most stable SIFT key points under various content-preserving operations. The extracted local features are embedded into shape-context-based descriptors to generate an image hash. The method is robust against geometric attacks and can be used to detect image tampering. The performance is degraded when the detected key points from the test image do not coincide with that of the original. | ||||||||||
BRIEF DESCRIPTION OF USEFUL TOOLS AND CONCEPTS |
||||||||||
| A.Zernike Moments | ||||||||||
| Zernike moment of order n and repetition m of a digital image I(ρ,) is defined by | ||||||||||
| ` |
||||||||||
| where (ρ,) is a zernike polynomial of order n and repetition m. | ||||||||||
| in which n = 0,1….,0 ≤ |m| ≤ n, n-|m| is even and Rn,m(ρ) are real valued radial polynomials. Suppose α is a rotation angle and Zn,m and Zn,m (r) the ZM of the original and rotated images respectively, then | ||||||||||
| B.Salient Region Detection:A salient region in an image is one that attracts visual attention. According to [10 ], information in an image can be viewed as a sum of two parts: that of innovation and that of prior knowledge. The former is new and the latter redundant. The information of saliency is obtained when the redundant part is removed.Log spectrum of an image, L(f) , is used to represent general information of the image. Because log spectra of different images are similar, there exists redundant information in L(f).Let A(f) denote the redundant information defined as convolution between L(f) and an l×l low-pass kernel h1 : | ||||||||||
| We choose a threshold equal to three times of the mean of SM(x) to determine the salient regions. For example, Fig. 1(a) is an original image, (b) its saliency map, (c) the salient regions after thresholding , and (d) the image marked with three circumscribed rectangles of the largest connected salient regions. We will extract the image’s local features from these rectangles. | ||||||||||
| C.Texture features:Texture is an important feature to human visual perception. In [13 ] and [14 ], the authors propose six texture features relating to visual perception: coarseness, contrast, directionality, line-likeness, regularity and roughness. In this work, we use coarseness C1 and contrast C2 as defined below, plus skewness and kurtosis, to describe the texture properties.To evaluate coarseness around a pixel at (x,y),the pixels in its neighborhood sized 2k × 2k are averaged: | ||||||||||
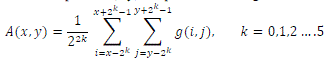 (5) (5) |
||||||||||
| Where g(i,j) is the gray level of pixel(i,j).At each point (x,y),difference between pairs of the average values of nonoverlapping neighborhoods on opposite sides of the pixel in horizontal and vertical directions are: | ||||||||||
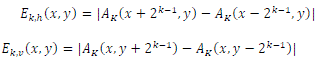 (6) (6) |
||||||||||
| For that point, find the size that leads to the highest difference value and call it Sopt(x,y). | ||||||||||
| Take average of Sopt over a region,,and call it coarseness of that region,C1.Contrast describes the degree of image brightness variation, calculated from variance 2 and the fourth order moment μ4 of the gray values within the region: | ||||||||||
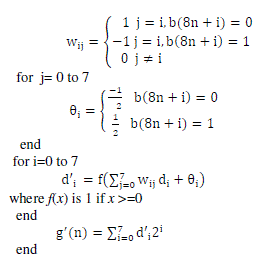 (8) (8) |
||||||||||
PROPOSED HASHING SCHEME |
||||||||||
| In this section, we describe the proposed image hashing scheme and the procedure of image authentication using the hash. The hash is formed from Zernike moments to represent global properties of the image, and the texture features in salient regions to reflect local properties. | ||||||||||
| A.Image Hash Construction | ||||||||||
| The image hash generation procedure includes the following steps, referring to Fig. 2. | ||||||||||
| 1) Preprocessing:The image is first rescaled to a fixed size F×F with bilinear interpolation, and converted from RGB to the YCbCr representation. Y and |Cb-Cr| are used as luminance and chrominance components of the image to generate the hash. The aim of rescaling is to ensure that the generated image hash has a fixed length and the same computational complexity. Small F leads to loss of fine details, while large F results in high computational complexity. We choose F=256 as an appropriate trade-off. | ||||||||||
| 2) Global Feature Extraction:Zernike moments of Y and |Cb-Cr| are calculated. Because shape features can be obtained from a small number of low frequency coefficients, the order n does not need to be large. We choose n=5.Further, since = , only (m ≥ 0) is needed.We do not use as it represents the average intensity. Table I lists the Zernike moment features from order 1 to order 5.Thus we have 11× 2=22 Zernike moments in total. Magnitudes of the Zernike moments are rounded and used to form a global vector, Z = ZY ZC . ach element in Z is no more than . secret key k1 is used to randomly generate a row vector X1 with 22 random integers in [0,255].The encrypted global vector Z is obtained as Z = (Z 1)mod 256]. | ||||||||||
| 3) Local Feature Extraction:K largest salient regions are detected from the luminance image Y .The coordinates of top left corner and width/height of each circumscribed rectangle are used to form a K- element vector p(k)(k=1, …..K),representing the position and size of each salient region. From the statistics based on 3000 images, more than 97% of the images have no more than 6 salient regions. For those having more than 6 salient regions, the total area of the 7th and smaller salient regions are less than 1.5% of the image areas. With larger K, fewer salient regions are missing but will lead to a longer image hash. For example, the percentage of images with no more than 7 salient regions is 99.5%. We choose K=6 as a reasonable trade-off. Local texture features of each salient region including coarseness C1 and contrast C2,skewness and kurtosis are computed and rounded to give a 6 element vector t(k) (k = 1, ,…6).If an image has less than 6 salient regions, the positions and texture features of the missing ones are set to zero. he position/size and texture vectors of all salient regions together form a local feature vector S = = p(1)…..p(6)t(1) ……t(6)],which contains 48 integers. A secret key K2 is used to randomly generate a row vector X2 containing random integers in 0, . n encrypted local vector S is then obtained by S= (S 2)mod 256]. | ||||||||||
| 4) Hash construction:The global and salient local vectors are concatenated to form an intermediate hash, namely = Z S , which is then pseudo randomly scrambled based on a secret key K3 to produce the final hash sequence H. Table II gives the constitution of an image hash of 70 integers. Since all integers are in the range of [0, 255], the hash is 70×8,560 bits long. | ||||||||||
| 5)Feature protection using Chaotic Neural Network:In triple key chaotic encryption method, 20 hexadecimal characters are entered as a session key. The binarisation of this hexadecimal key gives 80 bits. Some bits are extracted and some manipulations are performed on it to obtain the intermediate key. This intermediate key is combined with initial and control parameters to generate chaotic sequence. his is the concept of ‘ riple key’. In this, there is three step protection to the original image. User has to entered three keys to decrypt the image. | ||||||||||
| Algorithm | ||||||||||
| 1. Read the image. | ||||||||||
| 2. Determine the size and length of image. | ||||||||||
| 3. Converting two dimensional image vector in one dimensional image vector. | ||||||||||
| 4. Computing initial parameter from hexadecimal session key, . | ||||||||||
| It consists of 80 bits i.e. binary representation of hexadecimal key. | ||||||||||
| 5. X(1) = ( + + ) mod 1. | ||||||||||
| 6. Determine parameter μ. | ||||||||||
| 7. Generate the chaotic sequence x(1), x( ), (3)…..x(M) by the formula | ||||||||||
| x(n + 1) = mx(n) (1 – x(n)) Create | ||||||||||
| b(0), b(l), ..., b(8M – 1) from x(l), x(2),.... x(M) by the generating scheme that b(8m – 8)b(8m – 7)….. b(8m – 2) b(8m – l) … is the binary Representation of x(m) for m =1, ,….M. | ||||||||||
| 8. Weights and theta are decided | ||||||||||
| for i = 0 to 7 | ||||||||||
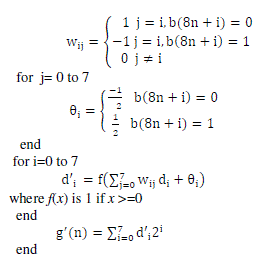 |
||||||||||
| B. Image Authentication | ||||||||||
| In image authentication, the hash of a trusted image,H0, is available and called the reference hash. The hash of a received image to be tested,H1 , is extracted using the above method. These two hashes are compared to determine whether the test image has the same contents as the trusted one or has been maliciously tampered, or is simply a different image. Here, two images having the same contents (visual appearance) do not need to have identical pixel values. One of them, or both, may have been modified in normal image processing such as contrast enhancement and lossy compression. In this case, we say the two images are perceptually the same, or similar. The image authentication process is performed in the following way. | ||||||||||
| 1)Feature Extraction:Pass the test image through the steps as described in Section A to obtain the intermediate hash without encryption, namely H1 =[Z1 P1 T1]. | ||||||||||
| 2)Hash Decomposition:With the secret keys K1,K2 andK3 , restore the intermediate hash from the reference hash to obtain H0 =[Z0 P0 T0] , which is a concatenated feature sequence of the trusted image. Decompose it into global and local features. | ||||||||||
| 3)Salient Region Matching: Check if the salient regions found in P1 of the test image match those in P0 of the trusted image. If thematched areas of a pair of regions are large enough, the two regions are considered as being matched. Reshuffle the texture vectors by moving the matched components in each of the texture vector pair to the left-most and, for notational simplicity, still call them T0 and T1. For example, if there are three salient regions in the reference image and two in the test image,T0=[t0 (1) t0 (2) t0 (3) 0 0 0],T1=[t1 (1) t1 (2) 0 0 0 0].The first two pairs of subvectors in T0 and T1 may either be matched or unmatched. The vectors P0 and P1 are reshuffled accordingly. | ||||||||||
| 4)Distance calculation: We use a distance between hashes of an image pair as a metric to judge similarity/ dissimilarity of the two images. To define the hash distance, a feature vector V is formed by concatenating the global feature vector Z and the reshuffled texture feature vector T , namely V=[Z T] . The vector does not contribute to the distance calculation but will be used to locate forged regions. The hash distance between the test image and the reference is the Euclidean distance between V0 and V1: D=|| V1 – V0 ||.To minimize the influence of saliency detection inaccuracy,we omit T in calculating the hash distance for similar images: D=||Z1 – Z0||=DG.Having defined the hash distance, we can use it first to distinguish similar and dissimilar images according to a threshold 1. If DG ≤ 1, the two images are said to be similar, otherwise the images are dissimilar. We then need to further determine whether the test image is a tampered version of the reference image, or simply a different one. To do so, compare the distance with a second thresholds 2. The test image is judged as tampered if D ≤ 2. Otherwise it is a completely different image. | ||||||||||
| C)Determination of thresholds: To determine a threshold for differentiating two sets of data, A and B, we need to know the probability distribution functions (PDF) of samples taken from these data sets. The chi-square test [15] is used for the purpose. Assume that the data satisfy one of several common distributions: Poisson, lognormal, and normal, and apply the chi-square test to find which is the closest. The statistic X2 is calculated as Σ where v is the number of trials, the frequency of a distance being i(i=0,1….L) , and pi is probability of the distance being calculated from the tested PDF. The PDF is the one that produces the smallest X2 value. For simplicity, we choose the horizontal coordinate of the two PDF curves’ intersection as the threshold in the present work irrespective of the particular PDF shapes and the costs of different types of errors. | ||||||||||
FORGERY CLASSIFICATION AND LOCALIZATION |
||||||||||
| Having found that a test image is a fake, the next job is to locate the forged region and tell the nature of forgery. Four types of image forgery can be identified: removal, insertion and replacement of objects, and unusual color changes. Forgery classification and localization are performed as follows, and schematically illustrated in Fig. 4. Decode and into components representing global and local features, and find the number of matched salient regions and the numbers of salient regions in the reference and test images,N0 and N1. | ||||||||||
| 1) If N0 > N1 =R , some objects have been removed from the received test image. Positions of the missing objects are located by comparing the saliency indices. | ||||||||||
| 2) If N1 > N0 =R, the test image contains some additional objects whose positions are located by comparing the saliency indices. | ||||||||||
| 3) If N1 = N0 =R , check the luminance and chrominance components in the Zernike moments and calculate the following distances:δZC= ||ZC1 –ZC0||, δZY= ||ZY1 – ZY0||.If δZC is greater than δZY by a threshold C , the test image contains substantial color changes with respect to the reference image while the luminance changes are considerably smaller. Thus the test image is judged as being tampered with unusual color modifications. The threshold is chosen as 5 based on experiments of 50 image pairs. | ||||||||||
| 4) If N1 = N0 =R and (δZC – δZY) is less than c , the test image contains replaced objects because in this case lluminance changes are dominant. Calculate the distance between the texture feature vectors of each salient region.The k-th salient region having maximal value is recognized as being replaced. | ||||||||||
| 5)If N0 > R and N1 > R,some of the salient regions are not matched.Mark the mismatched salient regions in the test image as being tampered. | ||||||||||
EXPERIMENTAL RESULTS |
||||||||||
| A few examples of forgery detection are shown in fig. 5.The table gives the original and forged images,salient regions and detection results. | ||||||||||
| Original image Forged image Salient region Detection result | ||||||||||
| In the third column from the left, the solid purple rectangles indicate matched salient regions; the dashed blue rectangles are salient regions that only exist in the forged images but not in the original; and the dash-dotted yellow rectangles show regions where salient regions exist in the original but disappear after forgery. The rectangles in the fourth column indicate the detected forged regions. In the table, the first two rows are examples of object removal, the third and fourth rows object insertion, and the last two rows object replacement. Fig. 6 shows examples of unusual color changes, in which (a) and (c) are original images, and (b) and (d) forged ones. | ||||||||||
CONCLUSION |
||||||||||
| In this paper, an image hashing method is developed using both global and local features. The global features are based on Zernike moments representing the luminance and chrominance characteristics of the image as a whole. The local features include position and texture information of salient regions in the image. Keys are used in both feature extraction and hash generation. Feature values are protected by passing through Chaotic Neural Network.Hashes produced with the proposed method are robust against common image processing operations including brightness adjustment, scaling, small angle rotation, JPEG coding and noise contamination. Collision probability between hashes of different images is very low. The method described in this paper is aimed at image authentication. The hash can be used to differentiate similar, forged, and different images. At the same time, it can also identify the type of forgery and locate fake regions containing salient contents. In the image authentication, a hash of a test image is generated and compared with a reference hash previously extracted from a trusted image. When the hash distance is greater than the threshold 1 but less than , the received image is judged as a fake. By decomposing the hashes, the nature of image forgery and locations of forged areas can be determined. | ||||||||||
Figures at a glance |
||||||||||
|
||||||||||
References |
||||||||||
|