ISSN: 2319-9873
ISSN: 2319-9873
Department of Electrical Engineering, Urmia Branch, Islamic Azad University, Urmia, Iran
Received: 01/01/2013; Revised: 04/02/2013; Accepted: 07/02/2013
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
This paper proposes a simple Shape-Based Retrieval (SBR) systems, which a novel feature-based shapes descriptors using Radon composite features by using statistical and spectral analysis are used in this system, Instead of analyzing shapes directly in the spatial domain. SBR systems employ Texture as primary feature with shape secondary features. Till now systems exploit spatial features. None of the available systems combines all features, texture, and shape for retrieval. Moreover relatively few systems use Radon Transform in texture extraction features, despite the widely acclaimed efficiency. The proposed system uses combination of integrated first and second moments of radon transformed image features, and Hue Moments features of the regions as shape features then Linear Discriminated Analysis (LDA) are applied for decreasing the dimension of feature vector and non linear combination of vector dimensions for generating optimum features. Experiments demonstrate that proposed novel feature-based shapes system provides a higher degree of retrieval and are compared with several state-of-the-art approaches.
Shape Classification, Descriptor, Retrieval, Radon Transform, LDA.
A retrieval system is a system for searching and retrieving images from a large database of digital images. The most common method of image retrieval utilize some method of annotation such as keywords, or descriptions to the images so that retrieval can be performed over the labels. Unfortunately manual annotation is time consuming, laborious and expensive. Shape based retrieval (SBR) describes the process of retrieving desired images from the image database on the basis of syntactical image features. Research comprise of systems such as [1,2,3]. The features most often used include texture, shape information and multi-resolution pixel intensity transformations such as wavelets or multi-scale Gaussian filtering [4] and in old and traditional systems low level features extraction method are used in this method always semantic gap are sensed so, for eliminating semantic gap combinational features such as textural and shape features are used simultaneously and for increasing the percentage of retrieval some nonlinear and linear feature and vector dimension are evaluated.
The organization of this paper as follows: In Section II, we provide a brief review of Radon transform equations.
Section III gives the Feature Extraction. In Section IV, the retrieval strategy is introduced, and the results of the experiments and extensive comparisons are performed with several state-of-the-art algorithms. Conclusions are drawn in Section V.
An image is represented by a function s(x,y), and the image can be determined by a set of projections along lines taken at different angles. Therefore, the Radon transform is defined as:
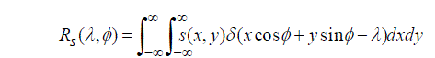 (1)
(1)
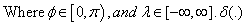 represents the Dirac delta-function
represents the Dirac delta-function
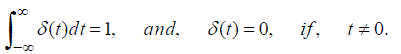 (2)
(2)
For shape analysis, image represents a binary planar shape. so, it is interest to consider the case in which the general s(x,y)is replaced by a particular function sD(x,y) where
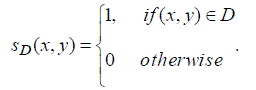 (3)
(3)
The definition corresponds to the transformation of a binary shape image where D is its domain. The contributions to the integral of Rs will have nonzero values when the argument of the delta function evaluates to zero. The Radon transform describes the length intersection of all the intensity line with the function of sD for all the 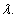 The transform obtains an array of
The transform obtains an array of 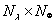 rectangular cells, corresponding to the computed values of
rectangular cells, corresponding to the computed values of 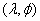 [5]. Figure 1 shows orginal image and its radon transform.
[5]. Figure 1 shows orginal image and its radon transform.
Radon transform is usually used to model the process of acquiring projections of the original objects using X-rays and of reconstructing the original object from the projections. However, the Radon matrix cannot directly represent the shape structures, because it is not invariant to geometrical transformations, and to measure the similarity between two shapes using the Radon matrix directly is not suitable [5].
Today, the most commonly used methods for texture feature description are statistical and transform based methods. In the present work a transformed based method is used. The state-of-the-art in transformed based texture feature extraction uses Radon. This is due to research [5] that Radon features is invariant to rotation and scaling so features which are generated are so valuable features [5] showed that Radon features acts better than using pyramid structured, tree-structured wavelet transform features and multi-resolution simultaneous autoregressive model. Radon Transform was addressed by choosing the parameters to be set of frequencies and orientations that cover the entire spatial frequency space so as to capture texture information as much as possible. In our approach after achieving transformed of image we extract first and second moments from array of transformed image that textural feature vector dimension will be 181*1 for each image, that is 180 for standard of deviation and 1 for mean value. For example if we have 1400 image in our database the size of feature database matrix will be 181*1400. By assuming spatial homogeneity of texture regions the mean and the std. deviation of the magnitude of the transformed coefficients was computed according to:
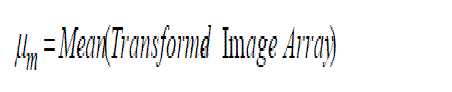 (4)
(4)
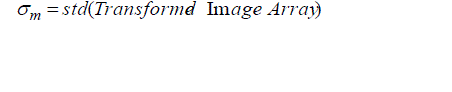 (5)
(5)
Parameter m is between 0:1:179 that it fluctuate for different value of thetas. Finally, the textural feature vector for each image is constructed using the computed values for the mean μmn and std. deviation σm according to:
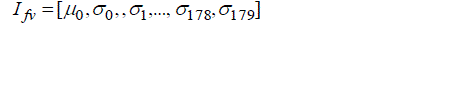 (6)
(6)
For each image of database we repeat the process to get the textural features database. At next section shape features are calculated and add to these textural features vector.
Shape of an object is the characteristic surface configuration as represented by the contour. Shape recognition is one of the modes through which human perception of the environment is executed. In our proposal the shape features are extracted using Hue Moments. Hu invariants moment are a set of nonlinear functions, which are invariant to translation, scale, and orientation and are defined on normalized geometrical central moments [6]. Hu introduced seven moment invariants based on normalized geometrical central moments up to the third order. Since the higher order moment invariants have resulted higher sensitivity, a set of eight moment invariants limited by order less than or equal to four seems to be proper in most applications. Having normalized geometrical central moments of order four and the lesser ones, seven moment invariants (ø1 -ø8 ) introduced by Hu and can be computed using equation 11.
Geometrical moment of order (p+q) for a two dimensional discrete function like image is computed by using (7). If the image can have nonzero values only in the finite part of xy plane; then moments of all orders exist for it [6].
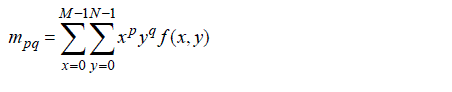 (7)
(7)
Where f(x, y) is image function and M, N are image dimensions. Then, by using (8) geometrical central moments of order equal to (p+q) can be computed.
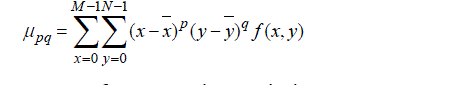 (8)
(8)
Where 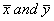 are gravity center of image and are calculated by using (9). Actually by image translation to coordinate origin while computing central moments, they become translation invariant.
are gravity center of image and are calculated by using (9). Actually by image translation to coordinate origin while computing central moments, they become translation invariant.
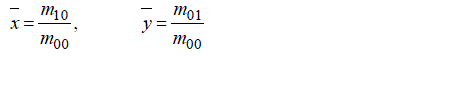 (9)
(9)
Note that in a binary image, m00 = µ00 is count of foreground pixels and has direct relation to image scale, therefore central moments can become scale normalized using (10).
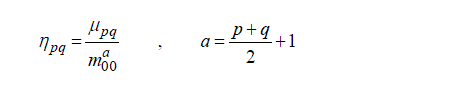 (10)
(10)
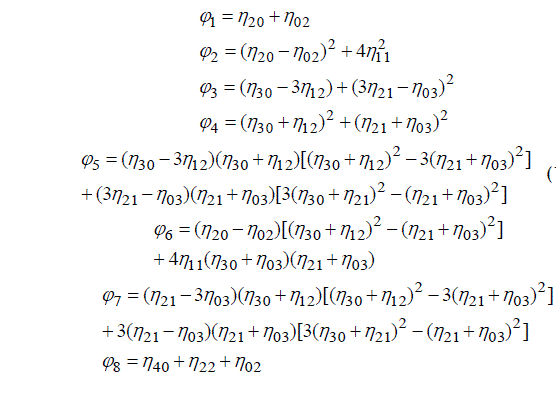 (11)
(11)
After calculating Hu moments, this Hu feature vector (12) will be add to previous textural features now dimension of combined feature is 189*1,equation (13), then LDA algorithm is applied for extracting optimum features, at next section method will be completely explained.
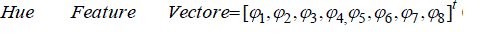 (12)
(12)
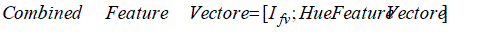 (13)
(13)
The LDA is a well-known feature extraction technique in the multivariate analysis. It is an orthogonal transformation of the coordinate in which the data is described. The LDA tries to find a lower dimensional subspace to describe the original dataset while preserving the information as much as possible, so a new k-dimensional dataset will be produced, where k is smaller than previous dataset dimensions.
Practically, the LDA algorithm proceeds by first computing the mean of vectors and then subtracting them from this mean value. The total class the covariance matrix is calculated and its eigenvectors and Eigen-values are founded. The eigenvectors that correspond to the k of largest Eigen-values are retained, and the input vectors are projected onto the eigenvectors to give the components of the transformed vectors in the k-dimensional space. Hereafter, the vectors are represented by a linear combination of eigenvectors. The dimensionality reduction error indicates that the introduced error can be eliminated by choosing an appropriate dimensionality reduction.
Have the above feature descriptors as the basis for SBR system, we proceed to develop the system. In doing so the user can select and image and then select whether to use any of the individual features alone or combined together using the weights in the upper right corner LDA [7].
Now proposed system has used LDA algorithm for decreasing combined features dimension for two reasons:
1) Decreasing volume of memory for feature dataset.
2) Increasing speed of retrieval or less complexity.
By using LDA algorithm dimension of Combined feature vectors reduced from 189 to 80 which we will have up to 30% percentage more volume of memory, that is in large image sets big memory are used for keeping feature dataset therefore using such a technique less memory will be occupied. Size of optimized features is 80.
While decreasing dimension of extracted Feature will increase speed of retrieval because less time is need for calculation distance among optimized features. It is important to add that Euclidean distance has used for retrievaling the images from database because of simplicity and less time consumption in retrieval block.
A series of experiments are performed to evaluate the proposed approach. The first group performs on a widely used dataset the MPEG-7 CE-1 part B database [5], which is broadly used to measure performances of similarity-based retrieval. This dataset consists of 1400 shapes: 70 groups, 20 similar shapes per group (Fig. 2).
Fig. 3 shows the precision–recall diagram of the 3 shape descriptors. It can be seen that Zernike moments perform better than shape signature, and Combinational Radon based features and Hue moments produces most accurate results. It is because proposed method makes full use of the information involved in a shape region and the extracted features have a high degree of discrimination power. The performance of the proposed system is assessed using recall curve with the help of randomly selected query-images (Fig4). In assessing the performance of the proposed system a series of query-images are given to the system and then one precision curve is computed per query.
In this paper a SBR system has been presented. The system puts emphasis on texture, which is the primary feature, and less emphasis on shape features. First and second moments features are generating from transformed radon image and Hue Moments are used as shape features were incorporated into the SBR system and after that LDA algorithm is applied to database features for extracting optimum features. The results show that the combination of all features provides higher performance than other traditional methods.